2018-2019学年初中数学人教版八年级下册 19.2一次函数 同步练习
试卷更新日期:2019-06-18 类型:同步测试
一、选择题
-
1. 下面函数图象不经过第二象限的为( )
A、y=3x+2 B、y=3x-2 C、y=-3x+2 D、y=-3x-22. 若正比例函数的图象经过点(-1,2),则这个图象必经过点( )A、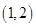 B、
B、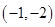 C、
C、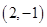 D、
D、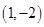 3. 一次函数 图象上有两点A 、B , 则 与 的大小关系是( )
3. 一次函数 图象上有两点A 、B , 则 与 的大小关系是( )
A、 B、 C、 D、4. 一次函数y=(m﹣2)x+3的图象如图所示,则m的取值范围是( )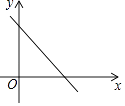 A、m<2 B、0<m<2 C、m<0 D、m>25. 如图,已知:函数y=3x+b和y=ax﹣3的图象交于点P(﹣2,﹣5),则根据图象可得不等式3x+b>ax﹣3的解集是( )
A、m<2 B、0<m<2 C、m<0 D、m>25. 如图,已知:函数y=3x+b和y=ax﹣3的图象交于点P(﹣2,﹣5),则根据图象可得不等式3x+b>ax﹣3的解集是( )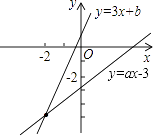 A、x>﹣5 B、x>﹣2 C、x>﹣3 D、x<﹣2
A、x>﹣5 B、x>﹣2 C、x>﹣3 D、x<﹣2二、填空题
-
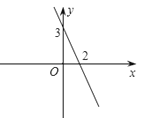
6. 一次函数y=﹣2x+4的图象与x轴交点坐标是 , 与y轴交点坐标是 , 图象与坐标轴所围成的三角形面积是 .7. 一次函数y=kx+b的图象如图所示,当y>0时,x的取值范围是
 8. 一次函数y=(m﹣1)x+m2的图象过点(0,4),且y随x的增大而增大,则m= .9. 已知直线y=kx+b与x轴的交点坐标是(2,0),则关于x的方程kx+b=0的解是x=.
8. 一次函数y=(m﹣1)x+m2的图象过点(0,4),且y随x的增大而增大,则m= .9. 已知直线y=kx+b与x轴的交点坐标是(2,0),则关于x的方程kx+b=0的解是x=.
10. 若函数y=(a﹣3)x|a|﹣2+2a+1是一次函数,则a= .11. 如图,已知A地在B地正南方3千米处,甲乙两人同时分别从A,B两地向正北方向匀速直行,他们与A地的距离S(千米)与所行的时间t(小时)之间的函数关系图象如图所示的AC和BD给出,当他们行走3小时后,他们之间的距离为千米.
三、解答题
-
12. 设y﹣5与x+3成正比例,且当x=﹣2时,y=8.求y与x之间函数关系式.13. 已知,若函数y=(m﹣1)+3是关于x的一次函数
(1)求m的值,并写出解析式.
(2)判断点(1,2)是否在此函数图象上,说明理由.
14. 如图,已知一次函数y1=(m﹣2)x+2与正比例函数y2=2x图象相交于点A(2,n),一次函数y1=(m﹣2)x+2与x轴交于点B.(1)求m、n的值;
(2)求△ABO的面积;
(3)观察图象,直接写出当x满足什么条件时,y1>y2 .
 15. 小明从家骑自行车出发,沿一条直路到相距2400m的邮局办事,小明出发的同时,他的爸爸以96m/min速度从邮局同一条道路步行回家,小明在邮局停留2min后沿原路以原速返回,设他们出发后经过t min时,小明与家之间的距离为s1 m,小明爸爸与家之间的距离为s2 m,图中折线OABD、线段EF分别表示s1、s2与t之间的函数关系的图象.
15. 小明从家骑自行车出发,沿一条直路到相距2400m的邮局办事,小明出发的同时,他的爸爸以96m/min速度从邮局同一条道路步行回家,小明在邮局停留2min后沿原路以原速返回,设他们出发后经过t min时,小明与家之间的距离为s1 m,小明爸爸与家之间的距离为s2 m,图中折线OABD、线段EF分别表示s1、s2与t之间的函数关系的图象.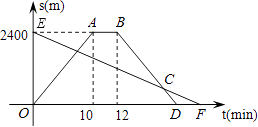 (1)、求s2与t之间的函数关系式;(2)、小明从家出发,经过多长时间在返回途中追上爸爸?这时他们距离家还有多远?16. 我省是水资源比较缺乏的省份之一,为了加强公民的节水意识,合理利用水资源,各地采用价格调控等手段达到节约用水的目的,其中,某市规定如下用水收费标准:每户每月的用水量不超过6立方米时,水费按每立方米a元收费;超过6立方米时,不超过的部分每立方米仍按a元收费,超过的部分每立方米按c元收费.
(1)、求s2与t之间的函数关系式;(2)、小明从家出发,经过多长时间在返回途中追上爸爸?这时他们距离家还有多远?16. 我省是水资源比较缺乏的省份之一,为了加强公民的节水意识,合理利用水资源,各地采用价格调控等手段达到节约用水的目的,其中,某市规定如下用水收费标准:每户每月的用水量不超过6立方米时,水费按每立方米a元收费;超过6立方米时,不超过的部分每立方米仍按a元收费,超过的部分每立方米按c元收费.该市今年3、4两月使用水量和水费如下表所示:
月份
用水量(立方米)
水费(元)
3
5
7.5
4
9
27
设该户每月用水量为x(立方米),应交水费y(元).
(1)、求a、c的值,并写出用水量不超过6立方米和超过6立方米时,y与x的函数关系式;(2)、该户5月份的用水量为8立方米,求该户5月份的水费是多少元?