浙江省温州市瓯海区2019年数学中考二模试卷
试卷更新日期:2019-06-17 类型:中考模拟
一、单选题
-
1. 给出四个数0, ,π,﹣1,其中最小的是( )A、0 B、 C、π D、﹣1
-
2. 为了鼓励学生课外阅读,学校公布了“阅读奖励”方案,征求了所有学生的意见,根据赞成、反对、无所谓三种意见的人数之比画出扇形统计图,图中α的度数为( )
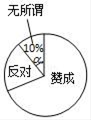 A、36° B、20° C、10° D、无法确定
A、36° B、20° C、10° D、无法确定 -
3. 式子 有意义的x的取值范围是( )A、 且x≠1 B、x≠1 C、 D、 且x≠1
-
4. 如图是由几个相同的正方体搭成的一个几何体,从正面看到的平面图形是( )
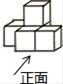 A、
A、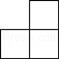 B、
B、 C、
C、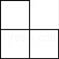 D、
D、
-
5. 若反比例函数y= (k≠0)的图象经过点P(2,﹣3),则该函数的图象不经过的点是( )A、(3,﹣2) B、(1,﹣6) C、(﹣1,6) D、(﹣1,﹣6)
-
6. 设a、b是两个整数,若定义一种运算“△”,a△b=a2+b2+ab,则方程(x+2)△x=1的实数根是( )A、x1=x2=1 B、x1=0,x2=1 C、x1=x2=﹣1 D、x1=1,x2=﹣2
-
7. 如图所示,已知AB∥CD∥EF,那么下列结论正确的是( )
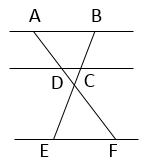 A、 B、 = C、 = D、 =
A、 B、 = C、 = D、 = -
8. 在平面直角坐标系中,若有一点P(2,1)向上平移3个单位或向左平移4个单位,恰好都在直线y=kx+b上,则k的值是( )A、 B、 C、 D、2
-
9. 已知AB是⊙O的弦,且AB= OA,则∠OAB的度数为( )A、30° B、60° C、120° D、150°
-
10. 若0<m<2,则关于x的一元二次方程﹣(x+m)(x+3m)=3mx+37根的情况是( )A、无实数根 B、有两个正根 C、有两个根,且都大于﹣3m D、有两个根,其中一根大于﹣m
二、填空题
-
11. 因式分解:9a2﹣12a+4=.
-
12. 抛掷一枚质地均匀的骰子1次,朝上一面的点数不小于3的概率是 .
-
13. 如图,D在BC边上,△ABC≌△ADE , ∠EAC=40°,则∠B 的度数为 .

-
14. 甲从A地到B地,去时步行,返回时坐车,共用x小时,若他往返都坐车,则全程只需 小时,若他往返都步行,则需小时.
-
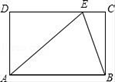
15. 如图,矩形ABCD中,点E在边DC上,且AD=8,AB=AE=17,那么tan∠AEB=.
-
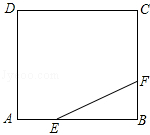
16. 如图,正方形ABCD的边长为3,点E,F分别在边AB、BC上,AE=BF=1,小球P从点E出发沿直线向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第一次碰到点E时,小球P所经过的路程为.
三、解答题
-
17.(1)、计算: ;(2)、化简并求值: ,其中 , .
-
18. 某县在一次九年级数学模拟测试中,有一道满分为8分的解答题,按评分标准,所有考生的得分只有四种情况:0分、3分、5分、8分.老师为了了解学生的得分情况与题目的难易程度,从全县9000名考生的试卷中随机抽取若干份,通过分析与整理,绘制了如下两幅不完整的统计图.
九年级数学质量检测一道解答题学生得分情况统计图

请根据以上信息解答下列问题:
(1)、该题学生得分情况的众数是.(2)、求所抽取的试卷份数,并补全条形统计图.(3)、已知难度系数的计算公式为 ,其中L为难度系数,X为样本平均得分,W为试题满分值.一般来说,根据试题的难度系数可将试题分为以下三类:当0≤L<0.5时,此题为难题;当0.5≤L≤0.8时,此题为中等难度试题;当0.8<L≤1时,此题为容易题.通过计算,说明此题对于该县的九年级学生来说属于哪一类? -
19. 尺规作图:
已知:∠AOB.
求作:射线OC,使它平分∠AOB.
作法:
①以O为圆心,任意长为半径作弧,交OA于D,交OB于E;
②分别以D、E为圆心,大于 DE的同样长为半径作弧,两弧相交于点C;
③作射线OC.
所以射线OC就是所求作的射线.
(1)、使用直尺和圆规,补全图形;(保留作图痕迹)(2)、完成下面的证明.证明:连结CE,CD.
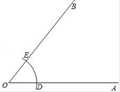
∵OE=OD,= , OC=OC,
∴△OEC≌△ODC(依据:),
∴∠EOC=∠DOC,
即OC平分∠AOB.
-
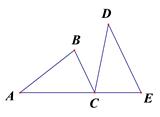
20. 如图,点C在线段AE上,BC∥DE,AC=DE,BC=CE.
求证:AB=CD.
-
21. 已知抛物线y=ax2+bx经过点A(﹣3,﹣3)和点P(m,0),且m≠0.
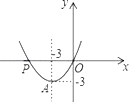 (1)、如图,若该抛物线的对称轴经过点A,求此时y的最小值和m的值.(2)、若m=﹣2时,设此时抛物线的顶点为B,求四边形OAPB的面积.
(1)、如图,若该抛物线的对称轴经过点A,求此时y的最小值和m的值.(2)、若m=﹣2时,设此时抛物线的顶点为B,求四边形OAPB的面积. -
22. 如图,已知AB是半圆O的直径,OC⊥AB交半圆于点C,D是射线OC上一点,连结AD交半圆O于点E,连结BE,CE.
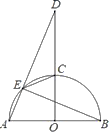 (1)、求证:EC平分∠BED.(2)、当EB=ED时,求证:AE=CE.
(1)、求证:EC平分∠BED.(2)、当EB=ED时,求证:AE=CE. -
23. 小明同学去某批零兼营的文具店,为学校美术小组的30名同学购买铅笔和橡皮.若给全组每人各买2支铅笔和1块橡皮,那么需按零售价购买,共支付30元;若给全组每人各买3支铅笔和2块橡皮,那么可按批发价购买,共支付40.5元.已知1支铅笔的批发价比零售价低0.05元,1块橡皮的批发价比零售价低0.10元.请解决下列问题(均需写出解题过程):(1)、问这家文具店每支铅笔和每块橡皮的批发价各是多少元?(2)、小亮同学用4元钱在这家文具店按零售价买同样的铅笔和橡皮(两样都要买,4元钱恰好用完),有哪几种购买方案?
-
24. 如图,AB是⊙O的直径,弦BC=OB,点D是 上一动点,点E是CD中点,连接BD分别交OC,OE于点F,G.
 (1)、求∠DGE的度数;(2)、若 = ,求 的值;(3)、记△CFB,△DGO的面积分别为S1 , S2 , 若 =k,求 的值.(用含k的式子表示)
(1)、求∠DGE的度数;(2)、若 = ,求 的值;(3)、记△CFB,△DGO的面积分别为S1 , S2 , 若 =k,求 的值.(用含k的式子表示)
