浙江省台州市2019届九年级中考数学模拟试题（3月份）

试卷更新日期：2019-06-17 类型：中考模拟

进入出卷网下载

一、单选题

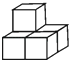
1. 下列说法正确的是（）

A、负数没有倒数 B、正数的倒数比自身小 C、任何有理数都有倒数 D、 $- 1$ 的倒数是 $- 1$

查看试题解析
2. 如图，由5个完全相同的小正方体组合成一个立体图形，它的左视图是（）

A、 B、 C、 D、

查看试题解析
3. 我县人口约为530060人，用科学记数法可表示为（）

A、53006×10人 B、5.3006×10⁵人 C、53×10⁴人 D、0.53×10⁶人

查看试题解析
4. 下列说法正确的个数是（）
①一组数据的众数只有一个②样本的方差越小，波动性越小，说明样本稳定性越好③一组数据的中位数一定是这组数据中的某一数据④数据：1，1，3，1，1，2的众数为4 ⑤一组数据的方差一定是正数.

A、0个 B、1个 C、2个 D、4个

查看试题解析
5. 已知⊙O的半径为10，圆心O到弦AB的距离为5，则弦AB所对的圆周角的度数是（）

A、30° B、60° C、30°或150° D、60°或120°

查看试题解析
6. 下列运算正确的是（）

A、ab•ab＝2ab B、（3a）³＝9a³ C、4 $\sqrt{a}$ ﹣3 $\sqrt{a}$ ＝3（a≥0） D、 $\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}$ （a≥0，b≥0）

查看试题解析
7. 下列说法错误的是（）

A、两组对边分别平行的四边形是平行四边形 B、两组对边分别相等的四边形是平行四边形 C、一组对边平行，另一组对边相等的四边形是平行四边形 D、一组对边平行且相等的四边形是平行四边形

查看试题解析
8. “五一”江北水城文化旅游节期间，几名同学包租一辆面包车前去旅游，面包车的租价为180元，出发时又增加了两名同学，结果每个同学比原来少摊了3元钱车费，设原来参加游览的同学共x人，则所列方程为（）

A、 $\frac{180}{x - 2} - \frac{180}{x} = 3$ B、 $\frac{180}{x + 2} - \frac{180}{x} = 3$ C、 $\frac{180}{x} - \frac{180}{x - 2} = 3$ D、 $\frac{180}{x} - \frac{180}{x + 2} = 3$

查看试题解析
9. 正方形A₁B₁C₁O，A₂B₂C₂C₁ ， A₃B₃C₃C₂ ， …按如图的方式放置.点A₁ ， A₂ ， A₃ ， …和点C₁ ， C₂ ， C₃ ， …分别在直线y=x+1和x轴上，则点B₆的坐标是（）

A、（63，32） B、（64，32） C、（63，31） D、（64，31）

查看试题解析
10. 如图，在等边△ABC中，D是边AC上一点，连接BD，将△BCD绕点B逆时针旋转60°，得到△BAE，连接ED，若BC＝10，BD＝9，则△ADE的周长为（）

A、19 B、20 C、27 D、30

查看试题解析

二、填空题

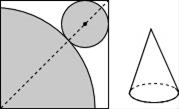
11. 分解因式：3x²﹣6x²y+3xy²= ．

查看试题解析
12. 已知关于x、y的二元一次方程组 ${\begin{matrix} x + y = 5 - m \\ x - 2 y = m + 1 \end{matrix}$ ，则4x²﹣4xy+y²的值为．

查看试题解析
13. 在纸上剪下一个圆和一个扇形纸片，使它们恰好围成一个圆锥（如图所示），如果扇形的圆心角为90°，扇形的半径为4，那么所围成的圆锥的高为.

查看试题解析
14. 袋中装有一个红球和二个黄球，它们除了颜色外都相同，随机从中摸出一球，记录下颜色后放回袋中，充分摇匀后，再随机摸出一球，两次都摸到红球的概率是．

查看试题解析
15. 如图，在△ABC中，AB＝AC，∠A＝36°，BD平分∠ABC交AC于点D，则下列结论中①BC＝BD＝AD；②S_△_ABD：S_△_BCD＝AD：DC；③BC²＝CD•AC；④若AB＝2，则BC＝ $\sqrt{5}$ ﹣1，其中正确的结论的个数是个.

查看试题解析
16. 如图，已知∠MON＝30°，B为OM上一点，BA⊥ON于A，四边形ABCD为正方形，P为射线BM上一动点，连结CP，将CP绕点C顺时针方向旋转90°得CE，连结BE，若AB＝4，则BE的最小值为.

查看试题解析

三、解答题

17. 计算：|﹣1+ $\sqrt{2}$ |﹣ $\frac{1}{2}$ $\sqrt{8}$ ﹣（5﹣π）⁰+4cos45°．

查看试题解析
18. 解不等式组，并将解集在数轴上表示出来．
${\begin{matrix} 2 x - 7 < 3 (x - 1) ① \\ 5 - \frac{1}{2} (x + 4) \geq x ② \end{matrix}$

查看试题解析
19. 一次函数的图象经过点A（2，1）和点B（0，2）.

(1)、求出函数的关系式；

(2)、在平面置角坐标系内画一次函数的图象，回答下列问题：
①y的值随着x的值的增大而，它的图象与x轴的交点坐标是.

②下列点在一次函数图象上的是；

（1， $\frac{3}{2}$ ），（﹣2，3），（6，﹣5）

③当x ，时，y＞0.

查看试题解析
20. 如图，大楼底右侧有一障碍物，在障碍物的旁边有一幢小楼DE，在小楼的顶端D处测得障碍物边缘点C的俯角为30°，测得大楼顶端A的仰角为45°（点B，C，E在同一水平直线上）.已知AB＝80m，DE＝10m，求障碍物B，C两点间的距离.（结果保留根号）

查看试题解析
21. 某校为了解九年级学生体育测试情况，以九年级（1）班学生的体育测试成绩为样本，按A，B，C，D四个等级进行统计，并将统计结果绘制成如下的统计图，请你结合图中所给信息解答下列问题：

（说明：A级：90分～100分；B级：75分～89分；C级：60分～74分；D级：60分以下）

(1)、请把条形统计图补充完整；

(2)、扇形统计图中D级所在的扇形的圆心角度数是多少？

(3)、若该校九年级有600名学生，请用样本估计体育测试中A级学生人数约为多少人？

查看试题解析
22. 已知菱形ABCD的边长为1.∠ADC＝60°，等边△AEF两边分别交边DC、CB于点E、F.

(1)、特殊发现：如图1，若点E、F分别是边DC、CB的中点.求证：菱形ABCD对角线AC、BD交点O即为等边△AEF的外心；

(2)、若点E、F始终分别在边DC、CB上移动.记等边△AEF的外心为点P.
①猜想验证：如图2.猜想△AEF的外心P落在哪一直线上，并加以证明；

②拓展运用：如图3，当△AEF面积最小时，过点P任作一直线分别交边DA于点M，交边DC的延长线于点N，试判断 $\frac{1}{D M} + \frac{1}{D N}$ 是否为定值？若是，请求出该定值；若不是，请说明理由.

查看试题解析
23. 如图，抛物线y＝x²+bx+c与x轴交于点A和B（3，0），与y轴交于点C（0，3）.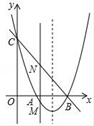

(1)、求抛物线的解析式；

(2)、若点M是抛物线上在x轴下方的动点，过M作MN∥y轴交直线BC于点N，求线段MN的最大值；

(3)、E是抛物线对称轴上一点，F是抛物线上一点，是否存在以A，B，E，F为顶点的四边形是平行四边形？若存在，请直接写出点F的坐标；若不存在，请说明理由.

查看试题解析
24. 如图，AB是⊙O的直径， $\overset{⌢}{A C} = \overset{⌢}{B C}$ ，连结AC，过点C作直线l∥AB，点P是直线l上的一个动点，直线PA与⊙O交于另一点D，连结CD，设直线PB与直线AC交于点E．

(1)、求∠BAC的度数；

(2)、当点D在AB上方，且CD⊥BP时，求证：PC＝AC；

(3)、在点P的运动过程中
①当点A在线段PB的中垂线上或点B在线段PA的中垂线上时，求出所有满足条件的∠ACD的度数；

②设⊙O的半径为6，点E到直线l的距离为3，连结BD，DE，直接写出△BDE的面积．

查看试题解析