浙江省临海市2019届九年级数学中考模拟试卷(3月)
试卷更新日期:2019-06-17 类型:中考模拟
一、单选题
-
1. 绝对值为2的数是( )A、2 B、﹣2 C、±2 D、2. 下列运算正确的是( )A、2a+3a=5a2 B、(a3)3=a9 C、a2•a4=a8 D、a6÷a3=a23. 如图所示的图案中,有2条对称轴的轴对称图形是( )A、
 B、
B、 C、
C、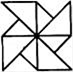 D、
D、 4. 甲、乙两人进行射击比赛,在相同条件下各射击10次,他们的平均成绩一样,而他们的方差分别是S甲2=1.8,S乙2=0.7,则成绩比较稳定的是( )A、甲稳定 B、乙稳定 C、一样稳定 D、无法比较5. 在如图图形中,线段PQ能表示点P到直线L的距离的是( )A、
4. 甲、乙两人进行射击比赛,在相同条件下各射击10次,他们的平均成绩一样,而他们的方差分别是S甲2=1.8,S乙2=0.7,则成绩比较稳定的是( )A、甲稳定 B、乙稳定 C、一样稳定 D、无法比较5. 在如图图形中,线段PQ能表示点P到直线L的距离的是( )A、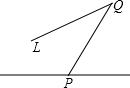 B、
B、 C、
C、 D、
D、 6. 方程 =0的解为( )A、﹣2 B、2 C、5 D、无解7. 已知点A(m+1,﹣2)和点B(3,m﹣1),若直线AB∥x轴,则m的值为( )
6. 方程 =0的解为( )A、﹣2 B、2 C、5 D、无解7. 已知点A(m+1,﹣2)和点B(3,m﹣1),若直线AB∥x轴,则m的值为( )
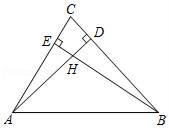
A、2 B、﹣4 C、﹣1 D、38. 如图,△ABC纸片中,AB=BC>AC,点D是AB边的中点,点E在边AC上,将纸片沿DE折叠,使点A落在BC边上的点F处.则下列结论成立的个数有( )①△BDF是等腰直角三角形;②∠DFE=∠CFE;③DE是△ABC的中位线;④BF+CE=DF+DE.
 A、1个 B、2个 C、3个 D、4个9. 如图,AB是⊙O的切线,半径OA=2,OB交⊙O于C,∠B=30°,则劣弧 的长是( )
A、1个 B、2个 C、3个 D、4个9. 如图,AB是⊙O的切线,半径OA=2,OB交⊙O于C,∠B=30°,则劣弧 的长是( )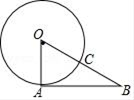 A、 π B、 C、 π D、 π10. 如图是一个圆,一只电子跳蚤在标有数字的五个点上跳跃.若它停在奇数点上时,则一次沿顺时针方向跳两个点;若停在偶数点上时,则下一次沿逆时针方向跳一个点.若这只跳蚤从1这点开始跳,则经过2019次跳后它所停在的点对应的数为( )
A、 π B、 C、 π D、 π10. 如图是一个圆,一只电子跳蚤在标有数字的五个点上跳跃.若它停在奇数点上时,则一次沿顺时针方向跳两个点;若停在偶数点上时,则下一次沿逆时针方向跳一个点.若这只跳蚤从1这点开始跳,则经过2019次跳后它所停在的点对应的数为( )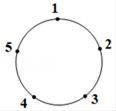 A、1 B、2 C、4 D、5
A、1 B、2 C、4 D、5二、解答题
-
11. 若a、b为实数,且b= +4,则a+b= .12. 求下列各式中的x:(1)、|x|=0;(2)、|x|= ;(3)、﹣|x|=﹣3.7.13. 解方程: .14. 如图,在▱ABCD中,BC=2AB,E,F分别是BC,AD的中点,AE,BF交于点O,连接EF,OC.
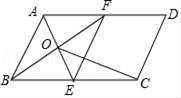 (1)、求证:四边形ABEF是菱形;(2)、若BC=8,∠ABC=60°,求OC的长.15. 某文具店从市场得知如下信息:
(1)、求证:四边形ABEF是菱形;(2)、若BC=8,∠ABC=60°,求OC的长.15. 某文具店从市场得知如下信息:A品牌计算器
B品牌计算器
进价(元/台)
70
100
售价(元/台)
90
140
该文具店计划一次性购进这两种品牌计算器共50台,设该经销商购进A品牌计算器x台,这两种品牌计算器全部销售完后获得利润为y元.
(1)、求y与x之间的函数关系式;(2)、若全部销售完后,获得的利润为1200元,则购进A、B两种品牌计算器的数量各是多少台?(3)、若购进计算器的资金不超过4100元,求该文具店可获得的最大利润是多少元?16. 某校积极参与垃圾分类活动,以班级为单位收集可回收垃圾,下面是七年级各班一周收集的可回收垃圾的质量的频数表和频数直方图(每组含前一个边界值,不含后一个边界值).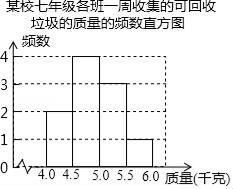
某校七年级各班一周收集的可回收垃圾的质量的频数表
组别(kg)
频数
4.0~4.5
2
4.5~5.0
a
5.0~5.5
3
5.5~6.0
1
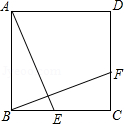
(1)、求a的值(2)、已知收集的可回收垃圾以0.8元/kg被回收,该年级这周收集的可回收垃圾被回收后所得金额能否达到50元?17. 将矩形ABCD绕点A顺时针旋转得到矩形AEFG,点E在BD上; (1)、求证:FD=AB;(2)、连接AF,求证:∠DAF=∠EFA.18. 知识背景
(1)、求证:FD=AB;(2)、连接AF,求证:∠DAF=∠EFA.18. 知识背景当a>0且x>0时,因为( ﹣ )2≥0,所以x﹣2 + ≥0,从而x+ (当x= 时取等号).
设函数y=x+ (a>0,x>0),由上述结论可知:当x= 时,该函数有最小值为2 .
应用举例
已知函数为y1=x(x>0)与函数y2= (x>0),则当x= =2时,y1+y2=x+ 有最小值为2 =4.
解决问题
(1)、已知函数为y1=x+3(x>﹣3)与函数y2=(x+3)2+9(x>﹣3),当x取何值时, 有最小值?最小值是多少?(2)、已知某设备租赁使用成本包含以下三部分:一是设备的安装调试费用,共490元;二是设备的租赁使用费用,每天200元;三是设备的折旧费用,它与使用天数的平方成正比,比例系数为0.001.若设该设备的租赁使用天数为x天,则当x取何值时,该设备平均每天的租货使用成本最低?最低是多少元?19. 阅读理解:如果两个正数a,b,即a>0,b>0,有下面的不等式: ,当且仅当a=b时取到等号我们把 叫做正数a,b的算术平均数,把 叫做正数a,b的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数.它在数学中有广泛的应用,是解决最值问题的有力工具.初步探究:
(1)、已知x>0,求函数y=x+ 的最小值.(2)、学校准备以围墙一面为斜边,用栅栏围成一个面积为100m2的直角三角形,作为英语角,直角三角形的两直角边各为多少时,所用栅栏最短?(3)、如图,在直角坐标系中,直线AB经点P(3,4),与坐标轴正半轴相交于A,B两点,当△AOB的面积最小时,求△AOB的内切圆的半径.
三、填空题