浙江省杭州市萧山区临浦片2019届中考适应性考试数学试卷

试卷更新日期：2019-06-17 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列计算正确的是（）

A、 $\sqrt{- 16}$ =﹣4 B、 $\sqrt{16}$ =±4 C、 $\sqrt{{(- 4)}^{2}}$ =﹣4 D、 $\sqrt[3]{{(- 4)}^{3}}$ =﹣4

查看试题解析
2. 中国倡导的“一带一路”建设将促进我国与世界各国的互利合作，根据规划，“一带一路”地区覆盖总人口约为440000万人，将440000用科学记数法表示为（）

A、4.4×10⁶ B、4.4×10⁵ C、44×10⁴ D、0.44×10⁵

查看试题解析
3. 哥哥身高 $1.68$ 米，在地面上的影子长是 $2.1$ 米，同一时间测得弟弟的影子长 $1.8$ 米，则弟弟身高是（）

A、1.44米 B、1.52米 C、1.96米 D、2.25米

查看试题解析
4. 如图，某厂2004年各季度产值统计图（单位：万元），则下列说法正确的是（）

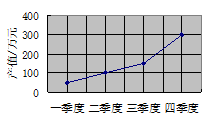A、四个季度中，每个季度生产总值有增有减 B、四个季度中，前三个季度生产总值增长较快 C、四个季度中，各季度的生产总值变化一样 D、第四季度生产总值增长最快

查看试题解析
5. 下列运算中，错误的是（）

A、 $\frac{x - y}{x + y} = - \frac{y - x}{y + x}$ B、 $\frac{- a - b}{a + b} = - 1$ C、 $\sqrt{a^{2}} = a$ D、 $\sqrt{{(1 - \sqrt{2})}^{2}} = \sqrt{2} - 1$

查看试题解析
6. 《九章算术》是中国古代第一部数学专著，它对我国古代后世的数学家产生了深远的影响，该书中记载了一个问题，大意是：有几个人一起去买一件物品，每人出8元，多3元；每人出7元，少4元，问有多少人？该物品价几何？设有x人，物品价值y元，则所列方程组正确的是（）

A、 ${\begin{matrix} 8 y + 3 = x \\ 7 y - 4 = x \end{matrix}$ B、 ${\begin{matrix} 8 x + 3 = y \\ 7 x - 4 = y \end{matrix}$ C、 ${\begin{matrix} 8 x - 3 = y \\ 7 x + 4 = y \end{matrix}$ D、 ${\begin{matrix} 8 y - 3 = x \\ 7 y + 4 = x \end{matrix}$

查看试题解析
7. 下列不等式变形中，错误的是（）

A、若a≥b，则a+c≥b+c B、若a+c≥b+c，则a≥b C、若a≥b，则ac²≥bc² D、若ac²≥bc² ，则a≥b

查看试题解析
8. 小带和小路两个人开车从A城出发匀速行驶至B城.在整个行驶过程中，小带和小路两人的车离开A城的距离y（千米）与行驶的时间t（小时）之间的函数关系如图所示.有下列结论；①A.B两城相距300千米；②小路的车比小带的车晚出发1小时，却早到1小时；③小路的车出发后2.5小时追上小带的车；④当小带和小路的车相距50千米时，t＝ $\frac{5}{4}$ 或t＝ $\frac{15}{4}$ .其中正确的结论有（）

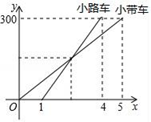A、①②③④ B、①②④ C、①② D、②③④

查看试题解析
9. 如图，直径AB，CD相互垂直，P为弧BC上任意一点，连PC，PA，PD，PB，下列结论：①∠APC＝∠DPE；②∠AED＝∠DFA；③ $\frac{C P + D P}{B P + A P} = \frac{A P}{D P}$ ；其中正确的是（）

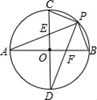A、①③ B、只有① C、只有② D、①②③

查看试题解析
10. 如图，在由边长为1的小正方形组成的网格中，点A，B，C，D都在这些小正方形的格点上，AB，CD相交于点E，则sin∠AEC的值为（）

A、 $\frac{2 \sqrt{5}}{5}$ B、 $\frac{3 \sqrt{5}}{10}$ C、 $\frac{1}{2}$ D、 $\frac{\sqrt{10}}{4}$

查看试题解析

二、填空题

11. 若a^m=5，aⁿ=6，则a^m+n=。

查看试题解析
12. 分解因式：3x²﹣6x²y+3xy²= ．

查看试题解析
13. 如图，直线l与x轴、y轴分别交于点A、B，且OB＝4，∠ABO＝30°，一个半径为1的⊙C，圆心C从点(0，1)开始沿y轴向下运动，当⊙C与直线l相切时，⊙C运动的距离是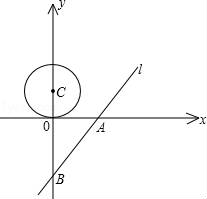

查看试题解析
14. 袋中装有一个红球和二个黄球，它们除了颜色外都相同，随机从中摸出一球，记录下颜色后放回袋中，充分摇匀后，再随机摸出一球，两次都摸到红球的概率是．

查看试题解析
15. 平行四边形两条对角线的长分别为8cm，6cm，则它的一边长a的取值范围是.

查看试题解析
16. 数学课上，老师提出如下问题：△ABC是⊙O的内接三角形，OD⊥BC于点D.请借助直尺，画出△ABC中∠BAC的平分线.
晓龙同学的画图步骤如下：

①延长OD交 $\overset{⌢}{B C}$ 于点M；

②连接AM交BC于点N.

所以线段AN为所求△ABC中∠BAC的平分线.

请回答：晓龙同学画图的依据是.

查看试题解析

三、解答题

17. 浙江实施“五水共治“以来，越来越重视节约用水，某地对居民用水按阶梯水价方式进行收费，人均月生活用水收费标准如图所示，图中x表示人均月生活用水的吨数，y表示收取的人均月生活用水费（元），请根据图象信息，回答下列问题.

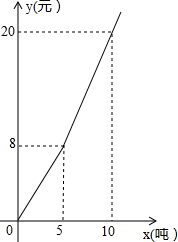(1)、请写出y与x的函数关系式；

(2)、若某个家庭有5人，响应节水号召，计划控制1月份的生活用水费不超过76元，则该家庭这个月最多可以用多少吨水？

查看试题解析
18. 我市某中学为了了解孩子们对《中国诗词大会》、《挑战不可能》、《最强大脑》、《超级演说家》、《地理中国》五种电视节目的喜爱程度，随机在七、八、九年级抽取了部分学生进行调查（每人只能选择一种喜爱的电视节目），并将获得的数据进行整理，绘制出以下两幅不完整的统计图，请根据两幅统计图中的信息回答下列问题：

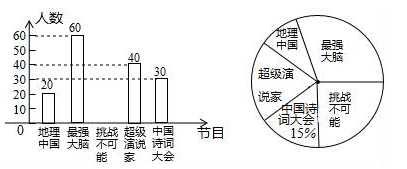(1)、本次调查中共抽取了名学生.

(2)、补全条形统计图.

(3)、在扇形统计图中，喜爱《地理中国》节目的人数所在的扇形的圆心角是度.

查看试题解析
19. 如图，已知等腰三角形ADC，AD＝AC，B是线段DC上的一点，连结AB，且有AB＝DB.

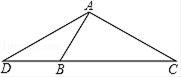(1)、求证：△ADB∽△CDA；

(2)、若DB＝2，BC＝3，求AD的值.

查看试题解析
20. 如图，在平面直角坐标中，点O是坐标原点，一次函数y₁＝kx+b与反比例函数y₂＝ $\frac{3}{x}$ （x＞0）的图象交于A（1，m）、B（n，1）两点.

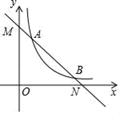(1)、求直线AB的解析式及△OAB面积；

(2)、根据图象写出当y₁＜y₂时，x的取值范围；

(3)、若点P在x轴上，求PA+PB的最小值.

查看试题解析
21. 如图，已知一张长方形纸片，AB＝CD＝a，AD＝BC＝b（a＜b＜2a）.
将这张纸片沿着过点A的折痕翻折，使点B落在AD边上的点F，折痕交BC于点E，将折叠后的纸片再次沿着另一条过点A的折痕翻折，点E恰好与点D重合，此时折痕交DC于点G.

(1)、在图中确定点F、点E和点G的位置；

(2)、连接AE，则∠EAB＝°；

(3)、用含有a、b的代数式表示线段DG的长.

查看试题解析
22. 用描点法在同一直角坐标系中画出y₁＝|x|和y₂＝x+1的图象，并根据图象回答：

(1)、当x在什么范围时，y₁＜y₂？

(2)、当x在什么范围时，y₁＞y₂？

查看试题解析