云南省曲靖市2019届数学中考一模试卷
试卷更新日期:2019-06-17 类型:中考模拟
一、单选题
-
1. 下列图形中既是轴对称图形,又是中心对称图形的是A、
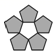 B、
B、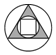 C、
C、 D、
D、 2. 下列是一元二次方程的是A、 B、 C、 D、3. 半径为r的圆的内接正六边形边长为A、 B、 C、r D、2r4. 如图,这是一幅2018年俄罗斯世界杯的长方形宣传画,长为4m,宽为 为测量画上世界杯图案的面积,现将宣传画平铺在地上,向长方形宣传画内随机投掷骰子 假设骰子落在长方形内的每一点都是等可能的 ,经过大量重复投掷试验,发现骰子落在世界杯图案中的频率稳定在常数 左右 由此可估计宣传画上世界杯图案的面积为
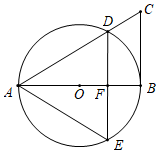
2. 下列是一元二次方程的是A、 B、 C、 D、3. 半径为r的圆的内接正六边形边长为A、 B、 C、r D、2r4. 如图,这是一幅2018年俄罗斯世界杯的长方形宣传画,长为4m,宽为 为测量画上世界杯图案的面积,现将宣传画平铺在地上,向长方形宣传画内随机投掷骰子 假设骰子落在长方形内的每一点都是等可能的 ,经过大量重复投掷试验,发现骰子落在世界杯图案中的频率稳定在常数 左右 由此可估计宣传画上世界杯图案的面积为 A、 B、 C、 D、5. 在平面直角坐标系中,点(1,﹣2)关于原点对称的点的坐标是( )A、(1,2) B、(﹣1,2) C、(2,﹣1) D、(2,1)6. 下列事件中必然发生的事件是A、一个图形平移后所得的图形与原来的图形不一定全等 B、不等式的两边同时乘以一个数,结果仍是不等式 C、过圆外一点引圆的两条切线,这两条切线的长度不一定相等 D、200件产品中有8件次品,从中任意抽取9件,至少有一件是正品7. 如图,四边形ABCD是 的内接四边形,若 ,则 的度数是
A、 B、 C、 D、5. 在平面直角坐标系中,点(1,﹣2)关于原点对称的点的坐标是( )A、(1,2) B、(﹣1,2) C、(2,﹣1) D、(2,1)6. 下列事件中必然发生的事件是A、一个图形平移后所得的图形与原来的图形不一定全等 B、不等式的两边同时乘以一个数,结果仍是不等式 C、过圆外一点引圆的两条切线,这两条切线的长度不一定相等 D、200件产品中有8件次品,从中任意抽取9件,至少有一件是正品7. 如图,四边形ABCD是 的内接四边形,若 ,则 的度数是 A、 B、 C、 D、8. 为把我市创建成全国文明城市,某社区积极响应市政府号召,准备在一块正方形的空地上划出部分区域栽种鲜花,如图中的阴影“
A、 B、 C、 D、8. 为把我市创建成全国文明城市,某社区积极响应市政府号召,准备在一块正方形的空地上划出部分区域栽种鲜花,如图中的阴影“ ”带,鲜花带一边宽1m,另一边宽2m,剩余空地的面积为 ,求原正方形空地的边长xm,可列方程为
”带,鲜花带一边宽1m,另一边宽2m,剩余空地的面积为 ,求原正方形空地的边长xm,可列方程为 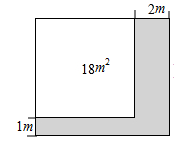 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
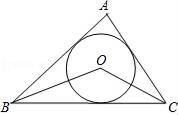
9. 若式子 有意义,则x的取值范围是.10. 如图,已知点O是△ABC的内切圆的圆心,若∠BOC=124°,则∠A=.
 11. 若 ,则多项式 .12. 圆锥的母线长是6cm,侧面积是30πcm2 , 该圆锥底面圆的半径长等于cm.13. 若 是关于自变量x的二次函数,则 .14. 如图所示,在平面直角坐标系中, , , 是等腰直角三角形且 ,把 绕点B顺时针旋转 ,得到 ,把 绕点C顺时针旋转 ,得到 ,依此类推,得到的等腰直角三角形的直角顶点 的坐标为.
11. 若 ,则多项式 .12. 圆锥的母线长是6cm,侧面积是30πcm2 , 该圆锥底面圆的半径长等于cm.13. 若 是关于自变量x的二次函数,则 .14. 如图所示,在平面直角坐标系中, , , 是等腰直角三角形且 ,把 绕点B顺时针旋转 ,得到 ,把 绕点C顺时针旋转 ,得到 ,依此类推,得到的等腰直角三角形的直角顶点 的坐标为.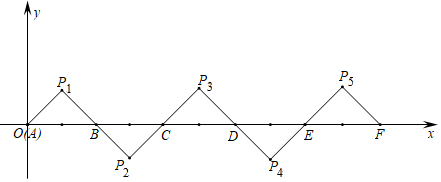
三、解答题
-
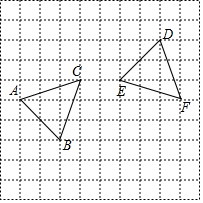
15. 先化简,再求值: ,其中 .16. 计算:17. 如图,在边长均为1的正方形网格纸上有 和 ,顶点A、B,C,D、E、F均在格点上,如果 是由 绕着某点O旋转得到的,点 的对应点是点D,点C的对应点是点 请按要求完成以下操作或运算:
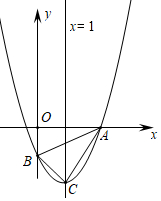
 (1)、在图上找到点O的位置 不写作法,但要标出字母 ,并写出点O的坐标;(2)、求点B绕着点O顺时针旋转到点E所经过的路径长.18. 解方程:(1)、x2-4x+3=0(用配方法求解)(2)、(2x-3)2-2x+3=019. 已知 是关于x的抛物线解析式.(1)、求证:抛物线与x轴一定有两个交点;(2)、点 、 、 是抛物线上的三个点,当抛物线经过原点时,判断 、 、 的大小关系.20. 一不透明的布袋里,装有红、黄、蓝三种颜色的小球(除颜色外其余都相同),其中有红球2个,蓝球1个,黄球若干个,现从中任意摸出一个球是红球的概率为 .(1)、求口袋中黄球的个数;(2)、甲同学先随机摸出一个小球(不放回),再随机摸出一个小球,请用“树状图法”或“列表法”,求两次摸出都是红球的概率;21. 某网店经营一种新文具,进价为20元,销售一段时间后统计发现:当销售单价是25元时,平均每天的销售量为250件,销售单价每上涨1元,平均每天的销售量就减少10件.(1)、求销售单价 元 为多少时,该文具每天的销售利润 元 最大?并求出W;(2)、为回馈广大顾客同时提高该文具知名度,该网店决定在11月11日 双十一 开展降价促销活动 若当天按 的单价降价 销售并多售出 件文具,求销售款额为5250时m的值.
(1)、在图上找到点O的位置 不写作法,但要标出字母 ,并写出点O的坐标;(2)、求点B绕着点O顺时针旋转到点E所经过的路径长.18. 解方程:(1)、x2-4x+3=0(用配方法求解)(2)、(2x-3)2-2x+3=019. 已知 是关于x的抛物线解析式.(1)、求证:抛物线与x轴一定有两个交点;(2)、点 、 、 是抛物线上的三个点,当抛物线经过原点时,判断 、 、 的大小关系.20. 一不透明的布袋里,装有红、黄、蓝三种颜色的小球(除颜色外其余都相同),其中有红球2个,蓝球1个,黄球若干个,现从中任意摸出一个球是红球的概率为 .(1)、求口袋中黄球的个数;(2)、甲同学先随机摸出一个小球(不放回),再随机摸出一个小球,请用“树状图法”或“列表法”,求两次摸出都是红球的概率;21. 某网店经营一种新文具,进价为20元,销售一段时间后统计发现:当销售单价是25元时,平均每天的销售量为250件,销售单价每上涨1元,平均每天的销售量就减少10件.(1)、求销售单价 元 为多少时,该文具每天的销售利润 元 最大?并求出W;(2)、为回馈广大顾客同时提高该文具知名度,该网店决定在11月11日 双十一 开展降价促销活动 若当天按 的单价降价 销售并多售出 件文具,求销售款额为5250时m的值.