吉林省长春市南关区2019届数学中考一模试卷
试卷更新日期:2019-06-17 类型:中考模拟
一、单选题
-
1. 据统计, 年春运全国铁路累计发送旅客约 人次, 这个数用科学记数法表示为( )A、 B、 C、 D、2. 不等式 的解集在数轴上表示正确的是( )A、
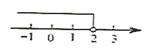 B、
B、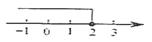 C、
C、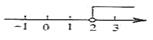 D、
D、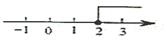 3. 如图是由 个相同的小正方体组成的立体图形,这个立体图形的俯视图是( )
3. 如图是由 个相同的小正方体组成的立体图形,这个立体图形的俯视图是( )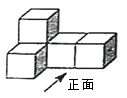 A、
A、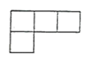 B、
B、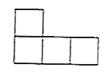 C、
C、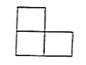 D、
D、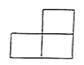 4. 如图,在 中, 平分 交边 于点 ,若 , ,则 的大小为( )
4. 如图,在 中, 平分 交边 于点 ,若 , ,则 的大小为( )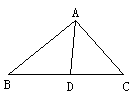 A、 B、 C、 D、5. 如图,某超市自动扶梯的倾斜角 为 ,扶梯长 为 米,则扶梯高 的长为( )
A、 B、 C、 D、5. 如图,某超市自动扶梯的倾斜角 为 ,扶梯长 为 米,则扶梯高 的长为( )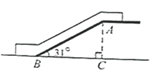 A、 米 B、 米 C、 米 D、 米6. 已知 ,用尺规作图的方法在 上确定一点 ,使 ,下列作图正确的是( )A、
A、 米 B、 米 C、 米 D、 米6. 已知 ,用尺规作图的方法在 上确定一点 ,使 ,下列作图正确的是( )A、 B、
B、 C、
C、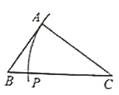 D、
D、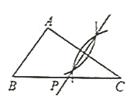 7. 如图,在平面直角坐标系中, 的顶点 、 在函数 的图象上,轴.若 且BC∥x轴,点 、 的横坐标分别为 、 , 的面积为 ,则 的值为( )
7. 如图,在平面直角坐标系中, 的顶点 、 在函数 的图象上,轴.若 且BC∥x轴,点 、 的横坐标分别为 、 , 的面积为 ,则 的值为( )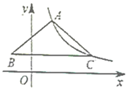 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
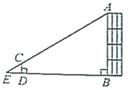
8. 比较大小: 2.(填“>”、“=”、“<”)9. 计算: .10. 若关于x的一元二次方程x2+2x﹣m=0有两个相等的实数根,则m的值为 .11. 利用标杆 测量建筑物的高度的示意图如图所示,若标杆 的高为 米,测得 米, 米,则建筑物的高 为米.
 12. 如图,在 中, ,点 为 的中点,将 绕点 按顺时针方向旋转,当 经过点 时得到 ,若 , ,则 的长为.
12. 如图,在 中, ,点 为 的中点,将 绕点 按顺时针方向旋转,当 经过点 时得到 ,若 , ,则 的长为.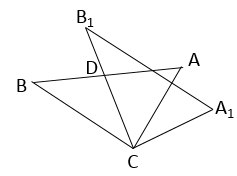
三、解答题
-
13. 先化简,再求值: ,其中 .14. 一个不透明的口袋中有三个小球,上面分别标有数字 , , ,除所标数字不同外,其它完全相同,从中随机摸出一个小球,记下数字后放回并搅匀,再随机摸出一个小球.用画树状图(或列表)的方法,求两次摸出的小球所标数字之和大于 的概率.15. 图①、图②均是边长为 的小正方形组成的 网格,每个小正方形的顶点称为格点,点 、 、 均在格点上,按下列要求画出顶点均在格点上的四边形.
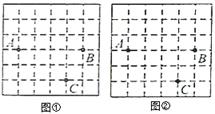 (1)、在图①中确定顶点 ,并画出以 、 、 、 为顶点的四边形,使其为轴对称图形.(2)、在图②中确定顶点 ,并画出以 、 、 、 为顶点的四边形,使其为中心对称图形.(图①、图②中各画出一个符合条件的四边形即可)16. 如图, 是⊙ 的直径, 切⊙ 于点 , 交⊙ 于点 的半径为 , .
(1)、在图①中确定顶点 ,并画出以 、 、 、 为顶点的四边形,使其为轴对称图形.(2)、在图②中确定顶点 ,并画出以 、 、 、 为顶点的四边形,使其为中心对称图形.(图①、图②中各画出一个符合条件的四边形即可)16. 如图, 是⊙ 的直径, 切⊙ 于点 , 交⊙ 于点 的半径为 , . (1)、求 的度数;(2)、求 的长.(结果保留 )17. 某地区由于龙卷风出现毁坏性灾害,一自愿者协会紧急筹集资金,计划购买甲、乙两种救灾物品送往该地区.已知甲种物品每件的价格比乙种物品每件的价格高 元,用 元购买甲种物品的件数与用 元购买乙种物品的件数相同.(1)、求甲、乙两种救灾物品每件的价格.(2)、经调查,该地区所需乙种物品的件数是甲种物品件数的 倍,自愿者协会按此比例购买 件物品,需筹集资金多少元?18. 某校为提高学生的汉字书写能力,开展了“汉字听写”大赛.七、八年级各有 人参加比赛,为了解这两个年级参加比赛学生的成绩情况,从中各随机抽取 名学生的成绩,数据如下:
(1)、求 的度数;(2)、求 的长.(结果保留 )17. 某地区由于龙卷风出现毁坏性灾害,一自愿者协会紧急筹集资金,计划购买甲、乙两种救灾物品送往该地区.已知甲种物品每件的价格比乙种物品每件的价格高 元,用 元购买甲种物品的件数与用 元购买乙种物品的件数相同.(1)、求甲、乙两种救灾物品每件的价格.(2)、经调查,该地区所需乙种物品的件数是甲种物品件数的 倍,自愿者协会按此比例购买 件物品,需筹集资金多少元?18. 某校为提高学生的汉字书写能力,开展了“汉字听写”大赛.七、八年级各有 人参加比赛,为了解这两个年级参加比赛学生的成绩情况,从中各随机抽取 名学生的成绩,数据如下:七年级
八年级
(1)、整理数据 按如下分段整理本数据并补全表格:人数
成绩
年级
七年级
八年级
分析数据 补全下列表格中的统计量:
统计量
年级
平均数
中位数
众数
方差
七年级
八年级
(2)、得出结论
估计该校八年级参加这次“汉字听写”大赛成绩低于 分的人数.(3)、你认为哪个年级学生“汉字听写”大赛的成绩比较好?并说明理由.(写一条即可)19. 甲、乙两车间同时开始加工一批零件,加工一段时间后,甲车间的设备出现故障停产维修设备,乙车间继续加工,甲车间维修好设备后提高了工作效率,每小时比出现故障前多加工 个零件,从开始加工到加工完这批零件乙车间的工作效率不变且工作 小时.甲、乙两车间加工这批零件的总数量 (件)与加工时间 (时)之间的函数图象如图所示.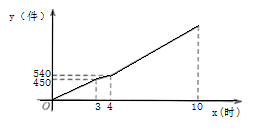 (1)、甲车间每小时加工零件多少个;(2)、求甲车间维修完设备后, 与 之间的函数关系;(3)、求加工这批零件总数量的 时所用的时间.20. 在 中, , .过点 作射线 ,点 M,、N分别在边 、 上(点 、 不与所在线段端点重合),且 ,连结 并延长交 于点 ,连结 并延长交 的垂直平分线于点 ,连结 .
(1)、甲车间每小时加工零件多少个;(2)、求甲车间维修完设备后, 与 之间的函数关系;(3)、求加工这批零件总数量的 时所用的时间.20. 在 中, , .过点 作射线 ,点 M,、N分别在边 、 上(点 、 不与所在线段端点重合),且 ,连结 并延长交 于点 ,连结 并延长交 的垂直平分线于点 ,连结 . (1)、【猜想】如图①,当 时,可证 .从而得出 ,进而得出 的大小为多少度.(2)、【探究】如图②,若 .
(1)、【猜想】如图①,当 时,可证 .从而得出 ,进而得出 的大小为多少度.(2)、【探究】如图②,若 .Ⅰ.求证: .
Ⅱ. 的大小为多少度(用含 的代数式表示)
(3)、【应用】如图③,当 时,连结 .若 , ,则 的面积为多少.