吉林省长春市朝阳区2019届数学中考一模试卷

试卷更新日期：2019-06-17 类型：中考模拟

进入出卷网下载

一、单选题

1. 2019的相反数是（）

A、 $- \frac{1}{2019}$ B、 $\frac{1}{2019}$ C、2019 D、-2019

查看试题解析
2. 据统计，在深圳市举行的国际汽车博览会成交额约为6058000000元，6058000000这个数用科学记数法表示为（）

A、60.58×10¹⁰ B、6.058×10¹⁰ C、6.058×10⁹ D、6.058×10⁸

查看试题解析
3. 把多项式 $a^{3} - a$ 分解因式，结果正确的是（）

A、 $a (a^{2} -1)$ B、 $a {(a-1)}^{2}$ C、 $a {(a+1)}^{2}$ D、 $a (a+1) (a-1)$

查看试题解析
4. 下列几何体中，主视图和俯视图都为矩形的是（　　）

A、 B、 C、 D、

查看试题解析
5. 不等式组 ${\begin{matrix} 3 x - 1 > 2 \\ 4 - 2 x \geq 0 \end{matrix}$ 的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
6. 关于x的一元二次方程 $2 x^{2} - 4 x + 1 = 0$ 的根的情况是（）

A、没有实数根. B、有一个实数根. C、有两个相等的. D、有两个不相等的实数根.

查看试题解析
7. 如图，直线 $y=x+b$ 与直线 $y = kx + 4$ 交于点 $P (\frac{2}{3} ， \frac{8}{3})$ ，关于x的不等式 $x + b > kx + 4$ 的解集是（）

A、 $x > \frac{2}{3}$ B、 $x \geq \frac{2}{3}$ C、 $x < \frac{2}{3}$ D、 $x \leq \frac{2}{3}$

查看试题解析
8. 如图，在平面直角坐标系中，过反比例函数y= $\frac{k}{x}$ （k＜0，＜0）的图象上一点A作AB⊥x轴于B，连结AO，过点B作BC∥AO交y轴于点C.若点A的纵坐标为4，且tan∠BCO= $\frac{3}{2}$ ，则k的值为（）

A、 $- 6$ B、 $- 12$ C、 $- 24$ D、24

查看试题解析

二、填空题

9. 写出一个比5大且比6小的无理数.

查看试题解析
10. 《九章算术》是中国传统数学最重要的著作，方程术是《九章算术》最高的数学成就．《九章算术》中记载：今有牛五、羊二，直金十两；牛二、羊五，直金八两．问：牛、羊各直金几何？译文：假设有5头牛、2只羊，值金10两；2头牛、5只羊，值金8两．问每头牛、每只羊各值金多少？若设每头牛值金x两，每只羊值金y两，可列方程组为．

查看试题解析
11. 如图，AB∥CD.若∠ACD=82°，∠CED=29°，则∠ABD的大小为度.

查看试题解析
12. 如图，海面上B、C两岛分别位于A岛的正东和正北方向，A岛与C岛之间的距离约为36海里，B岛在C岛的南偏东43°，A、B两岛之间的距离约为海里（结果精确到0.1海里）（参考数据：sin43°=0.68，cos43°=0.73，tan43°=0.93）

查看试题解析
13. 如图，在平面直角坐标系中，抛物线y= $\frac{1}{4} {(x - 3)}^{2}$ -1的顶点为A，直线l过点P（0，m）且平行于x轴，与抛物线交于点B和点C.若AB=AC，∠BAC=90°，则m=.

查看试题解析
14. 在数学课上，老师提出如下问题：
已知：直线l和直线外的一点P.

求作：过点P作直线 $PQ ⊥ l$ 于点Q.

已知：直线l和直线外的一点P.

求作：过点P作直线 $PQ ⊥ l$ 于点Q.

小华的作法如下：

如图，第一步：以点P为圆心，适当长度为半径作弧，交直线于A，B两点；

第二步：连接PA、PB，作 $∠ APB$ 的平分线，交直线l于点Q.直线PQ即为所求作.

如图，第一步：以点P为圆心，适当长度为半径作弧，交直线于A，B两点；

第二步：连接PA、PB，作 $∠ APB$ 的平分线，交直线l于点Q.直线PQ即为所求作.

老师说：“小华的作法正确”.

请回答：小华第二步作图的依据是.

查看试题解析

三、解答题

15. 先化简，再求值：（x+1）²+x（x-2），其中x=- $\sqrt{2}$ .

查看试题解析
16. 一个不透明的口袋中装有三个小球，上面分别标有数字3、4、5，这些小球除数字不同外其余均相同.

(1)、从口袋中随机摸出一个小球，小球上的数字是偶数的概率是.

(2)、从口袋中随机摸出一个小球，记下数字后放回，再随机摸出一个小球，记下数字，请用画树状图（或列表）的方法，求两次摸出的小球上的数字都是奇数的概率.

查看试题解析
17. 如图，在⊙O中，点C为OB的中点，点D为弦AB的中点，连结CD并延长，交过点A的切线于点E.求证：AE⊥CE.

查看试题解析
18. 甲、乙两名同学做中国结.已知甲每小时比乙少做6个中国结，甲做30个中国结所用的时间与乙做45个中国结所用的时间相同，求甲每小时做中国结的个数.

查看试题解析
19. 如图，E是平行四边形ABCD的边BA延长线上一点，AE=AB，连结AC、DE、CE.

(1)、求证：四边形ACDE为平行四边形.

(2)、若AB=AC，AD=4，CE=6，求四边形ACDE的面积.

查看试题解析

20. 张老师计划通过步行锻炼身体，她用运动手环连续记录了6天的运动情况，并用统计表和统计图记录数据：

日期	4月1日	4月2日	4月3日	4月4日	4月5日	4月6日
步行数(步)	10672	4927	5543	6648
步行距离(公里)	6.8	3.1	3.5	4.6
卡路里消耗(千卡)	157	73	82	107
燃烧脂肪(克)	20	10	12	16

(1)、.请你将手环记录的4月5日和4月6日的数据(如图①)填入表格.

(2)、.请你将条形统计图(如图②)补充完整.

(3)、.张老师这6天平均每天约步行公里，张老师分析发现每天步行距离和消耗的卡路里近似成正比例关系，她打算每天消耗的卡路里至少达到100千卡，那么每天步行距离大约至少为公里(精确到0.1公里).

查看试题解析

21. 某校初三年级进行女子800米测试，甲、乙两名同学同时起跑，甲同学先以a米/秒的速度匀速跑，一段时间后提高速度，以 $\frac{5}{3} a$ 米/秒的速度匀速跑，b秒到达终点，乙同学在第60秒和第140秒时分别减慢了速度，设甲、乙两名同学所的路程为s（米），乙同学所用的时间为t（秒），s与t之间的函数图象如图所示.

(1)、乙同学起跑的速度为米/秒；

(2)、求a、b的值；

(3)、当乙同学领先甲同学60米时，直接写出t的值是.

查看试题解析
22. （感知）如图①，点C是AB中点，CD⊥AB，P是CD上任意一点，由三角形全等的判定方法“SAS”易证△PAC≌△PBC，得到线段垂直平分线的一条性质“线段垂直平分线上的点到线段两端的距离相等”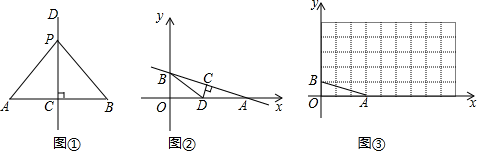

（探究）如图②，在平面直角坐标系中，直线y=- $\frac{1}{3}$ x+1分别交x轴、y轴于点A和点B，点C是AB中点，CD⊥AB交OA于点D，连结BD，求BD的长

（应用）如图③

(1)、将线段AB绕点A顺时针旋转90°得到线段AB′，请在图③网格中画出线段AB；

(2)、若存在一点P，使得PA=PB′，且∠APB′≠90°，当点P的横、纵坐标均为整数时，则AP长度的最小值为.

查看试题解析
23. 如图，在 $Rt △ ABC$ 中， $∠ ABC = 90 °$ ， $AB = 4$ ， $BC = 2$ .点P从点A出发，以每秒 $\sqrt{5}$ 个单位长度的速度向终点C运动.点Q从点B出发，以每秒2个单位长度的速度向终点A运动.连结PQ，将线段PQ绕点Q顺时针旋转 $90 °$ 得到线段QE，以PQ、QE为边作正方形PQEF.设点P运动的时间为t秒 $(t > 0)$ .

(1)、点P到边AB的距离为(用含t的代数式表示).

(2)、当 $PQ / / BC$ 时，求t的值.

(3)、连结BE.设 $△ BEQ$ 的面积为S，求S与t之间的函数关系式.

查看试题解析
24. 在平面直角坐标系中，已知抛物线y=x²-2mx-3m

(1)、当m=1时，
①抛物线的对称轴为直线，
②抛物线上一点P到x轴的距离为4，求点P的坐标
③当n≤x≤ $\frac{1}{2}$ 时，函数值y的取值范围是- $\frac{15}{4}$ ≤y≤2-n，求n的值

(2)、设抛物线y=x²-2mx-3m在2m-1≤x≤2m+1上最低点的纵坐标为y₀ ，直接写出y₀与m之间的函数关系式及m的取值范围.

查看试题解析