吉林省长春市2019届数学中考一模试卷
试卷更新日期:2019-06-17 类型:中考模拟
一、单选题
-
1. ﹣ 的绝对值是( )A、﹣2019 B、2019 C、﹣ D、2. 据统计,截止2019年2月,长春市实际居住人口约4210000人,4210000这个数用科学记数法表示为( )A、 B、 C、 D、3. 如图是一个正六棱柱的茶叶盒,其俯视图为( )
 A、
A、 B、
B、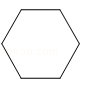 C、
C、 D、
D、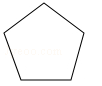 4. 不等式 的解集在数轴上表示正确的是( )A、
4. 不等式 的解集在数轴上表示正确的是( )A、 B、
B、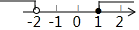 C、
C、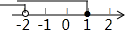 D、
D、 5. 已知如图,△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )
5. 已知如图,△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( ) A、 B、 C、 D、6. 如图所示,某超市在一楼至二楼之间安装有电梯,天花板与地面平行.张强扛着箱子(人与箱子的总高度约为2.2m)乘电梯刚好安全通过,请你根据图中数据回答,两层楼之间的高约为( )
A、 B、 C、 D、6. 如图所示,某超市在一楼至二楼之间安装有电梯,天花板与地面平行.张强扛着箱子(人与箱子的总高度约为2.2m)乘电梯刚好安全通过,请你根据图中数据回答,两层楼之间的高约为( )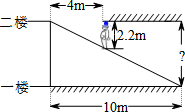 A、 B、 C、11m D、7. 如图,某地修建高速公路,要从B地向C地修一座隧道(B,C在同一水平面上),为了测量B,C两地之间的距离,某工程师乘坐热气球从C地出发,垂直上升200米到达A处,在A处观察B地的俯角为α,则B,C两地之间的距离为( )
A、 B、 C、11m D、7. 如图,某地修建高速公路,要从B地向C地修一座隧道(B,C在同一水平面上),为了测量B,C两地之间的距离,某工程师乘坐热气球从C地出发,垂直上升200米到达A处,在A处观察B地的俯角为α,则B,C两地之间的距离为( )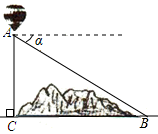 A、 米 B、 米 C、 米 D、 米8. 如图,在平面直角坐标系中,点A,B的坐标分贝为(0,3)、(1,0),将线段AB绕点B顺时针旋转90°,得到线段BC,若点C落在函数y= (x>0)的图象上,则k的值为( )
A、 米 B、 米 C、 米 D、 米8. 如图,在平面直角坐标系中,点A,B的坐标分贝为(0,3)、(1,0),将线段AB绕点B顺时针旋转90°,得到线段BC,若点C落在函数y= (x>0)的图象上,则k的值为( ) A、3 B、4 C、6 D、8
A、3 B、4 C、6 D、8二、填空题
-
9. 比较大小: 3(填写“<”或“>”).10. (a2)3= .
11. 如图,直线L:y=- x-3与直线y=a(a为常数)的交点在第三象限,则a的值可以为.(写出一个即可)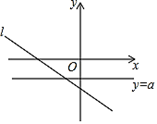 12. 如图,四边形ABCD内接于⊙O,若∠ADC=130°,则∠AOC的大小为度.
12. 如图,四边形ABCD内接于⊙O,若∠ADC=130°,则∠AOC的大小为度.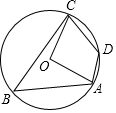 13. 如图,在Rt△ABC中,∠ACB=90°,BC=9,AC=12.分别以点A和点B为圆心、大于AB一半的长为半径作圆弧,两弧相交于点E和点F,作直线EF交AB于点D,连结CD.则CD的长为 .
13. 如图,在Rt△ABC中,∠ACB=90°,BC=9,AC=12.分别以点A和点B为圆心、大于AB一半的长为半径作圆弧,两弧相交于点E和点F,作直线EF交AB于点D,连结CD.则CD的长为 .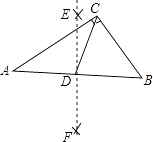 14. 如图,在平面直角坐标系中,抛物线y=x2﹣2x﹣1交y轴于点A,过点A作AB∥x轴交抛物线于点B,点P在抛物线上,连结PA、PB,若点P关于x轴的对称点恰好落在直线AB上,则△ABP的面积是.
14. 如图,在平面直角坐标系中,抛物线y=x2﹣2x﹣1交y轴于点A,过点A作AB∥x轴交抛物线于点B,点P在抛物线上,连结PA、PB,若点P关于x轴的对称点恰好落在直线AB上,则△ABP的面积是.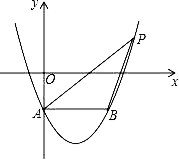
三、解答题
-
15. 小明解方程 =3出现了错误,解答过程如下:
方程两边都乘以(x-2),得1-(1-x)=3(第一步)
去括号,得1-1+x=3(第二步)
移项,合并同类项,得x=3(第三步)
检验,当x=3时x-2≠0(第四步)
所以x=3是原方程的解.(第五步)
(1)、小明解答过程是从第步开始出错的,原方程化为第一步的根据是.(2)、请写出此题正确的解答过程.16. 某校对初三学生进行物理、化学实验操作能力测试.物理、化学各有3个不同的操作实验题目,物理实验分别用①、②、③表示,化学实验分别用a、b、c表示.测试时每名学生每科只操作一个实验,实验的题目由学生抽签确定,第一次抽签确定物理实验题目,第二次抽签确定化学实验题目.王刚同学对物理的①、②号实验和化学的b、c号实验准备得较好.请用画树状图(或列表)的方法,求王刚同学同时抽到两科都准备得较好的实验题目的概率.
17. 定义:有一组对边相等而另一组对边不相等的凸四边形叫做“等对边四边形”.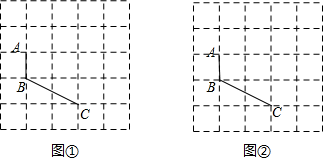 (1)、已知:图①、图②是5×5的正方形网格,线段AB、BC的端点均在格点上.在图①、图②中,按要求以AB、BC为边各画一个等对边四边形ABCD.
(1)、已知:图①、图②是5×5的正方形网格,线段AB、BC的端点均在格点上.在图①、图②中,按要求以AB、BC为边各画一个等对边四边形ABCD.要求:四边形ABCD的顶点D在格点上,且两个四边形不全等.
(2)、若每个小正方形网格的边长为一个单位,请直接写出(1)问中所画每个等对边四边形ABCD的面积.18. 我国古代数学名著《孙子算经》中记载了一道题,大意如下:100匹马恰好拉了100片瓦,已知1匹大马能拉3片瓦,3匹小马能拉1片瓦,问大马和小马各有多少匹?请解答上述问题.19. 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F.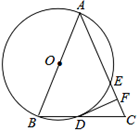 (1)、求证:DF⊥AC;(2)、若⊙O的半径为4,∠CDF=22.5°,请直接写出弧AE的长.20. 为弘扬中华传统文化,某校组织七年级800名学生参加诗词大赛,为了解学生整体的诗词积累情况,随机抽取部分学生的成绩(得分取正整数,满分为100分)进行统计分析,请根据尚未完成的列图表,解答问题:
(1)、求证:DF⊥AC;(2)、若⊙O的半径为4,∠CDF=22.5°,请直接写出弧AE的长.20. 为弘扬中华传统文化,某校组织七年级800名学生参加诗词大赛,为了解学生整体的诗词积累情况,随机抽取部分学生的成绩(得分取正整数,满分为100分)进行统计分析,请根据尚未完成的列图表,解答问题: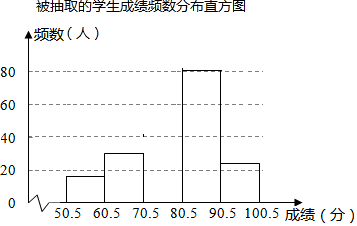
组别
分数段
频数
频率
一
50.5~60.5
16
0.08
二
60.5~70.5
40
0.20
三
70.5~80.5
50
0.25
四
80.5~90.5
m
0.35
五
90.5~100.5
24
n
(1)、本次抽样中,表中m= , n= , 样本成绩的中位数落在第组内.(2)、补全频数分布直方图.(3)、若规定成绩超过80分为优秀,请估计该校七年级学生中诗词积累成绩为优秀的人数.21. 在一条笔直的公路上依次有A、B、C三地,自行车爱好者甲、乙两人分别从A、B两地同时出发,沿直线匀速骑向C地.已知甲的速度为20km/h,如图所示,甲、乙两人与A地的距离y(km)与行驶时间x(h)的函数图象分别为线段OD、EF.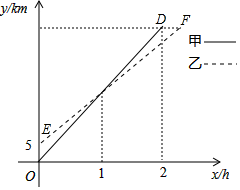 (1)、A、B两地的距离为km.(2)、求线段EF所在直线对应的函数关系式.(3)、若两人在出发时都配备了通话距离为3km的对讲机,求甲、乙两人均在骑行过程中可以用对讲机通话的时间段.22. (感知)如图①,四边形ABCD、CEFG均为正方形.可知BE=DG.
(1)、A、B两地的距离为km.(2)、求线段EF所在直线对应的函数关系式.(3)、若两人在出发时都配备了通话距离为3km的对讲机,求甲、乙两人均在骑行过程中可以用对讲机通话的时间段.22. (感知)如图①,四边形ABCD、CEFG均为正方形.可知BE=DG.(拓展)如图②,四边形ABCD、CEFG均为菱形,且∠A=∠F.求证:BE=DG.
(应用)如图③,四边形ABCD、CEFG均为菱形,点E在边AD上,点G在AD延长线上.若AE=2ED,∠A=∠F,△EBC的面积为8,菱形CEFG的面积是 .(只填结果)
 23. 如图①,在△ABC中,∠C=90°,AC=8cm,BC=6cm.动点P在线段AC上以5cm/s的速度从点A运动到点C.过点P作PD⊥AB于点D,将△APD绕PD的中点旋转180°得到△A'DP.设点P的运动时间为x(s).
23. 如图①,在△ABC中,∠C=90°,AC=8cm,BC=6cm.动点P在线段AC上以5cm/s的速度从点A运动到点C.过点P作PD⊥AB于点D,将△APD绕PD的中点旋转180°得到△A'DP.设点P的运动时间为x(s).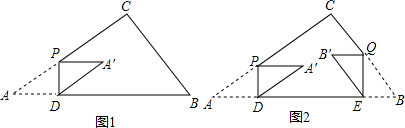 (1)、求点A'落在边BC上时x的值.(2)、设△A'DP和△ABC重叠部分图形周长为y(cm),求y与x之间的函数关系式.(3)、如图②,另有一动点Q与点P同时出发,在线段BC上以5cm/s的速度从点B运动到点C.过点Q作QE⊥AB于点E,将△BQE绕QE的中点旋转180°得到△B'EQ.连结A′B′.当直线A'B'与△ABC的边垂直或平行时,直接写出x的值.24. 定义:在平面直角坐标系中,将点P绕点T(t,0)(1>0)旋转180°得到点Q,则称点Q为点P的“发展点”.(1)、当t=2时,点(0,0)的“发展点”坐标为 , 点(-1,-1)的“发展点”坐标为.(2)、若t>3,则点(3,4)的“发展点”的横坐标为(用含t的代数式表示).(3)、若点P在直线y=2x+6上,其“发展点”Q在直线y=2x-8上,求点T的坐标.(4)、点P(3,3)在抛物线y=-x2+k上,点M在这条抛物线上,点Q为点P的“发展点”.若△PMQ是以点M为直角顶点的等腰直角三角形,求t的值.
(1)、求点A'落在边BC上时x的值.(2)、设△A'DP和△ABC重叠部分图形周长为y(cm),求y与x之间的函数关系式.(3)、如图②,另有一动点Q与点P同时出发,在线段BC上以5cm/s的速度从点B运动到点C.过点Q作QE⊥AB于点E,将△BQE绕QE的中点旋转180°得到△B'EQ.连结A′B′.当直线A'B'与△ABC的边垂直或平行时,直接写出x的值.24. 定义:在平面直角坐标系中,将点P绕点T(t,0)(1>0)旋转180°得到点Q,则称点Q为点P的“发展点”.(1)、当t=2时,点(0,0)的“发展点”坐标为 , 点(-1,-1)的“发展点”坐标为.(2)、若t>3,则点(3,4)的“发展点”的横坐标为(用含t的代数式表示).(3)、若点P在直线y=2x+6上,其“发展点”Q在直线y=2x-8上,求点T的坐标.(4)、点P(3,3)在抛物线y=-x2+k上,点M在这条抛物线上,点Q为点P的“发展点”.若△PMQ是以点M为直角顶点的等腰直角三角形,求t的值.