吉林省长春汽车经济技术开发区毕业班2019届数学中考一模试卷
试卷更新日期:2019-06-17 类型:中考模拟
一、单选题
-
1. 计算 的结果是( )A、 B、 C、 D、2. 从2019年起,长春市开始了城市轨道交通第三期建设,在建设规划中未来长春市城市轨道交通总长度将达到460000米,460000这个数字用科学记数法表示为( )A、4.6×104 B、46×104 C、4.6×105 D、4.6×1063. 下列立体图形中,主视图是矩形的是( )A、
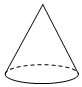 B、
B、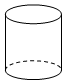 C、
C、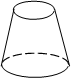 D、
D、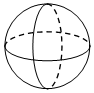 4. 使不等式2x﹣4≥0成立的最小整数是( )A、﹣2 B、0 C、2 D、35. 《九章算术》是我国古代的数学名著,书中的“折竹抵地”问题:今有竹高一丈,末折抵地,去本三尺.问折者高几何?意思是:一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部3尺远,问折断处离地面的高度是多少?设折断后离地面的高度为x尺,则可列方程为( )A、x2–3=(10–x)2 B、x2–32=(10–x)2 C、x2+3=(10–x)2 D、x2+32=(10–x)26. 如图,直线 ,若 , ,则 的大小为( )
4. 使不等式2x﹣4≥0成立的最小整数是( )A、﹣2 B、0 C、2 D、35. 《九章算术》是我国古代的数学名著,书中的“折竹抵地”问题:今有竹高一丈,末折抵地,去本三尺.问折者高几何?意思是:一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部3尺远,问折断处离地面的高度是多少?设折断后离地面的高度为x尺,则可列方程为( )A、x2–3=(10–x)2 B、x2–32=(10–x)2 C、x2+3=(10–x)2 D、x2+32=(10–x)26. 如图,直线 ,若 , ,则 的大小为( )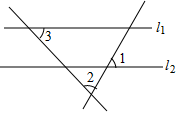 A、 B、 C、 D、7. 如图,为了保证道路交通安全,某段高速公路在A处设立观测点,与高速公路的距离AC为20米.现测得一辆小轿车从B处行驶到C处所用的时间为4秒.若∠BAC=α,则此车的速度为( )
A、 B、 C、 D、7. 如图,为了保证道路交通安全,某段高速公路在A处设立观测点,与高速公路的距离AC为20米.现测得一辆小轿车从B处行驶到C处所用的时间为4秒.若∠BAC=α,则此车的速度为( )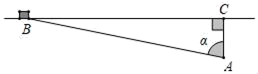 A、5tanα米/秒 B、80tanα米/秒 C、 米/秒 D、 米/秒8. 如图,在平面直角坐标系中,菱形OABC的顶点A在x轴的正半轴上,顶点B在函数y= (x>0)的图象上,若∠C=60°,AB=2,则k的值为( )
A、5tanα米/秒 B、80tanα米/秒 C、 米/秒 D、 米/秒8. 如图,在平面直角坐标系中,菱形OABC的顶点A在x轴的正半轴上,顶点B在函数y= (x>0)的图象上,若∠C=60°,AB=2,则k的值为( ) A、 B、 C、1 D、2
A、 B、 C、1 D、2二、填空题
-
9. 比较大小:2 .(填“>”、“=”或“<“)10. 计算: .11. 如图,AB为⊙O的直径,△PAB的边PA,PB与⊙O的交点分别为C、D.若 ,则∠P的大小为度.
 12. 如图,在 中, , 为 边上的中线,过点 作 交 于点 .若 , ,则 的长为.
12. 如图,在 中, , 为 边上的中线,过点 作 交 于点 .若 , ,则 的长为.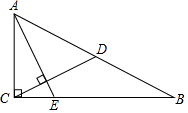 13. 如图,在平面直角坐标系中,点 、 、 、 依次在 轴上,点 、 的坐标分别是 、 .以点 为圆心, 长为半径画弧,再以点 为圆心, 长为半径画弧,两弧相交于点 ,测得 , .则点 的横坐标是.
13. 如图,在平面直角坐标系中,点 、 、 、 依次在 轴上,点 、 的坐标分别是 、 .以点 为圆心, 长为半径画弧,再以点 为圆心, 长为半径画弧,两弧相交于点 ,测得 , .则点 的横坐标是.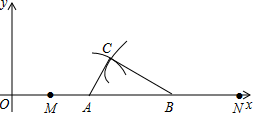 14. 如图,在平面直角坐标系中,点O是边长为2的正方形ABCD的中心.函数y=(x﹣h)2的图象与正方形ABCD有公共点,则h的取值范围是.
14. 如图,在平面直角坐标系中,点O是边长为2的正方形ABCD的中心.函数y=(x﹣h)2的图象与正方形ABCD有公共点,则h的取值范围是.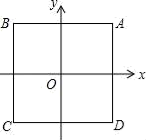
三、解答题
-
15. 先化简再求值:( + )÷ ,其中:x= .16. 如图,现有三张不透明的卡片,卡片的正面分别标有字母 、 、 ,每张卡片除字母不同之外,其余均相同.将三张卡片背面向上洗匀,从中随机抽取一张,记下字母后放回,重新洗匀,再从中随机抽取一张.请用画树状图(或列表)的方法,求两次抽出的卡片上的字母相同的概率.
 17. 小欢和小乐一起去超市购买同一种矿泉水和同一种面包,小欢买了3瓶矿泉水和3个面包共花21元钱;小乐买了4瓶矿泉水和5个面包共花32.5元钱.求此种矿泉水和面包的单价.18. 图①、图②均是边长为1的小正方形组成的5X5的网格,每个小正方形的顶点称为格点线段AB的端点均在格点上.
17. 小欢和小乐一起去超市购买同一种矿泉水和同一种面包,小欢买了3瓶矿泉水和3个面包共花21元钱;小乐买了4瓶矿泉水和5个面包共花32.5元钱.求此种矿泉水和面包的单价.18. 图①、图②均是边长为1的小正方形组成的5X5的网格,每个小正方形的顶点称为格点线段AB的端点均在格点上.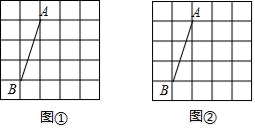 (1)、在图①中作正方形ABCD,正方形ABCD的面积为(2)、在图②中作Rt△ABM,使点M在格点上,且sin∠BAM=19. 如图, 是 的直径,点 、 在 上,过点 作 的切线交 的延长线于点 .已知 得半径为 , .
(1)、在图①中作正方形ABCD,正方形ABCD的面积为(2)、在图②中作Rt△ABM,使点M在格点上,且sin∠BAM=19. 如图, 是 的直径,点 、 在 上,过点 作 的切线交 的延长线于点 .已知 得半径为 , .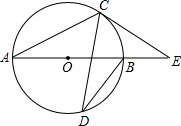 (1)、求 的度数.(2)、求 的长.(结果保留 )20. 某校开展“走进中国数学史”为主题的知识竞赛活动,八、九年级各有200名学生参加竞赛,为了解这两个年级参加竞赛学生的成绩情况,从中各随机抽取20名学生的成绩,数据如下:
(1)、求 的度数.(2)、求 的长.(结果保留 )20. 某校开展“走进中国数学史”为主题的知识竞赛活动,八、九年级各有200名学生参加竞赛,为了解这两个年级参加竞赛学生的成绩情况,从中各随机抽取20名学生的成绩,数据如下:八年级
91
89
77
86
71
九年级
84
93
66
69
76
51
97
93
72
91
87
77
82
85
88
81
92
85
85
95
90
88
67
88
91
88
88
90
64
91
96
68
97
99
88
整理上面数据,得到如下统计表:
成绩
人数
年级
八年级
1
1
3
7
8
九年级
0
4
2
8
6
样本数据的平均数、中位数、众数、方差如下表所示:
统计表
年级
平均数
中位数
众数
方差
八年级
83.85
88
91
127.03
九年级
83.95
87.5
99.45
根据以上信息,回答下列问题:
(1)、写出上表中众数 的值.(2)、试估计八、九年级这次选拔成绩80分以上的人数和.(3)、你认为哪个年级学生的竞赛成绩较好?说明你的理由.(至少从两个不同的角度说明推断的合理性)21. 某工地需要利用炸药实施爆破,操作人员点燃导火线后,要在炸药爆炸前跑到300米以外的安全区域,炸药导火线的长度y(厘米)与燃烧的时间x(秒)之间的函数关系如图所示. (1)、请写出点B的实际意义,(2)、求y与x之间的函数关系式,并写出自变量的取值范围.(3)、问操作人员跑步的速度必须超过多少,才能保证安全.22. 已知 , ,直线 经过点 ,作 ,垂足为 ,连接 .
(1)、请写出点B的实际意义,(2)、求y与x之间的函数关系式,并写出自变量的取值范围.(3)、问操作人员跑步的速度必须超过多少,才能保证安全.22. 已知 , ,直线 经过点 ,作 ,垂足为 ,连接 .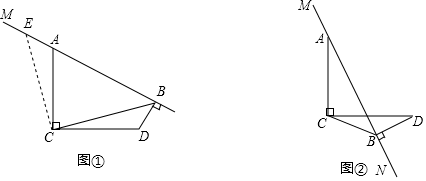 (1)、【感知】如图①,点 、 在 同侧,且点 在 右侧,在射线 上截取 ,连接 ,可证 ,从而得出 , ,进而得出 度.(2)、【探究】如图②,当点 、 在 异侧时,(感知)得出的 的大小是否改变?若不改变,给出证明;若改变,请求出 的大小.(3)、【应用】在直线 绕点 旋转的过程中,当 , 时,直接写出 的长.23. 如图①,在菱形 中, , .点 从点 出发以每秒2个单位的速度沿边 向终点 运动,过点 作 交边 于点 ,过点 向上作 ,且 ,以 、 为边作矩形 .设点 的运动时间为 (秒),矩形 与菱形 重叠部分图形的面积为 .
(1)、【感知】如图①,点 、 在 同侧,且点 在 右侧,在射线 上截取 ,连接 ,可证 ,从而得出 , ,进而得出 度.(2)、【探究】如图②,当点 、 在 异侧时,(感知)得出的 的大小是否改变?若不改变,给出证明;若改变,请求出 的大小.(3)、【应用】在直线 绕点 旋转的过程中,当 , 时,直接写出 的长.23. 如图①,在菱形 中, , .点 从点 出发以每秒2个单位的速度沿边 向终点 运动,过点 作 交边 于点 ,过点 向上作 ,且 ,以 、 为边作矩形 .设点 的运动时间为 (秒),矩形 与菱形 重叠部分图形的面积为 . (1)、用含 的代数式表示线段 的长.(2)、当点 落在边 上时,求 的值.(3)、当 时,求 与 之间的函数关系式,(4)、如图②,若点 是 的中点,作直线 .当直线 将矩形 分成两部分图形的面积比为 时,直接写出 的值24. 在平面直角坐标系中,函数 的图像记为 ,函数 的图像记为 ,其中 为常数,且 ,图像 、 ,合起来得到的图像标记为 .(1)、求图像 与 轴的交点坐标.(2)、当图像 的最低点到 轴距离为3时,求 的值.(3)、当 时,若点 在图像 上,求 的值.(4)、点 、 的坐标分别为 、 ,连接 与图像 有两个交点时 的取值范围.
(1)、用含 的代数式表示线段 的长.(2)、当点 落在边 上时,求 的值.(3)、当 时,求 与 之间的函数关系式,(4)、如图②,若点 是 的中点,作直线 .当直线 将矩形 分成两部分图形的面积比为 时,直接写出 的值24. 在平面直角坐标系中,函数 的图像记为 ,函数 的图像记为 ,其中 为常数,且 ,图像 、 ,合起来得到的图像标记为 .(1)、求图像 与 轴的交点坐标.(2)、当图像 的最低点到 轴距离为3时,求 的值.(3)、当 时,若点 在图像 上,求 的值.(4)、点 、 的坐标分别为 、 ,连接 与图像 有两个交点时 的取值范围.