吉林省长春德惠市2019届九年级4月质量监测数学试卷
试卷更新日期:2019-06-17 类型:中考模拟
一、单选题
-
1. 计算 的结果是( )A、 B、 C、 D、2. 近年来,国家重视精准扶贫,收效显著,据统计约 人脱贫, 用科学记数法可表示为( )A、 B、 C、 D、3. 如图所示是由四个大小相同的正方体组成的几何体,那么它的主视图是( )
 A、
A、 B、
B、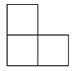 C、
C、 D、
D、 4. 不等式4﹣2x>0的解集在数轴上表示为( )A、
4. 不等式4﹣2x>0的解集在数轴上表示为( )A、 B、
B、 C、
C、 D、
D、 5. 如图,在▱ABCD中,连接AC,∠ABC=∠CAD=45°,AB= , 则BC的长是( )
5. 如图,在▱ABCD中,连接AC,∠ABC=∠CAD=45°,AB= , 则BC的长是( ) A、 B、2 C、2 D、46. 关于 的一元二次方程 有两个相等的实数根,那么 的值是( )A、 B、 C、 D、7. 如图,点 , , , 在 上, ,点 是 的中点,则 的度数是( )
A、 B、2 C、2 D、46. 关于 的一元二次方程 有两个相等的实数根,那么 的值是( )A、 B、 C、 D、7. 如图,点 , , , 在 上, ,点 是 的中点,则 的度数是( )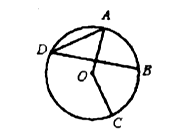 A、 B、 C、 D、8. 如图,直角三角形的直角顶点在坐标原点,∠OAB=30°,若点A在反比例函数y= (x>0)的图象上,则经过点B的反比例函数解析式为( )
A、 B、 C、 D、8. 如图,直角三角形的直角顶点在坐标原点,∠OAB=30°,若点A在反比例函数y= (x>0)的图象上,则经过点B的反比例函数解析式为( )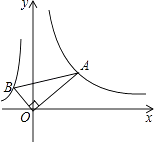 A、y=﹣ B、y=﹣ C、y=﹣ D、y=
A、y=﹣ B、y=﹣ C、y=﹣ D、y=二、填空题
-
9. 与 最接近的整数为.10. 分解因式: .11. 如图,在菱形ABCD中,若AC=6,BD=8,则菱形ABCD的面积是.
 12. 如图,△ABC的两条中线AD和BE相交于点G,过点E作EF∥BC交AD于点F,那么 =.
12. 如图,△ABC的两条中线AD和BE相交于点G,过点E作EF∥BC交AD于点F,那么 =.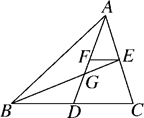 13. 如图,在边长为4的正方形ABCD中,以点B为圆心,以AB为半径画弧,交对角线BD于点E,则图中阴影部分的面积是(结果保留π)
13. 如图,在边长为4的正方形ABCD中,以点B为圆心,以AB为半径画弧,交对角线BD于点E,则图中阴影部分的面积是(结果保留π)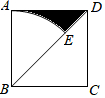 14. 如图,已知正方形 中, ,有一抛物线 向上平移 个单位( )与正方形 的边(包括四个顶点)有交点,则 的取值范围是.
14. 如图,已知正方形 中, ,有一抛物线 向上平移 个单位( )与正方形 的边(包括四个顶点)有交点,则 的取值范围是.
三、解答题
-
15. 先化简,再求值: ,其中 .16. 中华文化,源远流长,在文学方面,《西游记》、《三国演义》、《水浒传》、《红楼梦》被称为“四大古典名著”,是我国古代长篇小说的经典代表,小花和等等两名同学,准备从这四大名著中各自随机选择一部来阅读,请你用画树状图(或列表)的方法,求他们选中同一名著的概率.17. 春节期间,收发微信红包已经成为各类人群进行交流联系、增强感情的一部分,小王在 年春节共收到红包 元, 年春节共收到红包 元,求小王在这两年春节收到红包的年平均增长率.18. 如图,一块纸片 ,现在进行如下操作:以点 为圆心,适当长为半径画弧,分别交 于点 ;在分别以 为圆心,大于 的长为半径画弧,两弧在 内部相交于点 ,画射线 ,交 与点 .
 (1)、求证: .(2)、若 ,求 的度数.19. 某政治老师为了解学生对“社会主义核心价值观”的知晓程度,采取随机抽样的方式进行问卷调查,调查结果分为“ 非常了解”、“ 了解”、“ 基本了解”三个等级,并根据调查结果绘制了如下两幅不完整的统计图.
(1)、求证: .(2)、若 ,求 的度数.19. 某政治老师为了解学生对“社会主义核心价值观”的知晓程度,采取随机抽样的方式进行问卷调查,调查结果分为“ 非常了解”、“ 了解”、“ 基本了解”三个等级,并根据调查结果绘制了如下两幅不完整的统计图. (1)、这次调查的学生人数为人, , ;(2)、补全条形统计图;(3)、若该校约有学生 人,请你根据抽样调查的结果,估计该校大约有多少人对“社会主义核心价值观”达到“ 非常了解”的程度.20. 某物流公司引进A,B两种机器人用来搬运某种货物,这两种机器人充满电后可以连续搬运5小时,A种机器人于某日0时开始搬运,过了1小时,B种机器人也开始搬运,如图,线段OG表示A种机器人的搬运量yA(千克)与时间x(时)的函数图象,根据图象提供的信息,解答下列问题:
(1)、这次调查的学生人数为人, , ;(2)、补全条形统计图;(3)、若该校约有学生 人,请你根据抽样调查的结果,估计该校大约有多少人对“社会主义核心价值观”达到“ 非常了解”的程度.20. 某物流公司引进A,B两种机器人用来搬运某种货物,这两种机器人充满电后可以连续搬运5小时,A种机器人于某日0时开始搬运,过了1小时,B种机器人也开始搬运,如图,线段OG表示A种机器人的搬运量yA(千克)与时间x(时)的函数图象,根据图象提供的信息,解答下列问题: (1)、求yB关于x的函数解析式;(2)、如果A,B两种机器人连续搬运5小时,那么B种机器人比A种机器人多搬运了多少千克?21. 已知△ABC是等边三角形,四边形ADEF是菱形,∠ADE=120°(AD>AB).
(1)、求yB关于x的函数解析式;(2)、如果A,B两种机器人连续搬运5小时,那么B种机器人比A种机器人多搬运了多少千克?21. 已知△ABC是等边三角形,四边形ADEF是菱形,∠ADE=120°(AD>AB). (1)、如图①,当AD与边BC相交,点D与点F在直线AC的两侧时,BD与CF的数量关系为.(2)、将图①中的菱形ADEF绕点A在平面内逆时针旋转α(0°<α<180°).
(1)、如图①,当AD与边BC相交,点D与点F在直线AC的两侧时,BD与CF的数量关系为.(2)、将图①中的菱形ADEF绕点A在平面内逆时针旋转α(0°<α<180°).Ⅰ.判断(1)中的结论是否仍然成立,请利用图②证明你的结论.
Ⅱ.若AC=4,AD=6,当△ACE为直角三角形时,直接写出CE的长度.
22. 如图 ,在三角形ABC中, ,点D为边BC的中点,射线 交AB于点 点P从点D出发,沿射线DE以每秒1个单位长度的速度运动 以PD为斜边,在射线DE的右侧作等腰直角 设点P的运动时间为 秒 . (1)、用含t的代数式表示线段EP的长.(2)、求点Q落在边AC上时t的值.(3)、当点Q在 内部时,设 和 重叠部分图形的面积为 平方单位 ,求S与t之间的函数关系式.23. 给定一个函数,如果这个函数的图象上存在一个点,这个点的横、纵坐标相等,那么这个点叫做该函数的不变点.
(1)、用含t的代数式表示线段EP的长.(2)、求点Q落在边AC上时t的值.(3)、当点Q在 内部时,设 和 重叠部分图形的面积为 平方单位 ,求S与t之间的函数关系式.23. 给定一个函数,如果这个函数的图象上存在一个点,这个点的横、纵坐标相等,那么这个点叫做该函数的不变点. (1)、一次函数 的不变点的坐标为 .(2)、反比例函数 的不变点的坐标为 .(3)、二次函数 的两个不变点分别为点 ( 在 的左侧),将点 绕点 顺时针旋转 得到点 ,求点 的坐标.(4)、如图,已知函数 的两个不变点的坐标为A(-1,-1),B(3,3).设抛物线与线段 围成的封闭图形记作 .点 为一次函数 的不变点,以线段 为边向下作正方形 .当 两点中只有一个点在封闭图形 的内部(不包含边界)时,求出 的取值范围.
(1)、一次函数 的不变点的坐标为 .(2)、反比例函数 的不变点的坐标为 .(3)、二次函数 的两个不变点分别为点 ( 在 的左侧),将点 绕点 顺时针旋转 得到点 ,求点 的坐标.(4)、如图,已知函数 的两个不变点的坐标为A(-1,-1),B(3,3).设抛物线与线段 围成的封闭图形记作 .点 为一次函数 的不变点,以线段 为边向下作正方形 .当 两点中只有一个点在封闭图形 的内部(不包含边界)时,求出 的取值范围.