吉林省白山市2019届数学中考一模试卷
试卷更新日期:2019-06-17 类型:中考模拟
一、单选题
-
1. - 的相反数是( )A、- B、 C、 D、-2. 将一个机器零件按如图方式摆放,则它的俯视图为( )
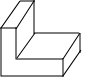 A、
A、 B、
B、 C、
C、 D、
D、 3. 计算 的结果为( )A、 B、 C、 D、4. 如图,直尺经过一块三角板DCB的顶点B, , ,则 的度数为( )
3. 计算 的结果为( )A、 B、 C、 D、4. 如图,直尺经过一块三角板DCB的顶点B, , ,则 的度数为( ) A、150° B、140° C、130° D、100°5. 如图,等边△ABC的边长为1cm,D、E分别AB、AC是上的点,将△ADE沿直线DE折叠,点A落在点A′处,且点A′在△ABC外部,则阴影部分的周长为( )cm.
A、150° B、140° C、130° D、100°5. 如图,等边△ABC的边长为1cm,D、E分别AB、AC是上的点,将△ADE沿直线DE折叠,点A落在点A′处,且点A′在△ABC外部,则阴影部分的周长为( )cm. A、1 B、2 C、3 D、46. 某家具生产厂家生产桌椅,已知每块板材可做桌子1张或椅子3把,现计划用100块这种板材生产一批桌椅(不考虑板材的损耗),设用x块板材做桌子,用y块板材做椅子,使得恰好配套(一张桌子配两把椅子),则下列方程组正确的是( )A、 B、 C、 D、
A、1 B、2 C、3 D、46. 某家具生产厂家生产桌椅,已知每块板材可做桌子1张或椅子3把,现计划用100块这种板材生产一批桌椅(不考虑板材的损耗),设用x块板材做桌子,用y块板材做椅子,使得恰好配套(一张桌子配两把椅子),则下列方程组正确的是( )A、 B、 C、 D、二、填空题
-
7. 测得某人的一根头发直径约为0.0000715米,将0.0000715用科学记数法表示为.8. 分解因式: .9. 计算 ﹣9 的结果是 .10. 若关于x的一元二次方程(2k﹣1)x2﹣6x+9=0没有实数根,则k的取值范围是.11. 如图, 中, ,按下列步骤作图:①分别以点A、C为圆心,大于 的长为半径画弧,两弧的交点分别为点F、G;②过点F、G作直线FG,交边AD于点E,若 的周长为11,则 的周长为.
 12. 如图,身高1.6米的小丽在阳光下的影长为2米,在同一时刻,一棵大树的影长为8米,则这棵树的高度为米.
12. 如图,身高1.6米的小丽在阳光下的影长为2米,在同一时刻,一棵大树的影长为8米,则这棵树的高度为米. 13. 如图, 经过正六边形ABCDEF的顶点A、E,则弧AE所对的圆周角 等于.
13. 如图, 经过正六边形ABCDEF的顶点A、E,则弧AE所对的圆周角 等于.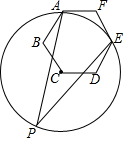 14. 如图抛物线 与直线 相交于点 、 ,与 轴交于点 ,若 为直角,则当 的时自变量 的取值范围是.
14. 如图抛物线 与直线 相交于点 、 ,与 轴交于点 ,若 为直角,则当 的时自变量 的取值范围是.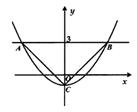 15. 已知在网格中每个小正方形的边长都是1,图1中的阴影图案是由一条对角线和以格点为圆心,半径为2的圆弧围成的弓形.
15. 已知在网格中每个小正方形的边长都是1,图1中的阴影图案是由一条对角线和以格点为圆心,半径为2的圆弧围成的弓形. (1)、图1中阴影部分的面积是(结果保留π);(2)、请你在图2中以图1为基本图案,借助轴对称,平移或旋转设计一个轴对称的花边图案(要求至少含有两种图形变换).
(1)、图1中阴影部分的面积是(结果保留π);(2)、请你在图2中以图1为基本图案,借助轴对称,平移或旋转设计一个轴对称的花边图案(要求至少含有两种图形变换).三、解答题
-
16. 先化简,再求值:(x+5)(x-1)+(x-2)2 , 其中x=-2.17. 因课外活动的需要,鵬胜同学第一次在文具店买若干支笔芯,花了30元,第二次再去买该款笔芯时,发现每支笔芯的价钱涨了0.1元,他这一次买该款笔芯的数量是第一次的2倍,花了68元,求他两次买的笔芯分别是多少支?18. 如图,在四边形ABCD中, , ,M是AB的中点.求证: .
 19. 甲、乙两人都握有分别标记为A、B、C的三张牌,两人做游戏,游戏规则是:若两人出的牌不同,则A胜B,B胜C,C胜A;若两人出的牌相同,则为平局.(1)、用树状图或列表等方法,列出甲、乙两人一次游戏的所有可能的结果;(2)、求出现平局的概率.
19. 甲、乙两人都握有分别标记为A、B、C的三张牌,两人做游戏,游戏规则是:若两人出的牌不同,则A胜B,B胜C,C胜A;若两人出的牌相同,则为平局.(1)、用树状图或列表等方法,列出甲、乙两人一次游戏的所有可能的结果;(2)、求出现平局的概率.
20. 如图是某市的一幢在建的楼,准备上市销售,该楼前有一座装有高压线的铁塔BC经过,市民想知道高压线的电辐射对居住是否有影响,则需要测量该楼到铁塔的水平距离DC的长以及铁塔BC的高度.为了安全,不能直接测量铁塔的高度.在该楼的楼顶A处测得铁塔的塔B的仰角过 ,测得铁塔的塔底C的俯角 ,该楼的高度 ,求铁塔BC的高度(参考数据: , , , ). 21. 如图,矩形ABCD的顶点A,B在x轴的正半轴上,反比例函数y= 在第一象限内的图象与直线y= x交于点D,且反比例函数y= 交BC于点E,AD=3.
21. 如图,矩形ABCD的顶点A,B在x轴的正半轴上,反比例函数y= 在第一象限内的图象与直线y= x交于点D,且反比例函数y= 交BC于点E,AD=3. (1)、求D点的坐标及反比例函数的关系式;(2)、若矩形的面积是24,请写出△CDE的面积(不需要写解答过程).22. 某校为了了解七年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组(A:39.5﹣46.5;B:46.5﹣53.5;C:53.5﹣60.5;D:60.5﹣67.5;E:67.5﹣74.5),并依据统计数据绘制了如下两幅尚不完整的统计图.
(1)、求D点的坐标及反比例函数的关系式;(2)、若矩形的面积是24,请写出△CDE的面积(不需要写解答过程).22. 某校为了了解七年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组(A:39.5﹣46.5;B:46.5﹣53.5;C:53.5﹣60.5;D:60.5﹣67.5;E:67.5﹣74.5),并依据统计数据绘制了如下两幅尚不完整的统计图.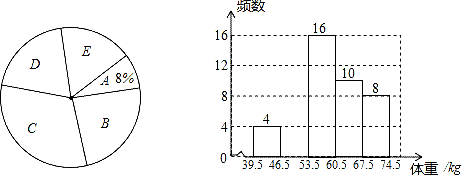
请解答下列问题:
(1)、这次随机抽取了名学生调查,并补全频数分布直方图;(2)、在抽取调查的若干名学生中体重在组的人数最多,在扇形统计图中D组的圆心角是度;(3)、请你估计该校七年级体重超过60kg的学生大约有多少名?23. 周末,甲、乙两名大学生骑自行车去距学校6000米的净月潭公园.两人同时从学校出发,以a米/分的速度匀速行驶.出发4.5分钟时,甲同学发现忘记带学生证,以1.5a米/分的速度按原路返回学校,取完学生证(在学校取学生证所用时间忽略不计),继续以返回时的速度追赶乙.甲追上乙后,两人以相同的速度前往净月潭.乙骑自行车的速度始终不变.设甲、乙两名大学生距学校的路程为s(米),乙同学行驶的时间为t(分),s与t之间的函数图象如图所示.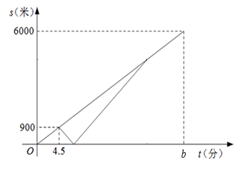 (1)、求a、b的值.(2)、求甲追上乙时,距学校的路程.(3)、当两人相距500米时,直接写出t的值是.24. 如图,在矩形ABCD中, , ,将矩形沿直线EF折叠.使得点A恰好落在BC边上的点G处,且点E、F分别在边AB、AD上(含端点),连接CF.
(1)、求a、b的值.(2)、求甲追上乙时,距学校的路程.(3)、当两人相距500米时,直接写出t的值是.24. 如图,在矩形ABCD中, , ,将矩形沿直线EF折叠.使得点A恰好落在BC边上的点G处,且点E、F分别在边AB、AD上(含端点),连接CF. (1)、当 时,求AE的长;(2)、当AF取得最小值时,求折痕EF的长;(3)、连接CF,当 是以CG为底的等腰三角形时,直接写出BG的长.25. 如图,在 中, , , ,四边形PDEF是矩形, , .矩形PDEF从点B出发,沿射线BC以每秒1个单位长度的速度向点C运动,同时点Q从点P出发,沿折线P-D-E以每秒1个单位长度的速度匀速运动,当点Q到达点E时,点Q与矩形PDEF同时停止运动,连接QC,设点Q的运动时间为t秒( ).
(1)、当 时,求AE的长;(2)、当AF取得最小值时,求折痕EF的长;(3)、连接CF,当 是以CG为底的等腰三角形时,直接写出BG的长.25. 如图,在 中, , , ,四边形PDEF是矩形, , .矩形PDEF从点B出发,沿射线BC以每秒1个单位长度的速度向点C运动,同时点Q从点P出发,沿折线P-D-E以每秒1个单位长度的速度匀速运动,当点Q到达点E时,点Q与矩形PDEF同时停止运动,连接QC,设点Q的运动时间为t秒( ). (1)、求线段PC的长(用含t的代数式表示);(2)、当点Q落在AB边上时,求t的值;(3)、设 的面积为S,求S与t之间的函数关系式;(4)、当四边形PDEF与 重叠部分图形为五边形时,直接写出使 为直角三角形时t的取值范围.26. 如图,在平面直角坐标系中,把抛物线 先向右平移1个单位长度,再向下平移4个单位长度,得到抛物线 ,所得抛物线与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,顶点为M.
(1)、求线段PC的长(用含t的代数式表示);(2)、当点Q落在AB边上时,求t的值;(3)、设 的面积为S,求S与t之间的函数关系式;(4)、当四边形PDEF与 重叠部分图形为五边形时,直接写出使 为直角三角形时t的取值范围.26. 如图,在平面直角坐标系中,把抛物线 先向右平移1个单位长度,再向下平移4个单位长度,得到抛物线 ,所得抛物线与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,顶点为M. (1)、写出h、k的值及点A、B的坐标;(2)、判断 的形状,并计算其面积;(3)、点P是抛物线上的一动点,在y轴上存在点Q,使以点A、B、P、Q为顶点组成的四边形是平行四边形,求点P的坐标.
(1)、写出h、k的值及点A、B的坐标;(2)、判断 的形状,并计算其面积;(3)、点P是抛物线上的一动点,在y轴上存在点Q,使以点A、B、P、Q为顶点组成的四边形是平行四边形,求点P的坐标.