吉林省白山市2019届数学中考二模试卷
试卷更新日期:2019-06-17 类型:中考模拟
一、单选题
-
1. (﹣1)3等于( )A、﹣1 B、1 C、﹣3 D、32. 人体中红细胞的直径约为0.0000075m,用科学记数法表示这个数为( )A、7.5×106 B、75×10﹣7 C、7.5×10﹣6 D、0.75×10﹣53. 如图,已知AB为⊙O的直径,∠ABD=20°,则∠BCD等于( )
 A、80° B、70° C、60° D、50°4. 如图,在△ABC中,D、E分别在AB,AC上,DE∥BC,且AD:DB=3:2,则S△ADE:S四边形DECB为( )
A、80° B、70° C、60° D、50°4. 如图,在△ABC中,D、E分别在AB,AC上,DE∥BC,且AD:DB=3:2,则S△ADE:S四边形DECB为( ) A、3:2 B、3:5 C、9:25 D、9:165. 如图,A为双曲线y= 上任意一点,过点A作轴的垂线,交双曲线y=﹣ 于点B,连结OA,OB,则△AOB的面积等于( )
A、3:2 B、3:5 C、9:25 D、9:165. 如图,A为双曲线y= 上任意一点,过点A作轴的垂线,交双曲线y=﹣ 于点B,连结OA,OB,则△AOB的面积等于( )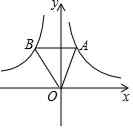 A、 B、 C、3 D、66. 下列几何体是由4个相同的小正方体搭成的,其中主视图和左视图相同的是( )
A、 B、 C、3 D、66. 下列几何体是由4个相同的小正方体搭成的,其中主视图和左视图相同的是( )
A、 B、
B、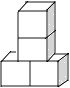 C、
C、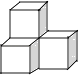 D、
D、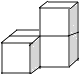 7. 把多项式x2+(p﹣q)x﹣pq分解因式,结果正确的是( )A、(x+p)(x+q) B、(x﹣p)(x﹣q) C、(x+p)(x﹣q) D、(x﹣p)(x+q)8. 若一个扇形的弧长l= ,面积S=2π,则这个扇形的圆心角为( )A、50° B、60° C、70° D、80°
7. 把多项式x2+(p﹣q)x﹣pq分解因式,结果正确的是( )A、(x+p)(x+q) B、(x﹣p)(x﹣q) C、(x+p)(x﹣q) D、(x﹣p)(x+q)8. 若一个扇形的弧长l= ,面积S=2π,则这个扇形的圆心角为( )A、50° B、60° C、70° D、80°二、填空题
-
9. 计算:(﹣2a)2•a=.10. 关于x的一元二次方程2x2﹣3x+m=0有两个相等的实数根,则实数m=.11. 不等式组 的解集是.12. 如图,在△ABC中,OB,OC分别为∠ABC和∠ACB的平分线,且∠A=70°,则∠BOC=.
 13. 如图,四边形AOBC为平行四边形,点A的坐标为(2,3),点B的坐标为(4,1),则点C坐标为.
13. 如图,四边形AOBC为平行四边形,点A的坐标为(2,3),点B的坐标为(4,1),则点C坐标为. 14. 如图,点A的坐标为(﹣1,0),点C在y轴的正半轴上,点B在第一象限,CB∥x轴,且CA=CB,若抛物线y=a(x﹣1)2+k经过A,B,C三点,则此抛物线的解析式为.
14. 如图,点A的坐标为(﹣1,0),点C在y轴的正半轴上,点B在第一象限,CB∥x轴,且CA=CB,若抛物线y=a(x﹣1)2+k经过A,B,C三点,则此抛物线的解析式为.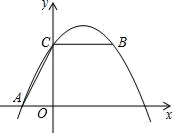
三、解答题
-
15. 先化简,再求值:(a+2b)(a﹣2b)+(a﹣2b)2﹣2a(a﹣b),其中a=6,b=16. 一只不透明袋子中装有1个红球、2个黄球,这些球除颜色外都相同。小明搅匀后从中意摸出一个球,记录颜色后放回、搅匀,再从中任意摸出1个球。用画树状图或列表法列出摸出球的所有等可能情况,并求两次摸出的球都是红球的概率。17. 某工厂计划在规定时间内生产24000个零件,若每天比原计划多生产30个零件,则在规定时间内可以多生产300个零件.求原计划每天生产的零件个数和规定的天数.18. 国家规定,中小学生每天在校体育活动时间不低于1小时,为了解这项政策的落实情况,有关部门就“你某天在校体育活动时间是多少”的问题,在某校随机抽查了部分学生,再根据活动时间t(小时)进行分组(A组:t<0.5,B组:0.5≤t<1,C组:1≤t<1.5,D组:t≥1.5),绘制成如下两幅不完整统计图,请根据图中信息回答问题:
 (1)、此次抽查的学生数为人,并补全条形统计图;(2)、从抽查的学生中随机询问一名学生,该生当天在校体育活动时间低于1小时的概率是;(3)、若当天在校学生数为1200人,请估计在当天达到国家规定体育活动时间的学生有人.19. 如图,AB为⊙O直径,点C在⊙O上,点D在AB的延长线上,∠BCD=∠CAD
(1)、此次抽查的学生数为人,并补全条形统计图;(2)、从抽查的学生中随机询问一名学生,该生当天在校体育活动时间低于1小时的概率是;(3)、若当天在校学生数为1200人,请估计在当天达到国家规定体育活动时间的学生有人.19. 如图,AB为⊙O直径,点C在⊙O上,点D在AB的延长线上,∠BCD=∠CAD (1)、求证:DC为⊙O的切线;(2)、若AB=4,DB=1,则CD=.20. 如图,已知灯塔P的周围10海里的范围内有暗礁,一艘渔轮在A处测得灯塔P在北偏东60°的方向,向正东航行8海里到B处后,又测得该灯塔在北偏东45°方向,渔轮不改变方向,继续向东航行,有没有触礁危险?请通过计算说明理由.(参考数据: =1.732, =1.414)
(1)、求证:DC为⊙O的切线;(2)、若AB=4,DB=1,则CD=.20. 如图,已知灯塔P的周围10海里的范围内有暗礁,一艘渔轮在A处测得灯塔P在北偏东60°的方向,向正东航行8海里到B处后,又测得该灯塔在北偏东45°方向,渔轮不改变方向,继续向东航行,有没有触礁危险?请通过计算说明理由.(参考数据: =1.732, =1.414) 21. 如图,在△ABC中,P为平面内一点,连结PA,PB,PC,分别以PC和AC为一边向右作等边三角形△PCM和△ACD.
21. 如图,在△ABC中,P为平面内一点,连结PA,PB,PC,分别以PC和AC为一边向右作等边三角形△PCM和△ACD. (1)、【探究】求证:PM=PC,MD=PA(2)、【应用】若BC=a,AC=b,∠ACB=60°,则PA+PB+PC的最小值是(用a,b表示)22. 为营造书香家庭,周末小亮和姐姐一起从家出发去图书馆借书,走了6分钟忘带借书证,小亮立即骑路边共享单车返回家中取借书证,姐姐以原来的速度继续向前行走,小亮取到借书证后骑单车原路原速前往图书馆,小亮追上姐姐后用单车带着姐姐一起前往图书馆已知单车的速度是步行速度的3倍,如图是小亮和姐姐距家的路程y(米)与姐姐出发时间x(分钟)的函数图象,根据图象解答下列问题:
(1)、【探究】求证:PM=PC,MD=PA(2)、【应用】若BC=a,AC=b,∠ACB=60°,则PA+PB+PC的最小值是(用a,b表示)22. 为营造书香家庭,周末小亮和姐姐一起从家出发去图书馆借书,走了6分钟忘带借书证,小亮立即骑路边共享单车返回家中取借书证,姐姐以原来的速度继续向前行走,小亮取到借书证后骑单车原路原速前往图书馆,小亮追上姐姐后用单车带着姐姐一起前往图书馆已知单车的速度是步行速度的3倍,如图是小亮和姐姐距家的路程y(米)与姐姐出发时间x(分钟)的函数图象,根据图象解答下列问题: (1)、小亮骑共享单车返回家所用的时间是分钟,他骑共享单车从家到图书馆所用的时间为分钟.(2)、求小亮骑共享单车从家出发去图书馆时距家的路程y(米)与姐姐出发时间x(分钟)之间的函数关系式;(3)、当小亮追上姐姐时,他距图书馆的路程是米.23. 如图,四边形ABCD为矩形,AB=4cm,AD=3cm,点P从点A出发,以2cm/s的速度沿折线AD﹣DB向终点B运动,点Q从点B出发,以1cm/s的速度沿折线BC﹣CD向终点D运动.点P,Q两点同时出发,当一点到达终点时,另一点也随之停止,设运动的时间为ts,△PDQ的面积为Scm2(规定:线段是面积为0的特殊三角形)
(1)、小亮骑共享单车返回家所用的时间是分钟,他骑共享单车从家到图书馆所用的时间为分钟.(2)、求小亮骑共享单车从家出发去图书馆时距家的路程y(米)与姐姐出发时间x(分钟)之间的函数关系式;(3)、当小亮追上姐姐时,他距图书馆的路程是米.23. 如图,四边形ABCD为矩形,AB=4cm,AD=3cm,点P从点A出发,以2cm/s的速度沿折线AD﹣DB向终点B运动,点Q从点B出发,以1cm/s的速度沿折线BC﹣CD向终点D运动.点P,Q两点同时出发,当一点到达终点时,另一点也随之停止,设运动的时间为ts,△PDQ的面积为Scm2(规定:线段是面积为0的特殊三角形)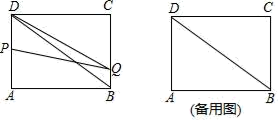 (1)、t的取值范围是.(2)、求S与t之间的函数关系式.(3)、连接AC,当PQ与△ABC的一条边平行(不包括重合)时,直接写出t的值.24. 定义:如果两个函数的图象关于原点O成中心对称,我们称这样的两个函数互为对称函数,由此定义可得一次函数的对称函数也是一次函数,二次函数的对称函数也是二次函数,反比例函数的对称函数是它本身.
(1)、t的取值范围是.(2)、求S与t之间的函数关系式.(3)、连接AC,当PQ与△ABC的一条边平行(不包括重合)时,直接写出t的值.24. 定义:如果两个函数的图象关于原点O成中心对称,我们称这样的两个函数互为对称函数,由此定义可得一次函数的对称函数也是一次函数,二次函数的对称函数也是二次函数,反比例函数的对称函数是它本身. (1)、若一个函数的图象过点(m,n),则这个函数的对称函数的图象一定过点.(2)、直接写出一次函数y=2x﹣4的对称函数的函数关系式.(3)、求二次函数y=x2﹣4x+t(t为常数)的对称函数的函数关系式.(4)、如图,若t≠0,且二次函数y=x2﹣4x+t的顶点为A,与y轴交点为B;二次函数y=x2﹣4x+t的对称函数的顶点为C,与y轴交点为D.连结AB,BC,CD,DA.
(1)、若一个函数的图象过点(m,n),则这个函数的对称函数的图象一定过点.(2)、直接写出一次函数y=2x﹣4的对称函数的函数关系式.(3)、求二次函数y=x2﹣4x+t(t为常数)的对称函数的函数关系式.(4)、如图,若t≠0,且二次函数y=x2﹣4x+t的顶点为A,与y轴交点为B;二次函数y=x2﹣4x+t的对称函数的顶点为C,与y轴交点为D.连结AB,BC,CD,DA.①当四边形ABCD为菱形时,此菱形的周长为.
②当四边形ABCD为矩形时,此矩形的面积为.