黑龙江省哈尔滨市阿城区2019届九年级调研测试数学试卷
试卷更新日期:2019-06-17 类型:中考模拟
一、单选题
-
1. |﹣5|的相反数是( )A、﹣5 B、5 C、 D、﹣2. 下列运算正确的是( )A、 B、 C、 D、3. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下图是由几个相同的小正方形搭成的一个几何体,它的俯视图是( )
4. 下图是由几个相同的小正方形搭成的一个几何体,它的俯视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 不等式组 的解集是( )A、 B、 C、 D、6. 抛物线 与 轴的交点坐标为( )A、 B、 C、 D、7. 若反比例函数 的图像经过点 ,则该函数图象位于( )A、第一、二象限 B、第二、四象限 C、第一、三象限 D、第三、四象限8. 如图,AB是⊙O的弦,半径OC⊥AB于点D,若⊙O的半径为5,AB=8,则CD的长是( )
5. 不等式组 的解集是( )A、 B、 C、 D、6. 抛物线 与 轴的交点坐标为( )A、 B、 C、 D、7. 若反比例函数 的图像经过点 ,则该函数图象位于( )A、第一、二象限 B、第二、四象限 C、第一、三象限 D、第三、四象限8. 如图,AB是⊙O的弦,半径OC⊥AB于点D,若⊙O的半径为5,AB=8,则CD的长是( )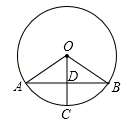 A、2 B、3 C、4 D、59. 如图,市政府准备修建一座高 为 的过街天桥,已知 为天桥的坡面 与底面 的夹角,且 ,则坡面 的长度为( )
A、2 B、3 C、4 D、59. 如图,市政府准备修建一座高 为 的过街天桥,已知 为天桥的坡面 与底面 的夹角,且 ,则坡面 的长度为( ) A、 B、 C、 D、10. 如图,点 是平行四边形 的边 上一点,射线 交 的延长线于点 ,则下列结论错误的是( )
A、 B、 C、 D、10. 如图,点 是平行四边形 的边 上一点,射线 交 的延长线于点 ,则下列结论错误的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
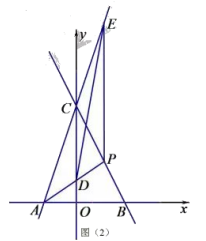
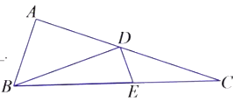
11. 截止2019年03月,全球 个国家人口总数为 人,其中中国以 人位居第一,成为世界上人口最多的国家,请将 用科学记数法表示为.12. 函数 中,自变量 的取值范围是.13. 计算: = .14. 因式分解: .15. 植树节这天有20名同学共种了52棵树苗,其中男生每人种树苗3棵,女生每人种树苗2棵,则男同学的人数为 人.16. 一个不透明的袋中,装有 个黄球、 个红球和 个白球,它们除颜色外都相同.从袋中任意摸出一个球,是白球的概率是.17. 一个扇形的面积是 ,圆心角是 ,则此扇形的半径是18. 已知抛物线 经过点 , ,则该抛物线的解析式为.19. 已知 ,点 在 上, ,点 在 上, ,则 的长是.20. 如图,在 中, ,点 分别在 边上, ,且 ,若 ,则 的长是.
三、解答题
-
21. 先化简,再求值: ,其中 .22. 如图 的网格中,每个小正方形的边长均为 ,线段 的端点都在小正方形的顶点上.(要求:下面所画图形的点 都在小正方形的顶点上)

 (1)、在图 中画一个以线段 为一边的等腰三角形 , ,使 的面积是 .(2)、在图 中画一个以线段 为一边的矩形 ,使矩形 的面积是 ,并直接写出矩形 的周长23. 在某区组织一次调研考试中,一道选择题(单选)有四个选项分别是 ,并且参加考试的每名学生都答出一个选项,在试卷分析时,将学生此题所答答案的“选项”进行了抽样调查.根据收集到的数据,绘制成如下两幅不完整的统计图,请根据图中提供的信息,完成下列问题:
(1)、在图 中画一个以线段 为一边的等腰三角形 , ,使 的面积是 .(2)、在图 中画一个以线段 为一边的矩形 ,使矩形 的面积是 ,并直接写出矩形 的周长23. 在某区组织一次调研考试中,一道选择题(单选)有四个选项分别是 ,并且参加考试的每名学生都答出一个选项,在试卷分析时,将学生此题所答答案的“选项”进行了抽样调查.根据收集到的数据,绘制成如下两幅不完整的统计图,请根据图中提供的信息,完成下列问题: (1)、这次抽样调查中共调查了多少人?(2)、求这次抽样调查中选择:“ 选项”和“ 选项”各多少人,并将条形统计图补充完整;(3)、若该区参加这次调研考试有 名学生,请估计选择“ 选项”的学生有多少人?24. 在菱形 中,点 是对角线的交点,点 是边 的中点,点 在 延长线上,且 .
(1)、这次抽样调查中共调查了多少人?(2)、求这次抽样调查中选择:“ 选项”和“ 选项”各多少人,并将条形统计图补充完整;(3)、若该区参加这次调研考试有 名学生,请估计选择“ 选项”的学生有多少人?24. 在菱形 中,点 是对角线的交点,点 是边 的中点,点 在 延长线上,且 .
 (1)、求证: ;(2)、如果 ,请写出图中所有的等边三角形.25. 某班级准备购买一些奖品奖励春季运动会表现突出的同学,奖品分为甲、乙两种,已知,购买一个甲奖品比一个乙奖品多用20元,若用400元购买甲奖品的个数是用160元购买乙奖品个数的一半.(1)、求购买一个甲奖品和一个乙奖品各需多少元?(2)、经商谈,商店决定给予该班级每购买甲奖品3个就赠送一个乙奖品的优惠,如果该班级需要乙奖品的个数是甲奖品的2倍还多8个,且该班级购买两种奖项的总费用不超过640元,那么该班级最多可购买多少个甲奖品?
(1)、求证: ;(2)、如果 ,请写出图中所有的等边三角形.25. 某班级准备购买一些奖品奖励春季运动会表现突出的同学,奖品分为甲、乙两种,已知,购买一个甲奖品比一个乙奖品多用20元,若用400元购买甲奖品的个数是用160元购买乙奖品个数的一半.(1)、求购买一个甲奖品和一个乙奖品各需多少元?(2)、经商谈,商店决定给予该班级每购买甲奖品3个就赠送一个乙奖品的优惠,如果该班级需要乙奖品的个数是甲奖品的2倍还多8个,且该班级购买两种奖项的总费用不超过640元,那么该班级最多可购买多少个甲奖品?