广西河池市2019届九年级数学中考模拟试卷(一)
试卷更新日期:2019-06-17 类型:中考模拟
一、单选题
-
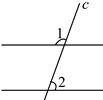
1. -2019的绝对值是( )A、 B、 C、2019 D、-20192. 如图,已知直线a∥b,直线c与a,b相交,∠1=110°,则∠2的度数为( )
 A、60° B、70° C、80° D、110°3. 下列计算正确的是( )A、 B、 C、 D、4. 如图是由三个小正方体叠成的一个几何体,它的左视图是( ).
A、60° B、70° C、80° D、110°3. 下列计算正确的是( )A、 B、 C、 D、4. 如图是由三个小正方体叠成的一个几何体,它的左视图是( ). A、
A、 B、
B、 C、
C、 D、
D、 5. 函数y= 中,自变量x的取值范围是( )A、x>1 B、x≥1 C、x<1 D、x≤16. 一个布袋里装有5个球,其中3个红球,2个白球,每个球除颜色外其他完全相同,从中任意摸出一个球,是红球的概率是( )A、 B、 C、 D、7. 一个不等式的解集为﹣1<x≤2,那么在数轴上表示正确的是( )A、
5. 函数y= 中,自变量x的取值范围是( )A、x>1 B、x≥1 C、x<1 D、x≤16. 一个布袋里装有5个球,其中3个红球,2个白球,每个球除颜色外其他完全相同,从中任意摸出一个球,是红球的概率是( )A、 B、 C、 D、7. 一个不等式的解集为﹣1<x≤2,那么在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 8. 一元二次方程 配方后化为( )A、 B、 C、 D、9. 将抛物线 向左平移2个单位后,得到的抛物线的解析式是( ).A、 B、 C、 D、10. 如图,在▱ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,若AB=6,EF=2,则BC的长为( )
8. 一元二次方程 配方后化为( )A、 B、 C、 D、9. 将抛物线 向左平移2个单位后,得到的抛物线的解析式是( ).A、 B、 C、 D、10. 如图,在▱ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,若AB=6,EF=2,则BC的长为( )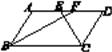 A、8 B、10 C、12 D、1411. 圆锥的母线长为4,底面半径为2,则此圆锥的侧面积是( )A、 B、 C、 D、12. 如图,RtΔABC中,AB=AC,D,E是斜边BC上两点,∠DAE=45°,将ΔADC绕点A顺时针旋转90°后,得到ΔAFB,连接EF,下列结论:①ΔAED≌ΔAEF,② ,③ΔABC的面积等于四边形AFBD的面积,④ ,⑤BE+DC=DE,其中正确的是( )
A、8 B、10 C、12 D、1411. 圆锥的母线长为4,底面半径为2,则此圆锥的侧面积是( )A、 B、 C、 D、12. 如图,RtΔABC中,AB=AC,D,E是斜边BC上两点,∠DAE=45°,将ΔADC绕点A顺时针旋转90°后,得到ΔAFB,连接EF,下列结论:①ΔAED≌ΔAEF,② ,③ΔABC的面积等于四边形AFBD的面积,④ ,⑤BE+DC=DE,其中正确的是( ) A、①②④ B、①③④ C、③④⑤ D、①③⑤
A、①②④ B、①③④ C、③④⑤ D、①③⑤二、填空题
-
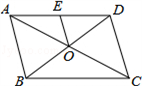
13. 计算: = .14. 方程 =1的解是.15. 一组数据3,4, ,5,8的平均数是6,则该组数据的中位数是.16. 已知直角三角形的两边长分别为3、4.则第三边长为.17. 如图,▱ABCD的对角线AC、BD交于点O,点E是AD的中点,△BCD的周长为18,则△DEO的周长是.
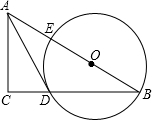
 18. 如图,直径为10的⊙A经过点C(0,6)和点O(0,0),与x轴的正半轴交于点D,B是y轴右侧圆弧上一点,则cos∠OBC的值为.
18. 如图,直径为10的⊙A经过点C(0,6)和点O(0,0),与x轴的正半轴交于点D,B是y轴右侧圆弧上一点,则cos∠OBC的值为.
三、解答题
-
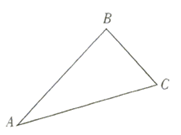
19. 计算: .20. 先化简,再求值: ,其中 .21. 如图,用尺规作图,并保留作图痕迹,ΔABC中,延长AC到E,使CE=CA,在线段AE与点B相异的一侧作∠CEM=∠A,延长BC交EM于点D,求证:ΔABC≌ΔEDC.
 22. “校园手机”现象越来越受到社会的关注.为了了解学生和家长对中学生带手机的态度,某记者随机调查了城区若干名学生和家长的看法,调查结果分为:赞成、无所谓、反对,并将调查结果绘制成如下不完整的统计表和统计图:
22. “校园手机”现象越来越受到社会的关注.为了了解学生和家长对中学生带手机的态度,某记者随机调查了城区若干名学生和家长的看法,调查结果分为:赞成、无所谓、反对,并将调查结果绘制成如下不完整的统计表和统计图: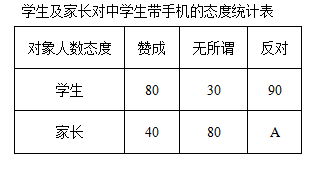

根据以上图表信息,解答下列问题:
(1)、统计表中的A ;(2)、统计图中表示家长“赞成”的圆心角的度数为度;(3)、从这次接受调查的学生中,随机抽查一个,恰好是持“反对”态度的学生的概率是多少?23. 某景点的门票价格如下边表格:某校七年级(1)、(2)两班共104人计划去游览该景点,其中(1)班人数少于50人,若两班都以班为单位单独购票,则一共支付1240元.购票人数/人
1~50
51~100
100以上
每人门票价/元
13
11
9
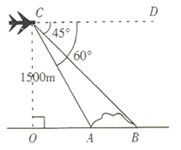
(1)、两个班各有多少名学生?(2)、如果两个班级联合起来,作为一个团体购票,可以省多少钱?(3)、如果七年级一班单独组织去博物馆参观,你认为如何购票最省钱?24. 如图,某高速公路建设中需要确定隧道 的长度.已知在离地面 高度 处的飞机上,测量人员测得正前方 、 两点处的俯角分别为 和 .求隧道 的长.(参考数据: )