广西贵港市港南区2019届九年级数学中考一模试卷

试卷更新日期：2019-06-17 类型：中考模拟

进入出卷网下载

一、单选题

1. -3的相反数是（）

A、3 B、-3 C、－ $\frac{1}{3}$ D、 $\frac{1}{3}$

查看试题解析
2. 下列计算正确的是（）

A、 $a + a = a^{2}$ B、 $6 a^{3} - 5 a^{2} = a$ C、 ${(2 x^{5})}^{2} = 4 x^{10}$ D、 $a^{6} \div a^{2} = a^{3}$

查看试题解析
3. 某市大力发展新能源汽车生产，预计2019年的产量达51.7万辆，将51.7万用科学记数法表示为（）

A、 $5.17 \times 10^{3}$ B、 $5.17 \times 10^{4}$ C、 $5.17 \times 10^{5}$ D、 $5.17 \times 10^{6}$

查看试题解析
4. 若一个正比例函数的图象经过A（3，﹣6），B（m，﹣4）两点，则m的值为（）

A、2 B、8 C、﹣2 D、﹣8

查看试题解析
5. 如果关于 $x$ 的方程 $(a - 5) x^{2} - 4 x - 1 = 0$ 有两个实数根，则 $a$ 满足的条件是（）

A、 $a \neq 5$ B、 $a \geq 1$ C、 $a > 1$ 且 $a \neq 5$ D、 $a \geq 1$ 且 $a \neq 5$

查看试题解析
6. 中国研究五谷丰登，六畜兴旺，如图是一个正方体展开图，图中的六个正方形内分别标有六畜：“猪”、“牛”、“羊”、“马”、“鸡”、“狗”将其围成一个正方体后，则与“牛”相对的是（）

A、羊 B、鸡 C、马 D、狗

查看试题解析
7. 下列说法正确的是（）

A、“经过有交通信号的路口，遇到红灯，” 是必然事件 B、已知某篮球运动员投篮投中的概率为 $0.6$ ，则他投 $10$ 次一定可投中 $6$ 次 C、处于中间位置的数一定是中位数 D、方差越大数据的波动越大，方差越小数据的波动越小

查看试题解析
8. 经过点 $(2 ， - 1)$ 一条直线与双曲线 $y = \frac{2}{x}$ 相交，当它们有且只有一个公共点时，这样的直线存在（）

A、2条 B、3条 C、4条 D、无数条

查看试题解析
9. 如图，四边形 $A O B C$ 和四边形 $C D E F$ 都是正方形，边 $O A$ 在 $x$ 轴上，边 $O B$ 在 $y$ 轴上，点 $D$ 在边 $C B$ 上，反比例函数 $y = \frac{8}{x}$ ，在第二象限的图像经过点 $E$ ，则正方形 $A O B C$ 与正方形 $C D E F$ 的面积之差为（）

A、6 B、8 C、10 D、12

查看试题解析
10. 如图， $A B ， A C$ 为 $⊙ O$ 的切线， $B$ 和 $C$ 是切点，延长 $O B$ 到点 $D$ ，使 $B D = O B$ ，连接 $A D$ ，若 $∠ D A C = 78^{\circ}$ ，则 $∠ A D O$ 等于（）

A、 $70^{\circ}$ B、 $64^{\circ}$ C、 $62^{\circ}$ D、 $51^{\circ}$

查看试题解析
11. 如图， $R t Δ A B C$ 中， $A B ⊥ B C ， A B = 6 ， B C = 4 ， P$ 是 $Δ A B C$ 内部的一个动点，且满足 $∠ P A B = ∠ P B C$ ，则线段 $C P$ 长的最小值为（）

A、 $\frac{4 \sqrt{13}}{13}$ B、 $\frac{8 \sqrt{13}}{13}$ C、 $2$ D、 $4$

查看试题解析
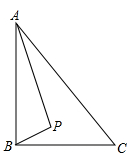12. 如图，在△ABC中，AD和BE是高，∠ABE=45°，点F是AB的中点，AD与FE、BE分别交于点G、H，∠CBE=∠BAD．有下列结论：①FD=FE；②AH=2CD；③BC•AD= $\sqrt{2}$ AE²；④∠DFE=2∠DAC；⑤若连接CH，则CH∥EF，其中正确的个数为（）

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

13. 因式分解： $9 y^{2} - 81 =$ .

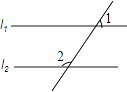
查看试题解析
14. 如图，l₁∥l₂ ， ∠1=56°，则∠2的度数为．

查看试题解析
15. 已知一组正数 $a_{1}, a_{2}, a_{3}, a_{4}$ 的平均数为 $2$ ，则 $a_{1} + 1, a_{2} + 2, a_{3} + 3, a_{4} + 4$ 的平均数为.

查看试题解析
16. 如图，已知⊙ $O$ 半径为 $2$ ，从⊙ $O$ 外点 $C$ 作⊙ $O$ 的切线 $C A$ 和 $C B$ ，切点分别为点 $A$ 和点 $D$ ， $∠ A C B = 90^{0} ， B C = 2 \sqrt{3}$ ，则图中阴影部分的面积是.

查看试题解析
17. 如图所示，已知：点 $A (0.0)$ ，点 $B (\sqrt{3} ， 0)$ ，点 $C (0 ， 1)$ ，在 $Δ A B C$ 内依次作等边三角形，使一边在 $x$ 轴上，另一个顶点在 $B C$ 边上，作出的等边三角形分别是第 $1$ 个 $Δ A A_{1} B_{1}$ ，第 $2$ 个 $Δ B_{1} A_{2} B_{2}$ ，第 $3$ 个 $Δ B_{2} A_{3} B_{3}$ ， $\dots$ ，则第 $n$ 个等边三角形的边长等于 .

查看试题解析

三、解答题

18.

(1)、计算： ${(- 1)}^{2019} - | \sqrt{3} - 2 | - {(π - 3.14)}^{0} + \sqrt{12} sin 60^{0}$

(2)、化简： $(\frac{m}{m - 2} - \frac{2 m}{m^{2} - 4}) \div \frac{m}{m + 2}$ ，请在 $2, - 2, 0, 3$ 中选一个合适的数代入求值.

查看试题解析
19. 如图，在 $R t Δ A B C$ 中， $∠ A C B = 90^{0}$ ，

(1)、请用直尺和圆规按下列步骤作图（保留作图痕迹），①作 $∠ A C B$ 的平分线，交斜边AB于点D；②过点D作AC的垂线，垂足为E.

(2)、在（1）作出的图形中，若 $C B = 4 ， C A = 6$ ，则DE= .

查看试题解析
20. 如图，直线 $y = k x + b (k \neq 0)$ 与双曲线 $y = \frac{2}{x}$ 相交于 $A (1 ， m) ， B (- 2. - 1)$ 两点，

(1)、求直线的解析式；

(2)、连接 $O A ， O B$ ，求 $Δ A O B$ 的面积.

查看试题解析
21. 为庆祝即将到来的“三月三”壮族传统节日，某校举行了书法比赛，赛后随机抽查部分参赛同学的成绩，并制作成如下图表：

请根据如上图表提供的信息，解答下列问题：

(1)、这次随机抽查了名学生，表中的数 $m =$ . $n =$ .

(2)、请在图中补全频数分布直方图；

(3)、若绘制扇形统计图，分数段 $60 \leq x < 70$ 所对应扇形的圆心角为度；

(4)、全校共有 $600$ 名学生参加比赛，估计该校成绩 $80 \leq x \leq 100$ 范围内的学生有多少人？

查看试题解析
22. 随着人民生活水平的不断提高，我市家庭轿车的拥有量逐年增加，据统计，某小区 $2016$ 年底拥有家庭轿车 $640$ 辆， $2018$ 年底家庭轿车的拥有量达到 $1000$ 辆.

(1)、若该小区 $2016$ 年底到 $2019$ 年底家庭轿车拥有量的年平均增长率都相同，求该小区到 $2019$ 年底家庭轿车将达到多少辆？

(2)、为了解决停车困难，该小区决定投资 $30$ 万元再建造若干个停车位，据测算，室内车位建造费用 $5000$ 元 $/$ 个，露天车位建造费用 $1000$ 元 $/$ 个，考虑到实际因素，计划露天车位的数量不少于室内车位的 $2$ 倍，但不超过室内车位的 $2.5$ 倍，求该小区建造车位共有几种方案？

查看试题解析
23. 如图，在 $Δ A C B$ 中， $∠ C = 90^{0} ， B C = \frac{1}{2} A B$ ，点 $O$ 在边 $A B$ 上，且 $A B = 3 O B$ ，以 $O$ 为圆心， $O B$ 长为半径的圆分别交 $A B$ ， $B C$ 于 $D ， E$ 两点.

(1)、求证： $A C$ 是⊙ $O$ 的切线；

(2)、判断由 $A C$ 与⊙ $O$ 的切点及点 $D ， O ， E$ 所构成的四边形的形状，并说明理由.

查看试题解析
24. 如图，抛物线 $y = x^{2} - 2 m x + 3 m$ 与x轴交于 $A ， B$ 两点，与 $y$ 轴交于点 $C (0 ， - 3)$ .

(1)、求该抛物线的解析式；

(2)、若点 $E$ 为线段 $O C$ 上一动点，试求 $A E + \frac{\sqrt{2}}{2} E C$ 的最小值；

(3)、点 $D$ 是 $y$ 轴左侧的抛物线上一动点，连接 $A C$ ，当 $∠ D A B = ∠ A C O$ 时，求点 $D$ 的坐标.

查看试题解析
25. 已知长方形 $A B C D$ 中， $A D = 10 c m ， A B = 6 c m$ ，点 $M$ 在边 $C D$ 上，由 $C$ 往 $D$ 运动，速度为 $1 c m / s$ ，运动时间为 $t$ 秒，将 $Δ A D M$ 沿着 $A M$ 翻折至 $Δ A D^{'} M$ ，点 $D$ 对应点为 $D^{'}$ ， $A D^{'}$ 所在直线与边 $B C$ 交与点 $P$ ，

(1)、如图 $1$ ，当 $t = 0$ 时，求证： $P A = P C$ ；

(2)、如图 $2$ ，当 $t$ 为何值时，点 $D^{'}$ 恰好落在边 $B C$ 上；

(3)、如图 $3$ ，当 $t = 3$ 时，求 $C P$ 的长.

查看试题解析