广西防城港市防城区2019届九年级中考数学二模试卷
试卷更新日期:2019-06-17 类型:中考模拟
一、单选题
-
1. 若实数a、b互为相反数,则下列等式中成立的是( )A、a﹣b=0 B、a+b=0 C、ab=1 D、ab=﹣12. 下列实数中,无理数是( )A、﹣1 B、 C、 D、3.3. 中国倡导的“一带一路”建设将促进我国与世界各国的互利合作,根据规划“一带一路”地区覆盖总人口44亿,这个数用科学记数法表示为( )A、44×108 B、4.4×109 C、4.4×108 D、4.4×10104. 计算(﹣x2)3的结果是( )A、﹣x6 B、x6 C、﹣x5 D、﹣x85. 一个多边形的内角和是720°,这个多边形的边数是( )A、6 B、7 C、8 D、96. 已知△ABC∽△DEF,面积比为9∶4,则△ABC与△DEF的对应边之比为( )A、3∶4 B、2∶3 C、9∶16 D、3∶27. 已知一组数据1,5,6,5,5,6,6,6,则下列说法正确的是( )A、众数是5 B、中位数是5 C、平均数是5 D、极差是48. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、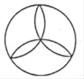 9. 从三个不同方向看一个几何体,得到的平面图形如图所示,则这个几何体是( )
9. 从三个不同方向看一个几何体,得到的平面图形如图所示,则这个几何体是( )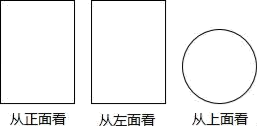 A、圆柱 B、圆锥 C、棱锥 D、球10. ∠BAC放在正方形网格纸的位置如图,则tan∠BAC的值为( )
A、圆柱 B、圆锥 C、棱锥 D、球10. ∠BAC放在正方形网格纸的位置如图,则tan∠BAC的值为( ) A、 B、 C、 D、11. 二次函数y=ax2+bx+c(a、b、c为常数且a≠0)中的x与y的部分对应值如下表,该抛物线的对称轴是直线( )
A、 B、 C、 D、11. 二次函数y=ax2+bx+c(a、b、c为常数且a≠0)中的x与y的部分对应值如下表,该抛物线的对称轴是直线( )x
﹣1
0
1
3
y
﹣1
3
5
3
A、x=0 B、x=1 C、x=1.5 D、x=212. 如图,有一电路AB是由图示的开关控制,闭合a,b,c,d,e五个开关中的任意两个开关,使电路形成通路,则使电路形成通路的概率是( )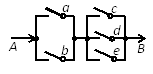 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 计算2 ﹣ =.14. 解分式方程: 得.15. 因式分解:a3-ab2=.16.
如图,在⊙O中,AB为直径,C、D为⊙O上两点,若∠C=25°,则∠ABD= .
 17. 如图,在平面直角坐标系中,已知点O(0,0),A(6,0),B(0,8),以某点为位似中心,作出△AOB的位似△CDE,则位似中心的坐标为.
17. 如图,在平面直角坐标系中,已知点O(0,0),A(6,0),B(0,8),以某点为位似中心,作出△AOB的位似△CDE,则位似中心的坐标为.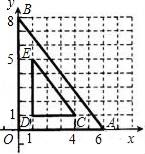 18. 如图,把△ABC沿EF翻折,叠合后的图形如图.若∠A=60°,∠1=95°,则∠2的度数为.
18. 如图,把△ABC沿EF翻折,叠合后的图形如图.若∠A=60°,∠1=95°,则∠2的度数为.
三、解答题
-
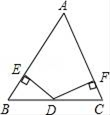
19. 计算(1)、 ;(2)、20. 解不等式组 .21. 如图,在△ABC中,AB=AC,D是底边BC的中点,作DE⊥AB于E,DF⊥AC于F
求证:DE=DF.
证明:∵AB=AC,∴∠B=∠C①.
在△BDE和△CDF中,∠B=∠C,∠BED=∠CFD,BD=CD,∴△BDE≌△CDF②.∴DE=DF③.
 (1)、上面的证明过程是否正确?若正确,请写出①、②和③的推理根据.(2)、请你写出另一种证明此题的方法.22. 某市为提高学生参与体育活动的积极性,围绕“你喜欢的体育运动项目(只写一项)”这一问题,对初一新生进行随机抽样调查.下面是根据调查结果绘制成的统计图(不完整).
(1)、上面的证明过程是否正确?若正确,请写出①、②和③的推理根据.(2)、请你写出另一种证明此题的方法.22. 某市为提高学生参与体育活动的积极性,围绕“你喜欢的体育运动项目(只写一项)”这一问题,对初一新生进行随机抽样调查.下面是根据调查结果绘制成的统计图(不完整).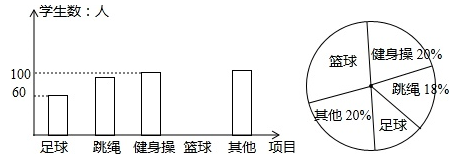
请你根据图中提供的信息解答下列问题:
(1)、本次抽样调查一共调查调查了多少名学生?(2)、根据条形统计图中的数据,求扇形统计图中“最喜欢足球运动”的学生数对应扇形的圆心角度数.(3)、请将条形图补充完整.(4)、若该市2017年约有初一新生21000人,请你估计全市本届学生中“最喜欢足球运动”的学生有多少人?23. 如图,在⊙O中,直径CD垂直于不过圆心O的弦AB,垂足为点N,连接AC,BC,点E在AB上,且AE=CE. (1)、求证:∠ABC=∠ACE;(2)、过点B作⊙O的切线交EC的延长线于点P,证明PB=PE;(3)、在第(2)问的基础上,设⊙O半径为2 ,若点N为OC中点,点Q在⊙O上,求线段PQ的最大值.24. 如图:是某出租车单程收费y(元)与行驶路程x(千米)之间的函数关系图象,根据图象回答下列问题:
(1)、求证:∠ABC=∠ACE;(2)、过点B作⊙O的切线交EC的延长线于点P,证明PB=PE;(3)、在第(2)问的基础上,设⊙O半径为2 ,若点N为OC中点,点Q在⊙O上,求线段PQ的最大值.24. 如图:是某出租车单程收费y(元)与行驶路程x(千米)之间的函数关系图象,根据图象回答下列问题: (1)、当行使8千米时,收费应为元;(2)、从图象上你能获得哪些信息?(请写出2条)
(1)、当行使8千米时,收费应为元;(2)、从图象上你能获得哪些信息?(请写出2条)①
②
(3)、求出收费y(元)与行使x(千米)(x≥3)之间的函数关系式.25. 如图1,在△OAB中,∠OAB=90°,∠AOB=30°,OB=8.以OB为边,在△OAB外作等边△OBC,D是OB的中点,连接AD并延长交OC于E.
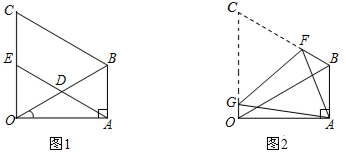 (1)、求证:四边形ABCE是平行四边形;(2)、如图2,将图1中的四边形ABCO折叠,使点C与点A重合,折痕为FG,求OG的长.26. 如图,在平面直角坐标系xOy中,已知正比例函数y1=﹣2x的图象与反比例函数y2= 的图象交于A(﹣1,n),B两点.
(1)、求证:四边形ABCE是平行四边形;(2)、如图2,将图1中的四边形ABCO折叠,使点C与点A重合,折痕为FG,求OG的长.26. 如图,在平面直角坐标系xOy中,已知正比例函数y1=﹣2x的图象与反比例函数y2= 的图象交于A(﹣1,n),B两点. (1)、求出反比例函数的解析式及点B的坐标;(2)、观察图象,请直接写出满足 y2 ≤2的取值范围
(1)、求出反比例函数的解析式及点B的坐标;(2)、观察图象,请直接写出满足 y2 ≤2的取值范围
(3)、点P是第四象限内反比例函数的图象上一点,若△POB的面积为1,请直接写出点P的横坐标.