广东省茂名市茂南区2019年数学中考一模试卷
试卷更新日期：2019-06-17 类型：中考模拟
一、单选题
-
1. 的倒数是（ ）A、 B、 C、 D、2. 我县人口约为530060人，用科学记数法可表示为（ ）A、53006×10人 B、5.3006×105人 C、53×104人 D、0.53×106人3. 如图，BC为⊙O直径，交弦AD于点E，若B点为弧AD中点，则说法错误的是（ ）
A、AD⊥BC B、弧AC=弧CD C、AE＝DE D、OE＝BE4. 由方程组 可得出x与y之间的关系是（ ）．A、x＋y＝1 B、x＋y＝－1 C、x＋y＝7 D、x＋y＝－75. 如图是一个正方体的平面展开图，正方体中相对的面上的数字或代数式互为相反数，则2x+y的值为（ ）
A、0 B、﹣1 C、﹣2 D、16. 从一个多边形的任何一个顶点出发都只有5条对角线，则它的边数是（ ）A、6 B、7 C、8 D、97. 下列调查方式，你认为最合适的是（ ）A、了解北京市每天的流动人口数，采用抽样调查方式 B、旅客上飞机前的安检，采用抽样调查方式 C、了解北京市居民”一带一路”期间的出行方式，采用全面调查方式 D、日光灯管厂要检测一批灯管的使用寿命，采用全面调查方式8. 某区“引进人才”招聘考试分笔试和面试．其中笔试按60%、面试按40%计算加权平均数作为总成绩．吴老师笔试成绩为90分．面试成绩为85分，那么吴老师的总成绩为（ ）分．A、85 B、86 C、87 D、889. 在﹣3，1，0，﹣1这四个数中，最大的数是（ ）A、﹣3 B、﹣1 C、0 D、110. 如图，在△ABC中，E，F分别是AB，AC的中点.若△ABC的面积是8，则四边形BCEF的面积是（ ）
A、4 B、5 C、6 D、7二、填空题
-
11. 因式分解：9a3b﹣ab＝.12. 空调安装在墙上时，一般都会采用如图所示的方法固定，这种方法应用的几何原理是.
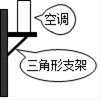13. 当x =时，分式 值为0.14. 已知每个网格中小正方形的边长都是1，如图中的阴影图案是由三段以格点为圆心，半径分别为1和2的圆弧围成.则阴影部分的面积是.
15. 如图，已知直线y= 与x轴、y轴分别交于A、B两点，P是以C（0，1）为圆心，1为半径的圆上一动点，连结PA、PB.则△PAB面积的最小值是.
三、解答题
-
16. 化简：x(4x＋3y)－(2x＋y)(2x－y)17. 若关于x的不等式组 恰有三个整数解，求实数a的取值范围。18. 如图，适当地改变方格图中的平行四边形的部分位置，并保持面积不变，先使其为矩形，再将矩形向下平移3个格后，继续改变其中某些部分的位置并保持面积不变，使其成为菱形.说明在变化过程中所运用的图形变换.
19. 为了满足广大手机用户的需求，某移动通信公司推出了三种套餐，资费标准如下表所示：套餐资费标准
月套餐类型
套餐费用
套餐包含内容
超出套餐后的费用
本地主叫市话
短信
国内移动数据流量
本地主叫市话
短信
国内移动数据流量
套餐一
18元
30分钟
100条
50兆
0.1元/
分钟
0.1元/条
0.5元/兆
套餐二
28元
50分钟
150条
100兆
套餐三
38元
80分钟
200条
200兆
小莹选择了该移动公司的一种套餐，下面两个统计图都反映了她的手机消费情况.
(1)、已知小莹2013年10月套餐外通话费为33.6元，则她选择的上网套餐为套餐（填“一”、“二”或“三”）；(2)、补全条形统计图，并在图中标明相应的数据；(3)、根据2013年后半年每月的消费情况，小莹估计自己每月本地主叫市话通话大约430分钟，发短信大约240条，国内移动数据流量使用量大约为120兆，除此之外不再产生其他费用，则小莹应该选择套餐最划算（填“一”、“二”或“三”）；选择该套餐后，她每月的手机消费总额约为元.20. 如图，在矩形ABCD中，E是BC上一点，且AE＝BC，DF⊥AE，垂足是F，连接DE.
求证：
(1)、DF＝AB；(2)、DE是∠FDC的平分线.21. 某企业设计了一款工艺品，每件的成本是50元，为了合理定价，投放市场进行试销．据市场调查，销售单价是100元时，每天的销售量是50件，而销售单价每降低1元，每天就可多售出5件，但要求销售单价不得低于成本．(1)、求出每天的销售利润y（元）与销售单价x（元）之间的函数关系式；(2)、求出销售单价为多少元时，每天的销售利润最大？最大利润是多少？(3)、如果该企业要使每天的销售利润不低于4000元，那么销售单价应控制在什么范围内？
