广东省广州市天河区2019届九年级中考数学一模试卷
试卷更新日期:2019-06-17 类型:中考模拟
一、单选题
-
1. 9的平方根是( )A、 ±3 B、﹣3 C、3 D、2. 下列各式计算正确的是( )A、3a3+2a2=5a6 B、 C、a4•a2=a8 D、(ab2)3=ab63.
已知两个不等式的解集在数轴上如右图表示,那么这个解集为( )
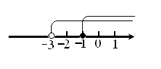 A、x≥-1 B、x>1 C、-3<x≤-1 D、x>-34. 如图,AB∥CD,DE⊥BE,BF、DF分别为∠ABE、∠CDE的角平分线,则∠BFD=( )
A、x≥-1 B、x>1 C、-3<x≤-1 D、x>-34. 如图,AB∥CD,DE⊥BE,BF、DF分别为∠ABE、∠CDE的角平分线,则∠BFD=( )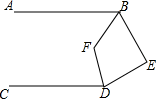 A、110° B、120° C、125° D、135°5. 如图是由几个相同的正方体搭成的一个几何体,从正面看到的平面图形是( )
A、110° B、120° C、125° D、135°5. 如图是由几个相同的正方体搭成的一个几何体,从正面看到的平面图形是( )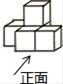 A、
A、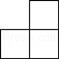 B、
B、 C、
C、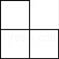 D、
D、 6. 某篮球运动员在连续7场比赛中的得分(单位:分)依次为20,18,23,17,20,20,18,则这组数据的众数与中位数分别是( )A、18分,17分 B、20分,17分 C、20分,19分 D、20分,20分7. 要组织一次篮球比赛,赛制为主客场形式(每两队之间都需在主客场各赛一场),计划安排30场比赛,设邀请x个球队参加比赛,根据题意可列方程为( )A、x(x﹣1)=30 B、x(x+1)=30 C、 =30 D、 =308. 如图,从热气球C处测得地面A,B两点的俯角分别是30°、45°,如果此时热气球C处的高度CD为100米,点A,D,B在同一直线上,则AB两点的距离是( )
6. 某篮球运动员在连续7场比赛中的得分(单位:分)依次为20,18,23,17,20,20,18,则这组数据的众数与中位数分别是( )A、18分,17分 B、20分,17分 C、20分,19分 D、20分,20分7. 要组织一次篮球比赛,赛制为主客场形式(每两队之间都需在主客场各赛一场),计划安排30场比赛,设邀请x个球队参加比赛,根据题意可列方程为( )A、x(x﹣1)=30 B、x(x+1)=30 C、 =30 D、 =308. 如图,从热气球C处测得地面A,B两点的俯角分别是30°、45°,如果此时热气球C处的高度CD为100米,点A,D,B在同一直线上,则AB两点的距离是( )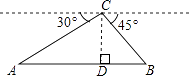 A、200米 B、200 米 C、220 米 D、100( )米9. 如图,在平面直角坐标系中,OABC是正方形,点A的坐标是(4,0),点P为边AB上一点,∠CPB=60°,沿CP折叠正方形,折叠后,点B落在平面内点B′处,则B′点的坐标为( )
A、200米 B、200 米 C、220 米 D、100( )米9. 如图,在平面直角坐标系中,OABC是正方形,点A的坐标是(4,0),点P为边AB上一点,∠CPB=60°,沿CP折叠正方形,折叠后,点B落在平面内点B′处,则B′点的坐标为( )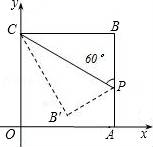 A、(2,2 ) B、( , ) C、(2, ) D、( , )10. 如图,△ABC是等腰直角三角形,AC=BC=a,以斜边AB上的点O为圆心的圆分别与AC,BC相切于点E、F,与AB分别相交于点G、H,且EH的延长线与CB的延长线交于点D,则CD的长为( )
A、(2,2 ) B、( , ) C、(2, ) D、( , )10. 如图,△ABC是等腰直角三角形,AC=BC=a,以斜边AB上的点O为圆心的圆分别与AC,BC相切于点E、F,与AB分别相交于点G、H,且EH的延长线与CB的延长线交于点D,则CD的长为( )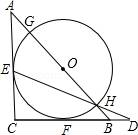 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
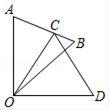
11. ﹣1 的绝对值是 , 倒数是.12. 若代数式 有意义,则m的取值范围是.13. 如图,△COD是△AOB绕点O顺时针方向旋转40°后所得的图形,点C恰好在AB上,则∠A的度数是.
 14. 关于x的一元二次方程(m﹣3)x2+x+(m2﹣9)=0的一个根是0,则m的值是 .15. 已知⊙O的半径为5cm,弦AB∥CD,AB=8cm,CD=6cm,则AB和CD的距离为.16. 如图,在平面直角坐标中,直线l经过原点,且与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线l于点B,过点B1作作直线l的垂线交y轴于点A1 , 以A1B.BA为邻边作 ABA1C1;过点A1作y轴的垂线交直线l于点B1 , 过点B1作直线l的垂线交y轴于点A2 , 以A2B1.B1A1为邻边作 A1B1A2C2;…;按此作法继续下去,则Cn的坐标是
14. 关于x的一元二次方程(m﹣3)x2+x+(m2﹣9)=0的一个根是0,则m的值是 .15. 已知⊙O的半径为5cm,弦AB∥CD,AB=8cm,CD=6cm,则AB和CD的距离为.16. 如图,在平面直角坐标中,直线l经过原点,且与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线l于点B,过点B1作作直线l的垂线交y轴于点A1 , 以A1B.BA为邻边作 ABA1C1;过点A1作y轴的垂线交直线l于点B1 , 过点B1作直线l的垂线交y轴于点A2 , 以A2B1.B1A1为邻边作 A1B1A2C2;…;按此作法继续下去,则Cn的坐标是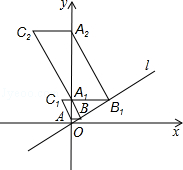 17. 如图:AD是正△ABC的高,O是AD上一点,⊙O经过点D,分别交AB、AC于E、F.
17. 如图:AD是正△ABC的高,O是AD上一点,⊙O经过点D,分别交AB、AC于E、F.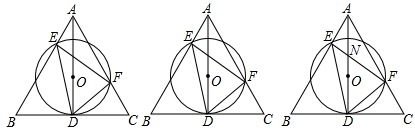 (1)、求∠EDF的度数;(2)、若AD= ,求△AEF的周长;(3)、设EF、AD相较于N,若AE=3,EF=7,求DN的长.
(1)、求∠EDF的度数;(2)、若AD= ,求△AEF的周长;(3)、设EF、AD相较于N,若AE=3,EF=7,求DN的长.三、解答题
-
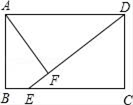
18. 解方程组(1)、 ;(2)、 .19. 已知:如图,矩形ABCD中,DE交BC于E,且DE=AD,AF⊥DE于F.
求证:AB=AF.
 20. 如图,在平面直角坐标系中有△ABC,其中A(﹣3,4),B(﹣4,2),C(﹣2,1).把△ABC绕原点顺时针旋转90°,得到△A1B1C1.再把△A1B1C1向左平移2个单位,向下平移5个单位得到△A2B2C2.
20. 如图,在平面直角坐标系中有△ABC,其中A(﹣3,4),B(﹣4,2),C(﹣2,1).把△ABC绕原点顺时针旋转90°,得到△A1B1C1.再把△A1B1C1向左平移2个单位,向下平移5个单位得到△A2B2C2. (1)、画出△A1B1C1和△A2B2C2.(2)、直接写出点B1、B2坐标.(3)、P(a,b)是△ABC的AC边上任意一点,△ABC经旋转平移后P对应的点分别为P1、P2 , 请直接写出点P1、P2的坐标.21. 已知一个不透明的袋子中装有7个只有颜色不同的球,其中2个白球,5个红球.(1)、求从袋中随机摸出一个球是红球的概率.(2)、从袋中随机摸出一个球,记录颜色后放回,摇匀,再随机摸出一个球,求两次摸出的球恰好颜色不同的概率.(3)、若从袋中取出若干个红球,换成相同数量的黄球.搅拌均匀后,使得随机从袋中摸出两个球,颜色是一白一黄的概率为 ,求袋中有几个红球被换成了黄球.22. 2018年我市的脐橙喜获丰收,脐橙一上市,水果店的陈老板用2400元购进一批脐橙,很快售完;陈老板又用6000元购进第二批脐橙,所购件数是第一批的2倍,但进价比第一批每件多了20元.(1)、第一批脐橙每件进价多少元?(2)、陈老板以每件120元的价格销售第二批脐橙,售出 后,为了尽快售完,决定打折促销,要使第二批脐橙的销售总利润不少于480元,剩余的脐橙每件售价最低打几折?(利润=售价-进价)23. 如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC边于点D,E是边BC的中点,连接DE、OD,
(1)、画出△A1B1C1和△A2B2C2.(2)、直接写出点B1、B2坐标.(3)、P(a,b)是△ABC的AC边上任意一点,△ABC经旋转平移后P对应的点分别为P1、P2 , 请直接写出点P1、P2的坐标.21. 已知一个不透明的袋子中装有7个只有颜色不同的球,其中2个白球,5个红球.(1)、求从袋中随机摸出一个球是红球的概率.(2)、从袋中随机摸出一个球,记录颜色后放回,摇匀,再随机摸出一个球,求两次摸出的球恰好颜色不同的概率.(3)、若从袋中取出若干个红球,换成相同数量的黄球.搅拌均匀后,使得随机从袋中摸出两个球,颜色是一白一黄的概率为 ,求袋中有几个红球被换成了黄球.22. 2018年我市的脐橙喜获丰收,脐橙一上市,水果店的陈老板用2400元购进一批脐橙,很快售完;陈老板又用6000元购进第二批脐橙,所购件数是第一批的2倍,但进价比第一批每件多了20元.(1)、第一批脐橙每件进价多少元?(2)、陈老板以每件120元的价格销售第二批脐橙,售出 后,为了尽快售完,决定打折促销,要使第二批脐橙的销售总利润不少于480元,剩余的脐橙每件售价最低打几折?(利润=售价-进价)23. 如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC边于点D,E是边BC的中点,连接DE、OD,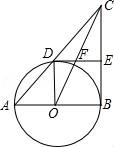 (1)、求证:直线DE是⊙O的切线;(2)、连接OC交DE于F,若OF=FC,试判断△ABC的形状,并说明理由;(3)、若 ,求⊙O的半径.24. 已知反比例函数y= 的图象的一支位于第一象限,点A(x1 , y1),B(x2 , y2)都在该函数的图象上.
(1)、求证:直线DE是⊙O的切线;(2)、连接OC交DE于F,若OF=FC,试判断△ABC的形状,并说明理由;(3)、若 ,求⊙O的半径.24. 已知反比例函数y= 的图象的一支位于第一象限,点A(x1 , y1),B(x2 , y2)都在该函数的图象上.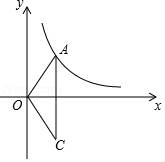 (1)、m的取值范围是 , 函数图象的另一支位于第一象限,若x1>x2 , y1>y2 , 则点B在第象限;(2)、如图,O为坐标原点,点A在该反比例函数位于第一象限的图象上,点C与点A关于x轴对称,若△OAC的面积为6,求m的值.25. 如图1,抛物线y=ax2+bx+3交x轴于点A(﹣1,0)和点B(3,0).
(1)、m的取值范围是 , 函数图象的另一支位于第一象限,若x1>x2 , y1>y2 , 则点B在第象限;(2)、如图,O为坐标原点,点A在该反比例函数位于第一象限的图象上,点C与点A关于x轴对称,若△OAC的面积为6,求m的值.25. 如图1,抛物线y=ax2+bx+3交x轴于点A(﹣1,0)和点B(3,0).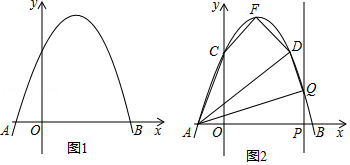 (1)、求该抛物线所对应的函数解析式;(2)、如图2,该抛物线与y轴交于点C,顶点为F,点D(2,3)在该抛物线上.
(1)、求该抛物线所对应的函数解析式;(2)、如图2,该抛物线与y轴交于点C,顶点为F,点D(2,3)在该抛物线上.①求四边形ACFD的面积;
②点P是线段AB上的动点(点P不与点A、B重合),过点P作PQ⊥x轴交该抛物线于点Q,连接AQ、DQ,当△AQD是直角三角形时,求出所有满足条件的点Q的坐标.