广东省广州市海珠区2019届九年级中考数学一模试卷
试卷更新日期:2019-06-17 类型:中考模拟
一、单选题
-
1. 若a2=4,b2=9,且ab<0,则a﹣b的值为( )A、﹣2 B、±5 C、5 D、﹣52. 下列计算正确的是( )A、x2•x3=x6 B、(x2)3=x5 C、 D、x5﹣x2=x33. 一元一次不等式组 的解集在数轴上表示正确的是( )A、
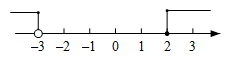
B、
B、 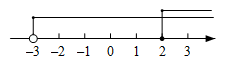
C、
C、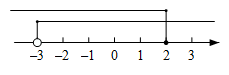
D、
D、
4. 如图,直线a∥b,AC⊥AB,AC交直线b于点C,∠1=55°,则∠2的度数是( )
4. 如图,直线a∥b,AC⊥AB,AC交直线b于点C,∠1=55°,则∠2的度数是( ) A、35° B、25° C、65° D、50°5. 如图,由5个完全相同的小正方体组合成一个立体图形,它的左视图是( )
A、35° B、25° C、65° D、50°5. 如图,由5个完全相同的小正方体组合成一个立体图形,它的左视图是( )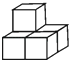 A、
A、 B、
B、 C、
C、 D、
D、 6. 某车间20名工人每天加工零件数如表所示:
6. 某车间20名工人每天加工零件数如表所示:每天加工零件数
4
5
6
7
8
人数
3
6
5
4
2
这些工人每天加工零件数的众数、中位数分别是( )
A、5,5 B、5,6 C、6,6 D、6,57. “凤鸣”文学社在学校举行的图书共享仪式上互赠图书,每个同学都把自己的图书向本组其他成员赠送一本,某组共互赠了210本图书,如果设该组共有x名同学,那么依题意,可列出的方程是( )A、x(x+1)=210 B、x(x﹣1)=210 C、2x(x﹣1)=210 D、 x(x﹣1)=2108. 某测量队在山脚A处测得山上树顶仰角为45°(如图),测量队在山坡上前进600米到D处,再测得树顶的仰角为60°,已知这段山坡的坡角为30°,如果树高为15米,则山高为( )(精确到1米, =1.732). A、585米 B、1014米 C、805米 D、820米9. 如图,在直角坐标系中,四边形OABC为正方形,顶点A,C在坐标轴上,以边AB为弦的⊙M与x轴相切,若点A的坐标为(0,8),则圆心M的坐标为( )
A、585米 B、1014米 C、805米 D、820米9. 如图,在直角坐标系中,四边形OABC为正方形,顶点A,C在坐标轴上,以边AB为弦的⊙M与x轴相切,若点A的坐标为(0,8),则圆心M的坐标为( ) A、(4,5) B、(﹣5,4) C、(﹣4,6) D、(﹣4,5)10. 如图,以正方形ABCD的AB边为直径作半圆O,过点C作直线切半圆于点E,交AD边于点F,则sin∠FCD=( )
A、(4,5) B、(﹣5,4) C、(﹣4,6) D、(﹣4,5)10. 如图,以正方形ABCD的AB边为直径作半圆O,过点C作直线切半圆于点E,交AD边于点F,则sin∠FCD=( )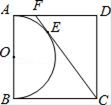 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 的绝对值是 , 倒数是.12. 要使代数式 有意义,x的取值范围是 .13. 如图,点 A、B、C、D 都在方格纸的格点上,若△AOB 绕点 O 按逆时针方向旋转到△COD 的位置,则旋转角为.
 14. 若a是方程 的解,计算: =.15. 已知⊙O的半径为26cm,弦AB∥CD,AB=48cm,CD=20cm,则AB、CD之间的距离为.16. 在直角坐标系内,设A(0,0),B(4,0),C(t+4,4),D(t,4)(t为实数),记N为平行四边形ABCD内部(不含边界)的整点的个数,其中整点是指横、纵坐标都是整数的点,则N的值可能为.
14. 若a是方程 的解,计算: =.15. 已知⊙O的半径为26cm,弦AB∥CD,AB=48cm,CD=20cm,则AB、CD之间的距离为.16. 在直角坐标系内,设A(0,0),B(4,0),C(t+4,4),D(t,4)(t为实数),记N为平行四边形ABCD内部(不含边界)的整点的个数,其中整点是指横、纵坐标都是整数的点,则N的值可能为.
三、解答题
-
17. 解方程组: .18. 如图,在矩形ABCD中,点E在BC上,AE=AD,DF⊥AE于F,连接DE.证明:DF=DC.
 19. 如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣4,2)、B(0,4)、C(0,2),
19. 如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣4,2)、B(0,4)、C(0,2), (1)、画出△ABC关于点C成中心对称的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;
(1)、画出△ABC关于点C成中心对称的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;
(2)、△A1B1C和△A2B2C2关于某一点成中心对称,则对称中心的坐标为 .
20. 某工厂准备购买A、B两种零件,已知A种零件的单价比B种零件的单价多30元,而用900元购买A种零件的数量和用600元购买B种零件的数量相等.(1)、求A、B两种零件的单价;(2)、根据需要,工厂准备购买A、B两种零件共200件,工厂购买两种零件的总费用不超过14700元,求工厂最多购买A种零件多少件?21. 如图,AB是⊙O的直径,点D在⊙O上,OC∥AD交⊙O于E, 点F在CD延长线上, 且∠BOC+∠ADF=90°. (1)、求证: ;(2)、求证:CD是⊙O的切线.22. 如图,已知点A在反比函数y= (k<0)的图象上,点B在直线y=x﹣3的图象上,点B的纵坐标为﹣1,AB⊥x轴,且S△OAB=4.
(1)、求证: ;(2)、求证:CD是⊙O的切线.22. 如图,已知点A在反比函数y= (k<0)的图象上,点B在直线y=x﹣3的图象上,点B的纵坐标为﹣1,AB⊥x轴,且S△OAB=4. (1)、求点A的坐标和k的值;(2)、若点P在反比例函数y= (k<0)的图象上,点Q在直线y=x﹣3的图象上,P、Q两点关于y轴对称,设点P的坐标为(m,n),求 + 的值.23. 已知,AB是⊙O的直径,点C在⊙O上,点P是AB延长线上一点,连接CP.
(1)、求点A的坐标和k的值;(2)、若点P在反比例函数y= (k<0)的图象上,点Q在直线y=x﹣3的图象上,P、Q两点关于y轴对称,设点P的坐标为(m,n),求 + 的值.23. 已知,AB是⊙O的直径,点C在⊙O上,点P是AB延长线上一点,连接CP. (1)、如图1,若∠PCB=∠A.
(1)、如图1,若∠PCB=∠A.①求证:直线PC是⊙O的切线;
②若CP=CA,OA=2,求CP的长;
(2)、如图2,若点M是弧AB的中点,CM交AB于点N,MN•MC=9,求BM的值.24. 已知,抛物线y=ax2+ax+b(a≠0)与直线y=2x+m有一个公共点M(1,0),且a<b. (1)、求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示);(2)、直线与抛物线的另外一个交点记为N,求△DMN的面积与a的关系式;(3)、a=﹣1时,直线y=﹣2x与抛物线在第二象限交于点G,点G、H关于原点对称,现将线段GH沿y轴向上平移t个单位(t>0),若线段GH与抛物线有两个不同的公共点,试求t的取值范围.
(1)、求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示);(2)、直线与抛物线的另外一个交点记为N,求△DMN的面积与a的关系式;(3)、a=﹣1时,直线y=﹣2x与抛物线在第二象限交于点G,点G、H关于原点对称,现将线段GH沿y轴向上平移t个单位(t>0),若线段GH与抛物线有两个不同的公共点,试求t的取值范围.