黑龙江省哈尔滨市建华区2019年数学中考模拟试卷(4月)
试卷更新日期:2019-06-17 类型:中考模拟
一、单选题
-
1. 若x与3互为相反数,则|x|+3等于( )A、﹣3 B、0 C、3 D、62. 下列运算正确的是( )A、a(a+1)=a2+1 B、(a2)3=a5 C、3a2+a=4a3 D、a5÷a2=a33. 下列图形中,是轴对称图形但不是中心对称图形的是( )A、等边三角形 B、正六边形 C、正方形 D、圆4. 反比例函数 ,当 时, 随 的增大而减小,那么 的取值范围是( )A、 B、 C、 D、5. 如图是由几个相同的正方体搭成的一个几何体,从正面看到的平面图形是( )
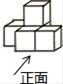 A、
A、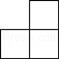 B、
B、 C、
C、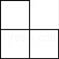 D、
D、 6. 如图,为了加快开凿隧道的施工进度,要在小山的两端同时施工.在 上找一点 ,取 ,要使 成一直线,那么开挖点 离点 的距离是( )
6. 如图,为了加快开凿隧道的施工进度,要在小山的两端同时施工.在 上找一点 ,取 ,要使 成一直线,那么开挖点 离点 的距离是( )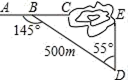 A、 B、 C、 D、7. 某地区2017年投入教育经费2500万元,预计到2019年共投入8000万元.设这两年投入教育经费的年平均增长率为x,则下列方程正确的是( )A、2500+2500(1+x)+2500(1+x)2=8000 B、2500x2=8000 C、2500(1+x)2=8000 D、2500(1+x)+2500(1+x)2=80008. 如图l1∥l2∥l3 , 若 ,DF=10,则DE=( )
A、 B、 C、 D、7. 某地区2017年投入教育经费2500万元,预计到2019年共投入8000万元.设这两年投入教育经费的年平均增长率为x,则下列方程正确的是( )A、2500+2500(1+x)+2500(1+x)2=8000 B、2500x2=8000 C、2500(1+x)2=8000 D、2500(1+x)+2500(1+x)2=80008. 如图l1∥l2∥l3 , 若 ,DF=10,则DE=( ) A、4 B、6 C、8 D、99. 如图,在 中, .点 是 的中点,连结 ,过点 作 ,分别交 于点 ,与过点 且垂直于 的直线相交于点 ,连结 .给出以下四个结论:① ;②点 是 的中点;③ ;④ ,其中正确的个数是( )
A、4 B、6 C、8 D、99. 如图,在 中, .点 是 的中点,连结 ,过点 作 ,分别交 于点 ,与过点 且垂直于 的直线相交于点 ,连结 .给出以下四个结论:① ;②点 是 的中点;③ ;④ ,其中正确的个数是( ) A、4 B、3 C、2 D、110. 如图,在 中, ,在同一平面内,将 绕点 旋转到 的位置,使得 ,则 。
A、4 B、3 C、2 D、110. 如图,在 中, ,在同一平面内,将 绕点 旋转到 的位置,使得 ,则 。
A. B. C. D.
二、填空题
-
11. 日地最近距离:147 100 000千米,用科学记数法表示为 .12. 二次根式 中,x的取值范围是.13. 计算2 ﹣ =.14. 因式分解:x3y2﹣x3=.15. 一个扇形的弧长是 ,它的面积是 ,这个扇形的圆心角度数是 .16. 不等式组 的解集是 .17. 已知关于x的二次函数y=ax2+(a2﹣1)x﹣a的图象与x轴的一个交点坐标为(m,0).若﹣4<m<﹣3,则a的取值范围是.18. 从1、2、3中任取一个数作为十位上的数字,再从余下的数字中任取一个数作为个位上的数字,那么组成的两位数是4的倍数的概率是19. Rt△ABC中,∠C=90°,cosA= ,AC=6cm,那么BC等于.20. 如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点F在边AC上,并且CF=1,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是.

三、解答题
-
21. 先化简,再求代数式 ÷(x﹣3﹣ )的值,其中x=3tan45°+2cos30°.22. 如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点。(1)、在图1中以格点为顶点画一个面积为5的正方形;
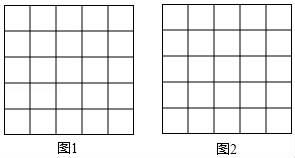 (2)、在图2中以格点为顶点画一个三角形,使三角形三边长分别为2, ,23. 某学校在倡导学生大课间活动中,随机抽取了部分学生对“我最喜爱课间活动”进行了一次抽样调查,分别从打篮球、踢足球、自由活动、跳绳、其它、等5个方面进行问卷调查(每人只能选一项),根据调查结果绘制了如图的不完整统计图,请你根据图中信息,解答下列问题
(2)、在图2中以格点为顶点画一个三角形,使三角形三边长分别为2, ,23. 某学校在倡导学生大课间活动中,随机抽取了部分学生对“我最喜爱课间活动”进行了一次抽样调查,分别从打篮球、踢足球、自由活动、跳绳、其它、等5个方面进行问卷调查(每人只能选一项),根据调查结果绘制了如图的不完整统计图,请你根据图中信息,解答下列问题 (1)、本次调查共抽取了学生多少人?(2)、求本次调查中喜欢踢足球人数,并补全条形统计图;(3)、若全校共有中学生1200人,请你估计我校喜欢跳绳学生有多少人.24. △ABC为等边三角形, . .
(1)、本次调查共抽取了学生多少人?(2)、求本次调查中喜欢踢足球人数,并补全条形统计图;(3)、若全校共有中学生1200人,请你估计我校喜欢跳绳学生有多少人.24. △ABC为等边三角形, . . (1)、求证:四边形 是菱形.(2)、若 是 的角平分线,连接 ,找出图中所有的等腰三角形.25. 某学校准备购买若干台电脑和打印机,如果购买1台电脑和2台打印机,一共花费5900元;如果购买2台电脑和1台打印机,一共花费8200元;(1)、求每台电脑和每台打印机的价格分别是多少元?(2)、如果学校购买电脑和打印机的预算费用不超过67000元,并且购买打印机的台数要比购买电脑的台数多1台,那么该学校最多能购买多少台打印机?26. 如图,AB为⊙O的直径,P是BA延长线上一点,CG是⊙O的弦∠PCA=∠ABC,CG⊥AB,垂足为D
(1)、求证:四边形 是菱形.(2)、若 是 的角平分线,连接 ,找出图中所有的等腰三角形.25. 某学校准备购买若干台电脑和打印机,如果购买1台电脑和2台打印机,一共花费5900元;如果购买2台电脑和1台打印机,一共花费8200元;(1)、求每台电脑和每台打印机的价格分别是多少元?(2)、如果学校购买电脑和打印机的预算费用不超过67000元,并且购买打印机的台数要比购买电脑的台数多1台,那么该学校最多能购买多少台打印机?26. 如图,AB为⊙O的直径,P是BA延长线上一点,CG是⊙O的弦∠PCA=∠ABC,CG⊥AB,垂足为D (1)、求证:PC是⊙O的切线;(2)、求证: ;(3)、过点A作AE∥PC交⊙O于点E,交CD于点F,连接BE,若sin∠P= ,CF=5,求BE的长.27. 抛物线y=﹣x2+bx+c经过点A、B、C,已知A(﹣1,0),C(0,3).
(1)、求证:PC是⊙O的切线;(2)、求证: ;(3)、过点A作AE∥PC交⊙O于点E,交CD于点F,连接BE,若sin∠P= ,CF=5,求BE的长.27. 抛物线y=﹣x2+bx+c经过点A、B、C,已知A(﹣1,0),C(0,3). (1)、求抛物线的解析式;(2)、如图1,P为线段BC上一点,过点P作y轴平行线,交抛物线于点D,当△BDC的面积最大时,求点P的坐标;(3)、如图2,抛物线顶点为E,EF⊥x轴于F点,M(m,0)是x轴上一动点,N是线段EF上一点,若∠MNC=90°,请指出实数m的变化范围,并说明理由.
(1)、求抛物线的解析式;(2)、如图1,P为线段BC上一点,过点P作y轴平行线,交抛物线于点D,当△BDC的面积最大时,求点P的坐标;(3)、如图2,抛物线顶点为E,EF⊥x轴于F点,M(m,0)是x轴上一动点,N是线段EF上一点,若∠MNC=90°,请指出实数m的变化范围,并说明理由.