2018-2019学年初中数学华师大版九年级下册27.2.3切线 同步练习
试卷更新日期：2019-06-17 类型：同步测试
一、选择题
-
1. 如图，△ABC中，AB=5，BC=3，AC=4，以点C为圆心的圆与AB相切，则⊙C的半径为（ ）
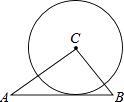A、2.3 B、2.4 C、2.5 D、2.62. 如图，点P在⊙O外，PA、PB分别与⊙O相切于A、B两点，∠P=50°，则∠AOB等于（ ）
A、150° B、130° C、155° D、135°3. 如图，AB是⊙O的弦，AC是⊙O切线，A为切点，BC经过圆心．若∠B=20°，则∠C的大小等于（ ）
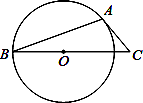A、20° B、25° C、40° D、50°4.如图，在⊙O的内接四边形ABCD中，AB是直径，∠BCD=120°，过D点的切线PD与直线AB交于点P，则∠ADP的度数为（ ）
A、40° B、35° C、30° D、45°5. 如图，AB是⊙O的弦，AO的延长线交过点B的⊙O的切线于点C，如果∠ABO=20°，则∠C的度数是（ ）
A、70° B、50° C、45° D、20°6. 如图，在⊙O中，AB为直径，BC为弦，CD为切线，连接OC．若∠BCD=50°，则∠AOC的度数为（ ）
A、40° B、50° C、80° D、100°7. 已知⊙O的半径为5，直线l是⊙O的切线，则点O到直线l的距离是（ ）A、2.5 B、3 C、5 D、108. 如图，一个边长为4cm的等边三角形ABC的高与⊙O的直径相等．⊙O与BC相切于点C ， 与AC相交于点E ， 则CE的长为（ ）
A、4cm B、3cm C、2cm D、1.5cm9. 如图，AB是⊙O直径，点C在⊙O上，AE是⊙O的切线，A为切点，连接BC并延长交AE于点D ． 若∠AOC=80°，则∠ADB的度数为（ ）
A、40° B、50° C、60° D、20°10. 如图，PA和PB是⊙O的切线，点A和B的切点，AC是⊙O的直径，已知∠P=40°，则∠ACB的大小是（ ）
A、40° B、60° C、70° D、80°11. 如图，AC是⊙O的切线，切点为C ， BC是⊙O的直径，AB交⊙O于点D ， 连接OD ． 若∠BAC=55°，则∠COD的大小为（ ）
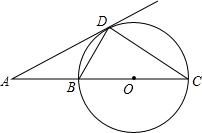
A、70° B、60° C、55° D、35°12. 如图，PA、PB分别与⊙O相切于A、B两点，若∠C=65°，则∠P的度数为（ ）
A、65° B、130° C、50° D、100°13. 如图，BC是⊙O的直径，AD是⊙O的切线，切点为D，AD与CB的延长线交于点A，∠C=30°，给出下面四个结论：①AD=DC；②AB=BD；③AB= BC；④BD=CD，
其中正确的个数为（ ）
A、4个 B、3个 C、2个 D、1个14. 我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”．如图，直线l：y=kx+4 与x轴、y轴分别交于A，B，∠OAB=30°，点P在x轴上，⊙P与l相切，当P在线段OA上运动时，使得⊙P成为整圆的点P个数是（ ）
A、6 B、8 C、10 D、1215.如图，已知PA、PB是⊙O的切线，A、B为切点，AC是⊙O的直径，∠P=40°，则∠BAC的大小是（ ）
A、70° B、40° C、50° D、20°二、填空题
-
16. 如图，AB为⊙O的直径，延长AB至点D，使BD=OB，DC切⊙O于点C，点B是 的中点，弦CF交AB于点E.若⊙O的半径为2，则CF=.
17. 如图，AB是⊙O的直径，点C在AB的延长线上，CD与⊙O相切于点D，若∠C=20°，则∠CDA=°.
18. 如图，AB是⊙O的直径，且经过弦CD的中点H，过CD延长线上一点E作⊙O的切线，切点为F.若∠ACF=65°，则∠E=.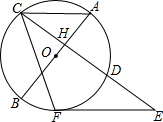
19.如图，PA是⊙O的切线，切点为A ， PO的延长线交⊙O于点B ． 若∠ABP=33°，则∠P=°．
20.如图，在△ABC中，AB=AC ， ∠B=30°，以点A为圆心，以3cm为半径作⊙A ， 当AB=cm时，BC与⊙A相切．
三、解答题
-
21. 已知在△ABC中，∠B=90°，以AB上的一点O为圆心，以OA为半径的圆交AC于点D，交AB于点E.
(1)、求证：AC•AD=AB•AE；(2)、如果BD是⊙O的切线，D是切点，E是OB的中点，当BC=2时，求AC的长.22. 如图，在Rt△ACB中，∠ACB=90°，点O是AC边上的一点，以O为圆心，OC为半径的圆与AB相切于点D，连接OD.
(1)、求证：△ADO∽△ACB(2)、若⊙O的半径为1，求证：AC=AD•BC.23. 如图，在△ABC中，∠B=60°，⊙O是△ABC的外接圆，过点A作⊙O的切线，交CO的延长线于点M，CM交⊙O于点D.
(1)、求证：AM=AC；(2)、若AC=3，求MC的长.
