2018-2019学年初中数学华师大版九年级下册27.2.2直线与圆的位置关系 同步练习
试卷更新日期：2019-06-17 类型：同步测试
一、选择题
-
1. 如图，∠O=30°，C为OB上一点，且OC=6，以点C为圆心，半径为3的圆与OA的位置关系是（ ）A、相离 B、相交 C、相切 D、以上三种情况均有可能2. 如图，两个同心圆，大圆的半径为5，小圆的半径为3，若大圆的弦AB与小圆有公共点，则弦AB的取值范围是（ ）
A、8≤AB≤10 B、8＜AB≤10 C、4≤AB≤5 D、4＜AB≤53. 在△ABC中，∠A=90°，AB=3cm，AC=4cm，若以A为圆心3cm为半径作⊙O，则BC与⊙O的位置关系是（ ）A、相交 B、相离 C、相切 D、不能确定4. 已知⊙O的直径是10，圆心O到直线l的距离是5，则直线l和⊙O的位置关系是（ ）A、相离 B、相交 C、相切 D、外切5. ⊙O的半径为7cm，圆心O到直线l的距离为8cm，则直线l与⊙O的位置关系是（ ）A、相交 B、内含 C、相切 D、相离6. 已知⊙O的直径是16cm，点O到同一平面内直线l的距离为9cm，则直线l与⊙O的位置关系是（ ）A、相交 B、相切 C、相离 D、无法判断7. 已知⊙O半径为3，M为直线AB上一点，若MO=3，则直线AB与⊙O的位置关系为（ ）A、相切 B、相交 C、相切或相离 D、相切或相交8.如图，平面直角坐标系中，已知P（6，8），M为OP中点，以P为圆心，6为半径作⊙P，则下列判断正确的有（ ）
①点O在⊙P外；②点M在⊙P上；③x轴与⊙P相离；④y轴与⊙P相切．
A、1个 B、2个 C、3个 D、4个9.如图，△ABC中，AB=3，AC=4，BC=5，D、E分别是AC、AB的中点，则以DE为直径的圆与BC的位置关系是（ ）
A、相切 B、相交 C、相离 D、无法确定10. 已知⊙O的半径为6cm，圆心O到直线l的距离为5cm，则直线l与⊙O的交点个数为（ ）A、0 B、l C、2 D、无法确定11. 已知⊙O的半径r=3，设圆心O到一条直线的距离为d，圆上到这条直线的距离为2的点的个数为m，给出下列命题：①若d＞5，则m=0；②若d=5，则m=1；③若1＜d＜5，则m=3；④若d=1，则m=2；⑤若d＜1，则m=4.
其中正确命题的个数是（ ）
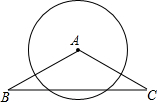
A、1 B、2 C、3 D、512. 已知在平面直角坐标系中，圆P的圆心坐标为（4，5），半径为3个单位长度，把圆P沿水平方向向左平移d个单位长度后恰好与y轴相切，则d的值是（ ）A、1 B、2 C、2或8 D、1或713. 已知⊙O的半径为5，直线AB与⊙O有交点，则直线AB到⊙O的距离可能为（ ）A、5.5 B、6 C、4.5 D、714. 已知△ABC中，AB=AC=6cm，BC=8cm，以点A为圆心，以4cm长为半径作圆，则⊙A与BC的位置关系是（ ）
A、相离 B、相切 C、相交 D、外离15. 已知⊙O与直线AB相交，且圆心O到直线AB的距离是方程2x-1=4的根，则⊙O的半径可为（ ）.A、1 B、2 C、2.5 D、3二、填空题
-
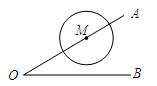
16. 在Rt△ABC中，AC=3，BC=4．如果以点C为圆心，r为半径的圆与斜边AB只有一个公共点，那么半径r的取值范围是 ．17. 在直角坐标平面内，圆心O的坐标是（3，-5），如果圆O经过点（0，-1），那么圆O与x轴的位置关系是.18. 已知⊙O的半径为10cm，如果一条直线和圆心O的距离为10cm，那么这条直线和这个圆的位置关系为 ．19. 如图，已知∠BOA=30°，M为OA边上一点，以M为圆心、2cm为半径作⊙M.点M在射线OA上运动，当OM=5cm时，⊙M与直线OB的位置关系是.
20. 已知⊙O的半径为R，点O到直线m的距离为d，R、d是方程x2-4x+a=0的两根，当直线m与⊙O相切时，a=.三、解答题
-
21. 设⊙O的圆心O到直线的距离为d，半径为r，且直线与⊙O相切.d，r是一元二次方程（m+9）x2-（m+6）x+1=0的两根，求m的值.22.
如图，已知⊙O与BC相切，点C不是切点，AO⊥OC，∠OAC=∠ABO，且AC=BO，判断直线AB与⊙O的位置关系，并说明理由．
23. 如图在Rt△ABC中，∠C=90°，点O在AB上，以O为圆心，OA长为半径的圆与AC、AB，分别交于点D、E，且∠CBD=∠A；
(1)、判断直线BD与⊙O的位置关系，并证明你的结论；(2)、若AD：AO=6：5，BC=2，求BD的长.
