浙教版2018-2019学年八年级下学期数学期末模拟试卷

试卷更新日期：2019-06-14 类型：期末考试

进入出卷网下载

一、单选题

1. 下列计算正确的是（）

A、 $\sqrt{4 + 9}$ ＝ $\sqrt{4}$ ＋ $\sqrt{9}$ B、3 $\sqrt{2}$ － $\sqrt{2}$ ＝3 C、 $\sqrt{14}$ × $\sqrt{7}$ ＝7 $\sqrt{2}$ D、 $\sqrt{24}$ ÷ $\sqrt{3}$ ＝2 $\sqrt{3}$

查看试题解析
2. 为使 $\sqrt{2 x + 4} - \frac{3}{3 x - 6}$ 有意义，x的取值范围是(　　)

A、 $x \geq - 2$ 且x≠2 B、 $x > - 2$ 且x≠2 C、 $x > 2$ D、x>2或 $x \leq - 2$

查看试题解析

3. “十•一”黄金周期间，某风景区在7天假期中，共接待游客的人数（单位：万人）统计如下表：

日期	10月1日	10月2日	10月3日	10月4日	10月5日	10月6日	10月7日
人数	1.2	2	2.5	2	1.2	2	0.6

其中众数和中位数分别是（）

A、1.2，2 B、2，2.5 C、2，2 D、1.2，2.5

查看试题解析

4. 已知反比例函数y＝﹣ $\frac{6}{x}$ ，下列结论中不正确的是（）

A、图象必经过点（﹣3，2） B、图象位于第二、四象限 C、若x＜﹣2，则0＜y＜3 D、在每一个象限内，y随x值的增大而减小

查看试题解析
5. 已知反比例函数y=- $\frac{2}{x}$ ，点A(a-b，2），B(a-c，3）在这个函数图象上，下列对于a，b，c的大小判断正确的是（）

A、a<b＜c B、a＜c＜b C、c<b＜a D、b＜c＜a

查看试题解析
6. 下列判定正确的是（）

A、 $\sqrt{0.1}$ 是最简二次根式 B、方程 $x^{2} + 1 = 0$ 不是一元二次方程 C、已知甲、乙两组数据的平均数分别是 ${\bar{x}}_{甲} = 80$ ， ${\bar{x}}_{乙} = 90$ ，方差分别是 $S_{甲}^{2} = 10$ ， $S_{乙}^{2} = 5$ ，则甲组数据的波动较小 D、若 $\sqrt{2 x - 5}$ 与 $\sqrt{5 - 2 x}$ 都有意义，则 $\sqrt{2 x - 5} + \sqrt{5 - 2 x} + 2 x$ 的值为5

查看试题解析
7. 将正方形纸片按如图折叠，若正方形纸片边长为4，则图片中MN的长为 $($ 　　 $)$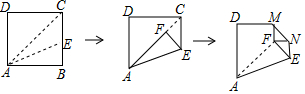

A、1 B、2 C、 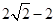D、

查看试题解析
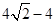8. 如图，四边形ABCD是平行四边形，下列说法不正确的是（）

A、当AC＝BD时，四边形ABCD是矩形 B、当AB＝BC时，四边形ABCD是菱形 C、当AC⊥BD时，四边形ABCD是菱形 D、当∠DAB＝90°时，四边形ABCD是正方形

查看试题解析
9. 正比例函数 $y = x$ 与反比例函数 $y = \frac{1}{x}$ 的图象相交于A，C两点，AB⊥x轴于点B，CD⊥x轴于点D（如图），则四边形ABCD的面积为（）

A、1 B、 $\frac{3}{2}$ C、2 D、 $\frac{5}{2}$

查看试题解析
10. 如图，在边长4的正方形ABCD中，E是边BC的中点，将△CDE沿直线DE折叠后，点C落在点F处，再将其打开、展平，得折痕DE．连接CF、BF、EF，延长BF交AD于点G．则下列结论：①BG＝DE；②CF⊥BG；③sin∠DFG＝ $\frac{1}{2}$ ；④S_△DFG＝ $\frac{12}{5}$ ，其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 化简： $\sqrt{x - 2 \sqrt{x - 1}} - \sqrt{3 - x - 2 \sqrt{2 - x}}$ = ．

查看试题解析
12. 一个菱形的两条对角线长分别为3cm，4cm，这个菱形的面积S=.

查看试题解析
13. 如图，在平行四边形ABCD中，AB＝3，BC＝5，∠B的平分线BE交AD于点E，则DE的长为.

查看试题解析
14. 如图，矩形ABCD的边AB与y轴平行，顶点A的坐标为（1，2），点B与点D在反比例函数 $y = \frac{6}{x} (x > 0)$ 的图象上，则点C的坐标为．

查看试题解析
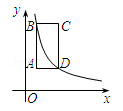15. 若m、n是一元二次方程x²﹣5x﹣2=0的两个实数根，则m+n﹣mn= ．

查看试题解析
16. 已知方程x²+（a﹣3）x+3＝0在实数范围内恒有解，并且恰有一个解大于1小于2，a的取值范围是．

查看试题解析

三、综合题

17. 计算： $\sqrt{9} + \sqrt[3]{- 8} + {(π - 3)}^{0} - | - 2 | + {(- 1)}^{2}$ ．

查看试题解析
18. 解方程：

(1)、x(2x－7)＝2x

(2)、 $2 x^{2} + 4 x - 3 = 0$

查看试题解析

19. 某公司需招聘一名员工，对应聘者甲、乙、丙从笔试、面试、体能三个方面进

行量化考核，甲、乙、丙各项得分如下表：

考核人员	笔试	面试	体能	平均分
甲	83	79	90	84
乙	86	80	x	80
丙	80	90	73	y

(1)、根据表格中的数据信息，求得x=；y=.

(2)、该公司规定：笔试、面试、体能得分分别不得低于80分，80分，70分，并按50%，30%，20%的比例计入总分.请你根据规定，计算说明谁将被录用.

查看试题解析

20. 某公园要在一块长40m，宽30m的长方形空地上建成一个矩形花园，要求在花园中修三条纵向平行和两条横向平行的宽度相同的小道，剩余的地方种植花草.如图所示，要使种植花草的面积为500m² ，那么小道进出口的宽度应为多少米？

查看试题解析
21. 如图，点B、F、C、E在一条直线上，FB=CE，AB∥ED，AC∥FD，AD交BE于O．求证：AD与BE互相平分．

查看试题解析
22. 如图，点 $A (m ， m + 1) ， B (m + 3 ， m - 1)$ 都在反比例函数 $y = \frac{k}{x}$ 的图象上．

(1)、求 $m ， k$ 的值；

(2)、如果 $M$ 为 $x$ 轴上一点， $N$ 为 $y$ 轴上一点，以点 $A ， B ， M ， N$ 为顶点的四边形是平行四边形，试求直线 $M N$ 的函数表达式；

(3)、将线段 $A B$ 沿直线 $y = k x + b$ 进行对折得到线段 $A_{1} B_{1}$ ，且点 $A_{1}$ 始终在直线 $O A$ 上，当线段 $A_{1} B_{1}$ 与 $x$ 轴有交点时，则 $b$ 的取值范围为（直接写出答案）

查看试题解析
23.

(1)、问题发现：
如图1，在正方形ABCD中，点E、F分别是边BC、AB上的点，且CE=BF，连接DE，过点E作EG⊥DE，使EG=DE，连接FG，FC，请判断：FG与CE的数量关系是，位置关系是．

(2)、拓展探究：
如图2，若点E、F分别是CB、BA延长线上的点，其它条件不变，（1）中结论是否仍然成立？请出判断判断予以证明；

(3)、类比延伸：
如图3，若点E、F分别是BC、AB延长线上的点，其它条件不变，（1）中结论是否仍然成立？请直接写出你的判断．

查看试题解析
24. 如图，反比例函数 $y = \frac{k}{x}$ 与y＝mx交于A，B两点，设点A、B的坐标分别为A（x₁ ， y₁），B（x₂ ， y₂），S＝|x₁y₁|，且 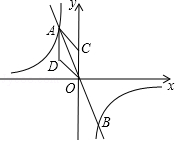$\frac{3}{s - 1} = \frac{4}{s}$ ，

(1)、求k的值；

(2)、当m变化时，代数式 $\frac{(m^{2} - 1) x_{1} y_{2}}{{(m + 1)}^{2}} + \frac{2 x_{2} y_{1}}{m + 1}$ 是否为一个固定的值？若是，求出其值，若不是，请说理由；

(3)、点C在y轴上，点D的坐标是（﹣1， $\frac{3}{2}$ ），若将菱形ACOD沿x轴负方向平移m个单位，在平移过程中，若双曲线与菱形的边AD始终有交点，请直接写出m的取值范围．

查看试题解析