浙教版2018-2019学年七年级下学期数学期末模拟试卷

试卷更新日期：2019-06-14 类型：期末考试

进入出卷网下载

一、选择题

1. 若分式 $\frac{x - 2}{x + 3}$ 有意义，则x的取值范围是（　　）

A、x≠﹣3 B、x≥﹣3 C、x≠﹣3且 x≠2 D、x≠2

查看试题解析
2. 下列运算正确的是（）

A、 ${(a^{2})}^{3} = a^{5}$ B、 $a^{2} a^{4} = a^{8}$ C、 $a^{6} \div a^{3} = a^{2}$ D、 ${(2 a^{2} b)}^{3} = 8 a^{6} b^{3}$

查看试题解析
3. 计算 $\frac{1}{x - 1} -$ $\frac{x}{x - 1}$ 的结果为（）

A、1 B、2 C、﹣1 D、﹣2

查看试题解析
4. 已知a-b=1，a=5，则a²-ab等于（）

A、1 B、4 C、5 D、6

查看试题解析
5. 如图，与∠B互为同旁内角的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 比较3⁵⁵ ， 4⁴⁴ ， 5³³的大小，正确的是（）

A、 4⁴⁴>3⁵⁵>5³³ B、5³³>4⁴⁴>3⁵⁵ C、3⁵⁵>4⁴⁴>5³³ D、3⁵⁵>5³³>4⁴⁴

查看试题解析
7. 某次知识竞赛共有20道题，规定：每答对一题得+5分，每答错一题得-2分，不答的题得0分。已知圆圆这次竞赛得了60分，设圆圆答对了 $x$ 道题，答错了 $y$ 道题，则（）

A、 $x - y = 20$ B、 $x + y = 20$ C、 $5 x - 2 y = 60$ D、 $5 x + 2 y = 60$

查看试题解析
8. 如图是一张长方形的拼图卡片，它被分割成4个大小不同的正方形和一个长方形，若要计算整张卡片的周长，则只需知道哪个正方形的边长即可 $($ $)$

A、 $④$ B、 $③$ C、 $②$ D、 $①$

查看试题解析
9. 如图，把一张长方形纸片ABCD沿EF折叠后，ED与BC交点为G，D，C分别在M、N的位置上，若∠2-∠1=40°，则∠EFC的度数为（）

A、115° B、125° C、135° D、145°

查看试题解析
10. 不论x、y为什么实数，代数式x²+y²+2x﹣4y+7的值（）

A、总不小于2 B、总不小于7 C、可为任何实数 D、可能为负数

查看试题解析

二、填空题

11. 若分式 $\frac{| a | - 2}{(a - 2) (a + 3)}$ 的值为0，则a=.

查看试题解析
12. 分解因式：x²﹣2x﹣2y²+4y﹣xy= ．

查看试题解析
13. 当x＝m或x＝n（m≠n）时，代数式x²﹣2x+4的值相等，则当x＝m+n时，代数式x²﹣2x+4的值为．

查看试题解析
14. 在日常生活中，如取款、上网需要密码，有一种因式分解法产生密码，例如x⁴－y⁴＝(x－y)(x＋y)(x²＋y²)，当x＝9，y＝9时，x－y＝0，x＋y＝18，x²＋y²＝162，则密码018162. 对于多项式4x³－xy² ，取x＝10，y＝10，用上述方法产生密码是(写出一个即可).

查看试题解析
15. 任何实数a，可用[a]表示不超过a的最大整数，如[2]=2，[3.7]=3，现对72进行如下操作： $72 \overset{第一次}{\to} [\sqrt{72}] = 8 \overset{第二次}{\to} [\sqrt{8}] = 2 \overset{第三次}{\to} [\sqrt{2}] = 1$ ，这样对72只需进行3次操作后变为1，类似地：对325只需进行次操作后变为1.

查看试题解析
16. 如图1，将一个边长为a的正方形纸片剪去两个小矩形，得到一个“ ”的图案，如图2所示，再将剪下的两个小矩形拼成一个新的矩形，如图3所示，则新矩形的周长可表示为．

查看试题解析

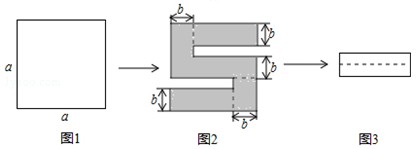
三、解答题

17.

(1)、分解因式：3x³﹣27x

(2)、 $\frac{2}{x - 2} = \frac{3}{x}$

查看试题解析
18. 已知A＝ $\frac{x^{2} + 2 x}{x^{2} - 1}$ ﹣ $\frac{x}{x - 1}$ ，B＝（x+2）（x+4）+1．

(1)、化简A，并对B进行因式分解；

(2)、当B＝0时，求A的值．

查看试题解析
19. 已知 ${\begin{cases} x = 2 \\ y = 3 \end{cases}$ 是方程组 ${\begin{cases} m x + (n + 2) y = 8 \\ (m - 1) x + (1 - n) y = 7 \end{cases}$ 的解。求m，n的值。

查看试题解析
20.
如图：在正方形网格中有一个△ABC，按要求进行下列作图（只借助于网格，需写出结论）：

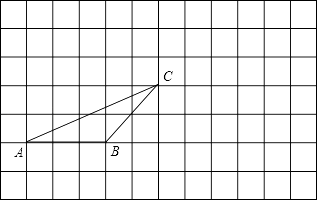(1)、过点A画出BC的平行线；

(2)、画出先将△ABC向右平移5格，再向上平移3格后的△DEF；

查看试题解析
21. 已知如图，已知∠1＝∠2，∠C＝∠D．

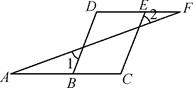(1)、判断BD与CE是否平行，并说明理由；

(2)、说明∠A＝∠F的理由．

查看试题解析

22. 为了解同学们每月零花钱数额，校园小记者随机调查了本校部分学生，并根据调查结果绘制出如下不完整的统计图表：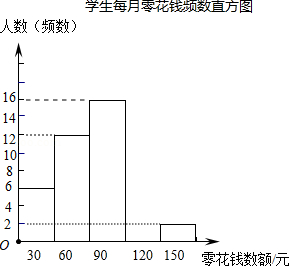

请根据以上图表，解答下列问题：

零花钱数额x/元	人数（频数）	频率
0≤x＜30	6	0.15
30≤x＜60	12	0.30
60≤x＜90	16	0.40
90≤x＜120	b	0.10
120≤x＜150	2	a

(1)、这次被调查的人数共有人，a= ．

(2)、计算并补全频数分布直方图；

(3)、请估计该校1500名学生中每月零花钱数额低于90元的人数．

查看试题解析

23. 育新中学组织20个团员分成两组分别去A，B两地开展植树活动，去A地植树人数不超过10人时，每人能植树6棵，去A地植树人数超过10人时，每人只能植树4棵.在B池的团员每人植树5棵。（每个团员所植树的棵数均满足要求）

(1)、若这批团员中，去A地的人数超过10人，本次植树活动共植树86棵。问去A，B两地团员各多少人?

(2)、小明同学说“经统计，本次我们20个团员共植树96棵”，你认为小明同学的统计有问题吗?请你通过计算说明.

(3)、当去A，B闭地的团炎到达目的地后，B地团员发现还有8位大人义工也来植树，在B地原来团员同学每人可以植树5棵，大人每人植树10标，如果抽取一部分大人协助指导团员植树，这样B组团员每人可以植树8棵，被抽取的大人每人只能植树5棵；就团员和大人在B地的植树的总数来看。有大人协助比没有大人协助多了15棵，求到B地的团员人数。

查看试题解析
24. 如图1，已知直线CD∥EF，点A、B分别在直线CD与EF上．P为两平行线间一点．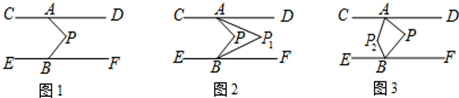

(1)、若∠DAP=40°，∠FBP=70°，则∠APB= ．

(2)、猜想∠DAP，∠FBP，∠APB之间有什么关系？并说明理由．

(3)、利用(2)的结论解答：
①如图2，AP₁、BP₁分别平分∠DAP、∠FBP，请你写出∠P与∠P₁的数量关系，并说明理由．

②如图3，AP₂、BP₂分别平分∠CAP、∠EBP，若∠APB=β，求∠AP₂B(用含β的代数式表示)．

查看试题解析