2019年高考数学真题分类汇编专题20：参数方程、不等式与矩阵

试卷更新日期：2019-06-14 类型：二轮复习

进入出卷网下载

一、单选题

1. 已知直线l的参数方程为 ${\begin{cases} x = 1 + 3 t \\ y = 2 + 4 t \end{cases}$ （t为参数），则点（1，0）到直线l的距离是（）

A、 $\frac{1}{5}$ B、 $\frac{2}{5}$ C、 $\frac{4}{5}$ D、 $\frac{6}{5}$

查看试题解析

二、填空题

2. 设 $x > 0, y > 0, x + 2 y = 4$ ，则 $\frac{(x + 1) (2 y + 1)}{x y}$ 的最小值为.

查看试题解析
3. 设 $x \in R$ ，使不等式 $3 x^{2} + x - 2 < 0$ 成立的 $x$ 的取值范围为.

查看试题解析
4. 设 $x > 0, y > 0, x + 2 y = 5$ ，则 $\frac{(x + 1) (2 y + 1)}{\sqrt{x y}}$ 的最小值为.

查看试题解析

三、解答题

5. 在极坐标系中，已知两点 $A (3, \frac{π}{4}), B (\sqrt{2}, \frac{π}{2})$ ，直线l的方程为 $ρ \sin (θ + \frac{π}{4}) = 3$ .

(1)、求A ， B两点间的距离；

(2)、求点B到直线l的距离.

查看试题解析
6. [选修4-4：坐标系与参数方程]
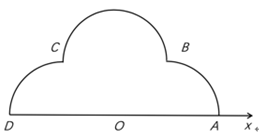如图，在极坐标系Ox中，A（2，0），B（ $\sqrt{2}$ ， $\frac{π}{4}$ ），C（ $\sqrt{2}$ ， $\frac{3 π}{4}$ ），D（2，π），弧 $\overset{⌢}{A B}$ ， $\overset{⌢}{B C}$ ， $\overset{⌢}{C D}$ 所在圆的圆心分别是（1，0），（1， $\frac{π}{2}$ ），（1，π），曲线M₁是弧 $\overset{⌢}{A B}$ ，曲线M₂是弧 $\overset{⌢}{B C}$ ，曲线M₃是弧 $\overset{⌢}{C D}$ 。

(1)、分别写出M₁ ， M₂ ， M₃的极坐标方程；

(2)、曲线由M₁ ， M₂ ， M₃构成，若点P在M上，且|OP|= $\sqrt{3}$ ，求P的极坐标。

查看试题解析
7. [选修4-4：坐标系与参数方程]在极坐标系中，O为极点，点 $M (ρ_{0} ， θ_{0}) (ρ_{0} > 0)$ 在曲线 $C ： ρ = 4 s i n θ$ 上，直线l过点 $A (4 ， 0)$ 且与 $O M$ 垂直，垂足为P.

(1)、当 $θ_{0} = \frac{π}{3}$ 时，求 $ρ_{0}$ 及l的极坐标方程；

(2)、当M在C上运动且P在线段OM上时，求P点轨迹的极坐标方程.

查看试题解析
8. 在直角坐标系xOy中，曲线C的参数方程为 ${\begin{cases} x = \frac{1 - t^{2}}{1 + t^{2}} \\ y = \frac{4 t}{1 + t^{2}} \end{cases}$ （t为参数）。以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，直线l的极坐标方程为2ρcosθ+ $\sqrt{3}$ ρsinθ+11=0。

(1)、求C和l的直角坐标方程；

(2)、求C上的点到l距离的最小值。

查看试题解析
9. 在直角坐标系xOy中，曲线C的参数方程为 ${\begin{cases} x = \frac{1 - t^{2}}{1 + t^{2}} \\ y = \frac{4 t}{1 + t^{2}} \end{cases}$ （t为参数）。以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，直线l的极坐标方程为2ρcosθ+ $\sqrt{3}$ ρsinθ+11=0。

(1)、求C和l的直角坐标方程；

(2)、求C上的点到l距离的最小值。

查看试题解析
10. 设 $x \in R$ ，解不等式 $| x |+|2 x - 1|>2$ .

查看试题解析
11. 设x，y，z∈R，且x+y+z=1，

(1)、求（x-1）²+（y+1）²+（z-1）²的最小值；

(2)、若（x-2）²+（y-1）²+（z-2）²≥ $\frac{1}{3}$ 成立，证明：a≤-3或a≥-1。

查看试题解析
12. 已知 $f (x) = | x - a | x + | x - 2 | (x - a) .$

(1)、当 $a = 1$ 时，求不等式 $f (x) < 0$ 的解集；

(2)、若 $x \in (- \infty ， 1 ）$ 时， $f (x) < 0$ ，求 $a$ 的取值范围.

查看试题解析
13. 已知a，b，c为正数，且满足abc=1。证明：

(1)、 $\frac{1}{a} + \frac{1}{b} + \frac{1}{c} \leq a^{2} + b^{2} + c^{2}$ ；

(2)、(a+b)³+(b+c)³+(c+a)³≥24。

查看试题解析
14. A.[选修4-2：矩阵与变换]
已知矩阵 $A = [\begin{array}{l} 3 & 1 \\ 2 & 2 \end{array}]$

(1)、求A²；

(2)、求矩阵A的特征值.

查看试题解析