2019年高考数学真题分类汇编专题17：平面解析几何（综合题）

试卷更新日期：2019-06-14 类型：二轮复习

进入出卷网下载

一、解答题

1. 如图，在平面直角坐标系xOy中，椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的焦点为F₁（–1、0），F₂（1，0）．过F₂作x轴的垂线l ，在x轴的上方，l与圆F₂： ${(x - 1)}^{2} + y^{2} = 4 a^{2}$ 交于点A ，与椭圆C交于点D.连结AF₁并延长交圆F₂于点B ，连结BF₂交椭圆C于点E ，连结DF₁ ．已知DF₁= $\frac{5}{2}$ ．

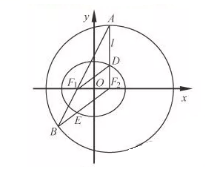(1)、求椭圆C的标准方程；

(2)、求点E的坐标．

查看试题解析
2. 如图，已知点F（1，0）为抛物线y²=2px（p>0）的焦点.过点F的直线交抛物线A，B两点，点C在抛物线上，使得△ABC的重心G在x轴上，直线AC交x轴于点Q，且Q在点F右侧，记△AFG，△CQG的面积分别为S₁_，S₂.

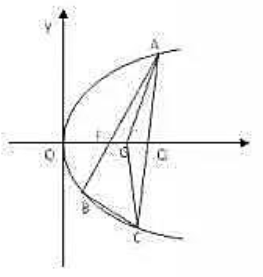(1)、求P的值及抛物线的准线方程.

(2)、求 $\frac{S_{1}}{S_{2}}$ 的最小值及此时点G点坐标.

查看试题解析
3. 设椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左焦点为 $F$ ，左顶点为 $A$ ，顶点为B.已知 $\sqrt{3} | O A | = 2 | O B |$ （ $O$ 为原点）.
（Ⅰ）求椭圆的离心率；

（Ⅱ）设经过点 $F$ 且斜率为 $\frac{3}{4}$ 的直线 $l$ 与椭圆在 $x$ 轴上方的交点为 $p$ ，圆 $C$ 同时与 $x$ 轴和直线 $l$ 相切，圆心 $C$ 在直线 $x = 4$ 上，且 $O C ∥ A P$ ，求椭圆的方程.

查看试题解析
4. 设椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左焦点为 $F$ ，上顶点为 $B$ .已知椭圆的短轴长为4，离心率为 $\frac{\sqrt{5}}{5}$ .
（Ⅰ）求椭圆的方程；

（Ⅱ）设点 $P$ 在椭圆上，且异于椭圆的上、下顶点，点 $M$ 为直线 $P B$ 与 $x$ 轴的交点，点 $N$ 在 $y$ 轴的负半轴上.若 $| O N | = | O F |$ （ $O$ 为原点），且 $O P ⊥ M N$ ，求直线 $P B$ 的斜率.

查看试题解析
5. 已知曲线C：y= $\frac{x^{2}}{2}$ ，D为直线y= $- \frac{1}{2}$ 上的动点，过D作C的两条切线，切点分别为A ， B.

(1)、证明：直线AB过定点：

(2)、若以E(0， $\frac{5}{2}$ )为圆心的圆与直线AB相切，且切点为线段AB的中点，求该圆的方程.

查看试题解析
6. 已知曲线C: $y = \frac{x^{2}}{2}$ ，D为直线y=- $\frac{1}{2}$ 的动点，过D作C的两条切线，切点分别为A，B.

(1)、证明：直线AB过定点；

(2)、若以E（0， $\frac{5}{2}$ ）为圆心的圆与直线AB相切，且切点为线段AB的中点，求四边形ADBE的面积.

查看试题解析
7. 已知 $F_{1}, F_{2}$ 是椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ $(a > b > 0)$ 的两个焦点， $P$ 为 $C$ 上的点， $O$ 为坐标原点。

(1)、若 $△ P O F_{2}$ 为等边三角形，求 $C$ 的离心率；

(2)、如果存在点P，使得 $P F_{1} ⊥ P F_{2}$ ，且 $△ F_{1} P F_{2}$ 的面积等于16，求 $b$ 的值和a的取值范围。

查看试题解析
8. 已知点A(−2,0)，B(2,0)，动点M(x,y)满足直线AM与BM的斜率之积为− $\frac{1}{2}$ .记M的轨迹为曲线C.

(1)、求C的方程，并说明C是什么曲线；

(2)、过坐标原点的直线交C于P，Q两点，点P在第一象限，PE⊥x轴，垂足为E，连结QE并延长交C于点G.
（i）证明： $△ P Q G$ 是直角三角形；

（ii）求 $△ P Q G$ 面积的最大值.

查看试题解析
9. 已知椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ 的右焦点为（1.0），且经过点A（0，1）.
（I）求椭圆C的方程；

（II）设O为原点，直线l：y=kx+t（t≠±1）与椭圆C交于两个不同点P，Q，直线AP与x轴交于点M，直线AQ与x轴交于点N，|OM|·|ON|=2，求证：直线l经过定点.

查看试题解析
10. 已知抛物线C：x²=-2py经过点（2，-1）.
（I）求抛物线C的方程及其准线方程；

（II）设O为原点，过抛物线C的焦点作斜率不为0的直线l交抛物线C于两点M，N，直线y=-1分别交直线OM，ON于点A和点B.求证：以AB为直径的圆经过y轴上的两个定点.

查看试题解析
11. 已知点A，B关于坐标原点O对称，|AB|=4，⊙M过点A，B且与直线x+2=0相切。

(1)、若A在直线x+y=0上，求⊙M的半径。

(2)、是否存在定点P，使得当A运动时，|MA|-|MP|为定值？并说明理由。

查看试题解析
12. 已知抛物线C：y²=3x的焦点为F，斜率为 $\frac{3}{2}$ 的直线l与C的交点为A，B，与x轴的交点为P。

(1)、若|AF|+|BF|=4,求l的方程：

(2)、若 $\vec{A P} = 3 \vec{P B}$ ,求|AB|。

查看试题解析