2019年高考数学真题分类汇编专题16:空间几何
试卷更新日期:2019-06-14 类型:二轮复习
一、解答题
-
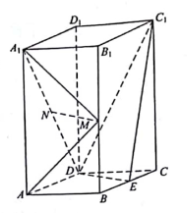
1. 如图,在直三棱柱ABC-A1B1C1中,D , E分别为BC , AC的中点,AB=BC .
求证:
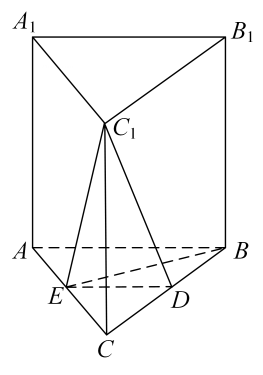
(1)、A1B1∥平面DEC1;(2)、BE⊥C1E .2. 如图,已知三棱柱ABC-A1B1C1 , 平面A1AC1C⊥平面ABC,∠ABC=90°.∠BAC=30°,A1A=A1C=AC,E,F分别是AC,A1B1的中点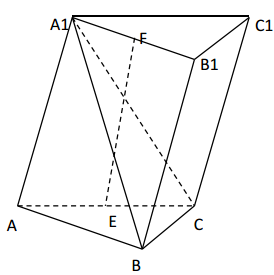 (1)、证明:EF⊥BC(2)、求直线EF与平面A1BC所成角的余弦值.3. 如图,在四棱锥 中,底面 为平行四边形, 为等边三角形,平面 平面 , , ,
(1)、证明:EF⊥BC(2)、求直线EF与平面A1BC所成角的余弦值.3. 如图,在四棱锥 中,底面 为平行四边形, 为等边三角形,平面 平面 , , ,
(Ⅰ)设 分别为 的中点,求证: 平面 ;
(Ⅱ)求证: 平面 ;
(Ⅲ)求直线 与平面 所成角的正弦值.
4. 如图, 平面 , , .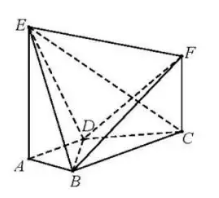
(Ⅰ)求证: 平面 ;
(Ⅱ)求直线 与平面 所成角的正弦值;
(Ⅲ)若二面角 的余弦值为 ,求线段 的长.
5. 图1是由矩形ADEB、 ABC和菱形BFGC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°.将其沿AB , BC折起使得BE与BF重合,连结DG , 如图2.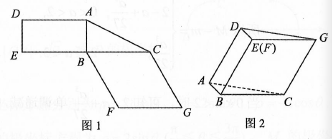 (1)、证明图2中的A , C , G , D四点共面,且平面ABC⊥平面BCGE;(2)、求图2中的四边形ACGD的面积.6. 图1是由矩形ADEB、Rt△ABC和菱形BFCC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°,将其沿AB,BC折起使得BE与BF重合,连结DC,如题2.
(1)、证明图2中的A , C , G , D四点共面,且平面ABC⊥平面BCGE;(2)、求图2中的四边形ACGD的面积.6. 图1是由矩形ADEB、Rt△ABC和菱形BFCC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°,将其沿AB,BC折起使得BE与BF重合,连结DC,如题2.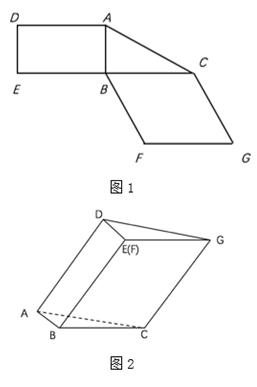 (1)、证明:图2中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;(2)、求图2中的二面角B-CG-A的大小.
(1)、证明:图2中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;(2)、求图2中的二面角B-CG-A的大小.
7. 如图,长方体 的底面 是正方形,点 在棱 上, 。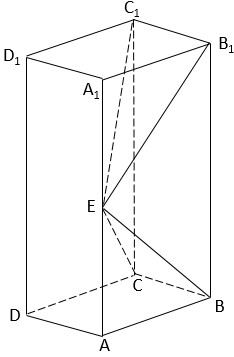 (1)、证明: ;(2)、若 , ,求四棱锥 的体积。8. 如图,长方体ABCD–A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.
(1)、证明: ;(2)、若 , ,求四棱锥 的体积。8. 如图,长方体ABCD–A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1. (1)、证明:BE⊥平面EB1C1;(2)、若AE=A1E,求二面角B–EC–C1的正弦值.9. 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,E为CD的中点.
(1)、证明:BE⊥平面EB1C1;(2)、若AE=A1E,求二面角B–EC–C1的正弦值.9. 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,E为CD的中点.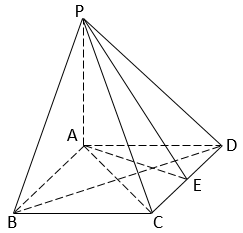
(Ⅰ)求证:BD⊥平面PAC;
(Ⅱ)若∠ABC=60°,求证:平面PAB⊥平面PAE;
(Ⅲ)棱PB上是否存在点F,使得CF∥平面PAE?说明理由.
10. 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD⊥CD,AD∥BC,PA=AD=CD=2,BC=3。E为PD的中点,点F在PC上,且 .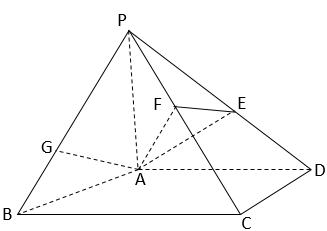
(I)求证:CD⊥平面PAD;
(II)求二面角F-AE-P的余弦值;
(III)设点G在PB上,且 .判断直线AG是否在平面AEF内,说明理由。