2019年高考数学真题分类汇编专题15：概率与统计（综合题）

1. 设 ${(1+x)}^n=a_0+a_{1}x+a_2{x}^2+\cdots +a_n{x}^n,n⩾4,n\in N^{*}$ .已知 $a_3^2=2a_2{a}_4$ .

2. 在平面直角坐标系xOy中，设点集 $A_n=\{(0,0),(1,0),(2,0),\dots ,(n,0)\}$ ， $B_n=\{(0,1),(n,1)\text{}},C_n=\{(0,2),(1,2),(2,2),\cdots ,(n,2)\},n\in N^{\ast }.$

令 $M_n=A_n\cup B_n\cup C_n$ .从集合M_n中任取两个不同的点，用随机变量X表示它们之间的距离.

3. 2019年，我国施行个人所得税专项附加扣除办法，涉及子女教育、继续教育、大病医疗、住房贷款利息或者住房租金、赡养老人等六项专项附加扣除.某单位老、中、青员工分别有 $72，108，120$ 人，现采用分层抽样的方法，从该单位上述员工中抽取25人调查专项附加扣除的享受情况.

（Ⅰ）应从老、中、青员工中分别抽取多少人？

（Ⅱ）抽取的25人中，享受至少两项专项附加扣除的员工有6人，分别记为 $A，B，C，D，E，F$ .享受情况如右表，其中“ ”表示享受，“×”表示不享受.现从这6人中随机抽取2人接受采访.

员工 项目	A	B	C	D	E	F
子女教育	○	○	×	○	×	○
继续教育	×	×	○	×	○	○
大病医疗	×	×	×	○	×	×
住房贷款利息	○	○	×	×	○	○
住房租金	×	×	○	×	×	×
赡养老人	○	○	×	×	×	○

（i）试用所给字母列举出所有可能的抽取结果；

（ii）设 $M$ 为事件“抽取的2人享受的专项附加扣除至少有一项相同”，求事件 $M$ 发生的概率.

4. 设甲、乙两位同学上学期间，每天7：30之前到校的概率均为 $\frac{2}{3}$ .假定甲、乙两位同学到校情况互不影响，且任一同学每天到校情况相互独立.

（Ⅰ）用 $X$ 表示甲同学上学期间的三天中7：30之前到校的天数，求随机变量 $X$ 的分布列和数学期望；

（Ⅱ）设 $M$ 为事件“上学期间的三天中，甲同学在7：30之前到校的天数比乙同学在7：30之前到校的天数恰好多2”，求事件 $M$ 发生的概率.

5. 为了解甲、乙两种离子在小鼠体内的残留程度，进行如下试验：将200只小鼠随机分成A，B两组，每组100只，其中A组小鼠给服甲离子溶液，B组小鼠给服乙离子溶液，每只小鼠给服的溶液体积相同、摩尔浓度相同。经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图：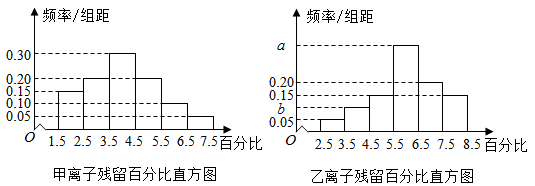

记C为事件：“乙离子残留在体内的百分比不低于5.5”，根据直方图得到P（C）的估计值为0.70.

6. 某行业主管部门为了解本行业中小企业的生产情况，随机调查了100个企业，得到这些企业第一季度相对于前一年第一季度产值增长率y的频数分布表。

y的分组	[-0.20，0)	[0，0.20)	[0.20，0.40)	[0.40，0.60)	[0.60，0.80)
企业数	2	24	53	14	7

附： $\sqrt{74}\approx 8.602$

7. 11分制乒乓球比赛，每赢一球得1分，当某局打成10：10平后，每球交换发球权，先多得2分的一方获胜，该局比赛结束.甲、乙两位同学进行单打比赛，假设甲发球时甲得分的概率为0.5，乙发球时甲得分的概率为0.4，各球的结果相互独立.在某局双方10：10平后，甲先发球，两人又打了X个球该局比赛结束.

8. 改革开放以来，人们的支付方式发生了巨大转变.近年来，移动支付已成为主要支付方式之一.为了解某校学生上个月A，B两种移动支付方式的使用情况，从全校所有的1000名学生中随机抽取了100人，发现样本中A，B两种支付方式都不使用的有5人，样本中仅使用A和仅使用B的学生的支付金额分布情况如下：

支付金额 支付方式	不大于2000元	大于2000元
仅使用A	27人	3人
仅使用B	24人	1人

（I）估计该校学生中上个月A，B两种支付方式都使用的人数；

（II）从样本仅使用B的学生中随机抽取1人，求该学生上个月支付金额大于2000元的概率；

（III）已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用B的学生中，随机抽查1人，发现他本月的支付金额大于2000元，结合（II）的结果，能否认为样本仅使用B的学生中本月支付金额大于2000元的人数有变化？说明理由.

9. 改革开放以来，人们的支付方式发生了巨大转变。近年来，移动支付已成为主要支付方式之一。为了解某校学生上个月A，B两种移动支付方式的使用情况，从全校学生中随机抽取了100人，发现样本中A，B两种支付方式都不使用的有5人，样本中仅使用A和仅使用B的学生的支付金额分布情况如下：

支付金额（元） 支付方式	（0，1000]	（1000，2000]	大于2000
仅使用A	18人	9人	3人
仅使用B	10人	14人	1人

（I）从全校学生中随机抽取1人，估计该学生上个月A，B两种支付方式都使用的概率；

（II）从样本仅使用A和仅使用B的学生中各随机抽取1人，以X表示这2人中上个月支付金额大于1000元的人数，求X的分布列和数学期望；

（III）已知上个月样本学生的支付方式在本月没有变化。现从样本仅使用A的学生中，随机抽查3人，发现他们本月的支付金额都大于2000元，根据抽查结果，能否认为样本仅使用A的学生中本月支付金额大于2000元的人数有变化？说明理由.

10. 某商场为提高服务质量，随机调查了50名男顾客和50名女顾客，每位顾客对该商场的服务给出满意或不满意的评价，得到下面列联表：

	满意	不满意
男顾客	40	10
女顾客	30	20

11. 为治疗某种疾病，研制了甲、乙两种新药，希望知道哪种新药更有效，为此进行动物试验。试验方案如下：每一轮选取两只白鼠对药效进行对比试验。对于两只白鼠，随机选一只施以甲药，另一只施以乙药。一轮的治疗结果得出后，再安排下一轮试验。当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时，就停止试验，并认为治愈只数多的药更有效。为了方便描述问题，约定：对于每轮试验，若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分，乙药得-1分：若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分，甲药得-1分：若都治愈或都未治愈则两种药均得0分。甲、乙两种药的治愈率分别记为α和β，一轮试验中甲药的得分记为X。