2019年高考数学真题分类汇编专题11：空间几何体（基础题）

试卷更新日期：2019-06-13 类型：二轮复习

进入出卷网下载

一、单选题

1. 设三棱锥V-ABC的底面是正三角形，侧棱长均相等，P是棱VA上的点，（不含端点），记直线PB与直线AC所成角为α.直线PB与平面ABC所成角为β.二面角P-AC-B的平面角为γ。则（）

A、β＜γ，a ＜γ B、β＜α，β＜γ C、β＜α，γ＜α D、α＜β ， γ＜β

查看试题解析
2. 设α，β为两个平面，则α∥β的充要条件是（）

A、α内有无数条直线与β平行 B、α内有两条相交直线与β平行 C、α，β平行于同一条直线 D、α，β垂直于同一平面

查看试题解析
3. 已知三棱锥P-ABC的四个顶点在球O的球面上，PA=PB=PC，∆ABC是边长为2的正三角形，E、F，分别是PA，AB的中点， $∠$ CEF=90°，则球O的体积为（）

A、 $8 \sqrt{6} π$ B、 $4 \sqrt{6} π$ C、 $2 \sqrt{6} π$ D、 $\sqrt{6} π$

查看试题解析
4. 祖暅是我国南北朝时代的伟大科学家，他提出的“幂势既同，则积不容异”称为祖暅原理，利用该原理可以得到柱体的体积公式V_柱体=sh，其中s是柱体的底面积，h是柱体的高。若某柱体的三视图如图所示，则该柱体的体积是（）

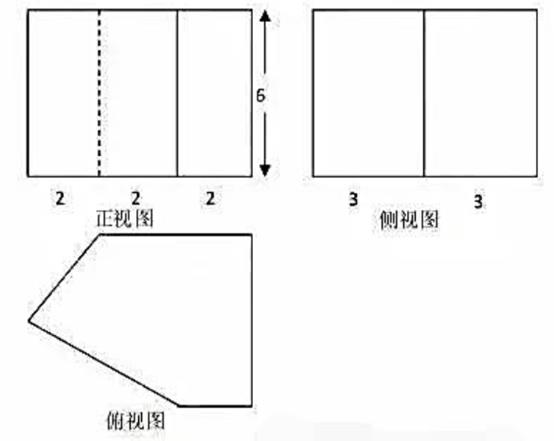A、158 B、162 C、182 D、32

查看试题解析
5. 如图，点N为正方形ABCD的中心，△ECD为正三角形，平面ECD⊥平面ABCD ， M是线段ED的中点，则（）

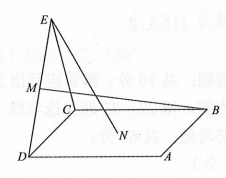A、BM=EN ，且直线BM、EN 是相交直线 B、BM≠EN ，且直线BM ， EN 是相交直线 C、BM=EN ，且直线BM、EN 是异面直线 D、BM≠EN ，且直线BM ， EN 是异面直线

查看试题解析

二、填空题

6. 如图，长方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的体积是120，E为 $C C_{1}$ 的中点，则三棱锥E-BCD的体积是.

查看试题解析
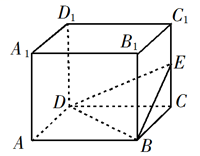7. 已知四棱锥的底面是边长为 $\sqrt{2}$ 的正方形，侧棱长均为 $\sqrt{5}$ .若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点，另一个底面的圆心为四棱锥底面的中心，则该圆柱的体积为.

查看试题解析
8. 学生到工厂劳动实践，利用3D打印技术制作模型，如图，该模型为长方体ABCD-A₁B₁C₁D₁ ，挖去四棱推O一EFGH后所得的几何体，其中O为长方体的中心，E，F，G，H，分别为所在棱的中点，AB=BC=6cm，AA₁=4cm，3D打印所用原料密度为0.9g/cm² ，不考虑打印损耗，制作该模型所需原料的质量为g.

查看试题解析
9. 中国有悠久的金石文化，印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体，但南北朝时期的官员独孤信的印信形状是“半正多面体”（图1）.半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体，它的所有顶点都在同一个正方体的表面上，且此正方体的棱长为1.则该半正多面体共有个面，其棱长为.

查看试题解析
10. 某几何体是由一个正方体去掉一个四棱柱所得.其三视图如图所示.如果网格纸上小正方形的边长为1.那么该几何体的体积为.

查看试题解析
11. 已知 $∠$ ACB=90°，P为平面ABC外一点，PC=2，点P到 $∠$ ACB两边AC，BC的距离均为 $\sqrt{3}$ ，那么P到平面ABC的距离为。

查看试题解析
12. 已知l，m是平面α外的两条不同直线.给出下列三个论断：
①l⊥m：②m∥α：③l⊥α.

以其中的两个论断作为条件，余下的一个论断作为结论，写出一个正确的命题：。

查看试题解析