山东省枣庄市2018-2019学年中考数学模拟考试试卷

试卷更新日期：2019-06-13 类型：中考模拟

进入出卷网下载

一、选择题：本大题共12小题，每小题选对得3分。

1. 2019的相反数是（）

A、 $\frac{1}{2019}$ B、2019 C、-2019 D、- $\frac{1}{2019}$

查看试题解析
2. 下列各运算中，计算正确的是（）

A、a¹²÷a³=a⁴ B、(3a²)³=9a⁶ C、(a-b)²=a²-ab+b² D、2a·3a=6a²

查看试题解析
3. 习近平总书记提出了未来五年“精准扶贫”的战略构想，意味着每年要减贫约11700000人，将数据11700000用科学记数法表示为（）

A、1.17×10⁷ B、1.7×10⁶ C、0.117×10⁷ D、1.17×10⁸

查看试题解析
4. 不等式组 ${\begin{cases} 2 x + 1 \geq - 3 \\ x < 1 \end{cases}$ 的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
5. 将一副直角三角板按如图所示的位置放置，使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边放在同一条直线上，则∠a的度数是（）

A、85° B、75° C、60° D、45°

查看试题解析
6. 某学习小组的五名同学在一次数学竞赛中的成绩分别是94分、98分、90分、94分、74分，则下列结论正确的是（）

A、平均分是91 B、中位数是90 C、众数是94 D、极差是20

查看试题解析
7. 新能源汽车环保节能，越来越受到消费者的喜爱。各种品牌相继投放市场。一汽贸公司经销某品牌新能源汽车．去年销售总额为5000万元，今年1~5月份，每辆车的销售价格比去年降低1万元。销售数量与去年一整年的相同．销售总额比去年一整年的少20%，今年1-5月份每辆车的销售价格是多少万元?设今年1-5月份每辆车的销售价格为x万元．根据题意，列方程正确的是（）

A、 $\frac{5000}{x + 1} = \frac{5000 (1 - 20 %)}{x}$ B、 $\frac{5000}{x + 1} = \frac{5000 (1 + 20 %)}{x}$ C、 $\frac{5000}{x - 1} = \frac{5000 (1 - 20 %)}{x}$ D、 $\frac{5000}{x - 1} = \frac{5000 (1 + 20 %)}{x}$

查看试题解析
8. 把图1中的正方体的一角切下后摆在图2所示的位置，则图2中的几何体的主视图为（）

A、 B、 C、 D、

查看试题解析
9. 如图，点A在线段BD上，在BD的同侧作等腰Rt△ABC和等腰Rt△ADE，CD与BE、AE分别交于点P，M．对于下列结论：①△BAE∽△CAD：②MP·MD=MA·ME：③2CB²=CP·CM．其中正确的是（）

A、①②③ B、① C、①② D、②③

查看试题解析
10. 甲、乙两车从A地出发，匀速驶向B地。甲车以80km/h的速度行驶1h后，乙车才沿相同路线行驶。乙车先到达B地并停留1h后，再以原速按原路返回，直至与甲车相遇．在此过程中，两车之间的距离y（km)与乙车行驶时间x（h)之间的函数关系如图所示。下列说法：①乙车的速度是120km/h；②m=160；③点H的坐标是（7，80）；@n-7.5．其中说法正确的是（）

A、①②③ B、①②④ C、①③④ D、①②③④

查看试题解析
11. 如图，在平面直角坐标系中，将正方形OABC绕点O逆时针旋转45°后得到正方形OA₁B₁C₁ ，依此方式，绕点O连续旋转2018次得到正方形OA₂₀₁₈B₂₀₁₈C₂₀₁₈ ，如果点A的坐标为（1，0），那么点B₂₀₁₈的坐标为（）

A、(1，1) B、(0， $\sqrt{2}$ ) C、（- $\sqrt{2}$ ，0） D、(-1，1)

查看试题解析
12. 如图，二次函数y=ax²+bx+c的图象经过点A（-1，0）、点B（3，0）、点C（4，1），若点D(x₂ ， y₂）是抛物线上任意一点，有下列结论：①二次函数y=ax²+bx+c的最小值为-4a；②若-1≤x2≤4，则0≤y₂≤5a；③若y₂>y₁ ，则x₂>4；④一元二次方程cx²+bx+a=0的两个根为-1和 $\frac{1}{3}$ 其中正确结论的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题：本题共6小题，每小题填对得4分，共24分。

13. 计算“2sin30°-（π- $\sqrt{2}$ ）⁰+| $\sqrt{3}$ -1|+（ $\frac{1}{2}$ ）^-1”的结果是 .

查看试题解析
14. 已知x，y满足方程组 ${\begin{cases} x - 2 y = 5 \\ x + 2 y = - 3 \end{cases}$ ,则x²-4y²的值为 .

查看试题解析
15. 如图，航拍无人机从A处测得一幢建筑物顶部B的仰角为45°，测得底部C的俯角为60°，此时航拍无人机与该建筑物的水平距离AD为110m，那么该建筑物的高度BC约为m（结果保留整数， $\sqrt{3}$ ≈1.73）

查看试题解析
16. 已知关于x的一元二次方程mx²+5x+m²-2m=0有一个根为0，则m=。

查看试题解析
17. 如图，在Rt△ABC中，∠ACB=90°，AC=BC=2，将Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE，点B经过的路径为弧BD，则图中阴影部分的面积为．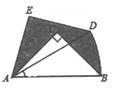

查看试题解析
18. 如图，点A（0，1），点B（- $\sqrt{3}$ ，0），作OA₁⊥AB，垂足为A，以OA₁为边做Rt△A₁OB₁ ，使∠A₁OB₁=90°，使∠B₁=30；作OA₂⊥A₁B₁ ，垂足为A₂ ，再以OA₂为边作Rt△A₂OB₂ ，使∠A₂OB₂=90°，∠B₂=30°，…，以同样的作法可得到Rt△A_nOB_n ．则当n=2018时，点B₂₀₁₈纵坐标为．

查看试题解析

三、解答题：本题共7小题，满分60分。

19. 先化简，再求值： $\frac{8}{x^{2} - 4 x + 4}$ ÷( $\frac{x^{2}}{x - 2}$ -x-2)，其中|x|=2．

查看试题解析
20. 如图，△ABC在平面直角坐标系内，顶点的坐标分别为A（-4，4），B（-2，5），C（-2，1）．

(1)、平移△ABC，使点C移到点C₁（-2，-4），画出平移后的△A₁B₁C₁ ，并写出点A₁ ， B₁的坐标；

(2)、将△ABC绕点（0，3)旋转180°，得到△A₂B₂C₂ ，画出旋转后的△A₂B₂C₂；

(3)、求（2）中的点C旋转到点C₂时，点C经过的路径长（结果保留π）．

查看试题解析
21. 某电视台为了解本地区电视节目的收视情况，对部分市民开展了“你最喜爱的电视节目”的问卷调查（每人只填写一项），根据收集的数据绘制了两幅不完整的统计图（如图所示），根据要求回答下列问题：

(1)、本次问卷调查共调查了名观众；图②中最喜爱“新闻节目”的人数占调查总人数的百分比为；

(2)、补全图①中的条形统计图；

(3)、现有最喜爱“新闻节目”（记为A），、“体育节目”（记为B），“综艺节目”（记为C），“科普节目”（记为D）的观众各一名，电视台要从四人中随机抽取两人参加联谊活动，请用列表或画树状图的方法，求出恰好抽到最喜爱“B”和“C”两位观众的概率。

查看试题解析
22. 如图，在△ABC中，AD是BC边上的中线，E是AD的中点，过点A作BC的平行线交BE的延长线于点F，连接CF．

(1)、求证：AF=DC；

(2)、若ABLAC，试判断四边形ADCF的形状，并证明你的结论．

查看试题解析
23. 如图，在平面直角坐标系中，直线y=- $\frac{1}{2}$ x与反比例函数y= $\frac{k}{x}$ （k#0）在第二象限内的图象相交于点A（m，1）．

(1)、求反比例函数的解析式；

(2)、将直线y=- $\frac{1}{2}$ x向上平移后与反比例函数图象在个第二象限内交于点B，与y轴交于点C，且△ABO的面积为 $\frac{3}{2}$ ，求直线BC的解析式。

查看试题解析
24. 如图，以△ABC的边AB为直径画⊙O，交AC于点D，半径OE∥BD，连接BE，DE，BD，设BE交AC于点F，若∠DEB=∠DBC．

(1)、求证：BC是⊙O的切线；

(2)、若BF=BC=2，求图中阴影部分的面积。

查看试题解析
25. 如图，已知抛物线经过点A（-1，0），B（4，Q），C（0，2)三点，点D与点C关于x轴对称，点P是x轴上的一个动点，设点P的坐标为（m，0)，过点P做x轴的垂线l交抛物线于点Q，交直线于点M．

(1)、求该抛物线所表示的二次函数的表达式；

(2)、已知点F（0， $\frac{1}{2}$ ），当点P在x轴上运动时，试求m为何值时，四边形DMQF是平行四边形?

(3)、点P在线段AB运动过程中，是否存在点Q，使得以点B、Q、M为顶点的三角形与△BOD相似?若存在，求出点Q的坐标；若不存在，请说明理由．

查看试题解析