山东省泰安市高新区2018-2019学年中考数学二模考试试卷
试卷更新日期:2019-06-13 类型:中考模拟
一、选择题(本大题共12个小题,每小题选对4分。)
-
1. -5的相反数是( )A、-5 B、5 C、0 D、2. 计算:(a2)3-5a4·a2的结果是( )A、a5-5a6 B、a6-5a8 C、-4a6 D、4a63. 从下列4个图形中任选一个,得到的图形既是轴对称图形又是中心对称图形的概率是( )
 A、 B、 C、 D、14. “2014年至2016年,中国同一带一路沿线国家贸易总额超过32.1万亿美元”,将数据32.1万亿美元用科学记数法表示( )A、3.21×1014美元 B、32.1×1012美元 C、3.21×1013美元 D、3.21×1011美元5. 将一副三角板按如图的方式进行摆放,则∠ 的度数是( )
A、 B、 C、 D、14. “2014年至2016年,中国同一带一路沿线国家贸易总额超过32.1万亿美元”,将数据32.1万亿美元用科学记数法表示( )A、3.21×1014美元 B、32.1×1012美元 C、3.21×1013美元 D、3.21×1011美元5. 将一副三角板按如图的方式进行摆放,则∠ 的度数是( ) A、45° B、60° C、75° D、105°6. 以下是某初中九年级10名学生参加托球测试成绩
A、45° B、60° C、75° D、105°6. 以下是某初中九年级10名学生参加托球测试成绩成绩/个
35
40
45
60
70
人数/人
1
2
4
2
1
则这组数据的中位数、平均数分别是( )
A、45,49 B、45,48.5 C、55,50 D、60,517. 如图,将边长为4的正△ABC沿EF折叠,使A点落在边BC上G点,且BG=1,CF=( )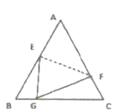 A、 B、 C、 D、8. 如图,AB为⊙O的直径,CD是⊙O的弦,∠ADC=35°,则∠CAB的度数为( )
A、 B、 C、 D、8. 如图,AB为⊙O的直径,CD是⊙O的弦,∠ADC=35°,则∠CAB的度数为( )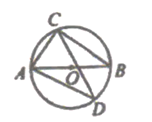 A、35° B、45° C、55° D、65°9. 抛物线y=ax2+bx+c的图象如图所示,则一次函数y=ax+b与反比例函数y= 在同一平面直角坐标系内的图象大致为( )
A、35° B、45° C、55° D、65°9. 抛物线y=ax2+bx+c的图象如图所示,则一次函数y=ax+b与反比例函数y= 在同一平面直角坐标系内的图象大致为( ) A、
A、 B、
B、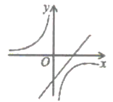 C、
C、 D、
D、 10. 如图,四边形ABCD为平行四边形,E、F为CD边的两个三等分点,连接AF、BE交于点G,则S△EFG:S△ABG=( )
10. 如图,四边形ABCD为平行四边形,E、F为CD边的两个三等分点,连接AF、BE交于点G,则S△EFG:S△ABG=( )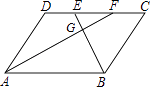 A、1:3 B、3:1 C、1:9 D、9:111. 抛物线y=ax2+bxtc的对称轴为直线x=1,与y轴的交点为C,与x轴交于点A,点B(-2,0),则①2a+b=0②c-4b>0③当m≠1,a+b>am2+bm④点D为抛物线上的点,当△ABD为等腰直角三角形时a=- ⑤b2-4ac>0其中正确答案的序号是( )
A、1:3 B、3:1 C、1:9 D、9:111. 抛物线y=ax2+bxtc的对称轴为直线x=1,与y轴的交点为C,与x轴交于点A,点B(-2,0),则①2a+b=0②c-4b>0③当m≠1,a+b>am2+bm④点D为抛物线上的点,当△ABD为等腰直角三角形时a=- ⑤b2-4ac>0其中正确答案的序号是( ) A、①②③④ B、①③④⑤ C、②③④⑤ D、①②④⑤
A、①②③④ B、①③④⑤ C、②③④⑤ D、①②④⑤二、填空题(本大题共6小题,满分24分.每小题填对得4分)
-
12. 分解因式:2x4-2= .13. 为测量某物体AB的高度,在点D测得A的仰角为45°,朝物体AB方向前进40m,到达C,再次测得点A的仰角为60°,则物体AB的高度为m.
 14. 如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则OF的长度是cm.
14. 如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则OF的长度是cm. 15. 如图,单位网格中,将线段AB先向右平移2个单位,再向上平移2个单位,然后再绕P点按顺时针方向旋转90°得到A'B',则A的坐标是
15. 如图,单位网格中,将线段AB先向右平移2个单位,再向上平移2个单位,然后再绕P点按顺时针方向旋转90°得到A'B',则A的坐标是 16. 如图,在△ABC中,点D是边AB上的一点,∠ADC=∠ACB,AD=4,BD=5,则边AC的长为 .
16. 如图,在△ABC中,点D是边AB上的一点,∠ADC=∠ACB,AD=4,BD=5,则边AC的长为 . 17. 如图,直线y=x,点A1坐标为(1,0),过点Aa作x轴的垂线交直线于点B1 , 以原点0为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2 , 以原点0为圆心,OB2长为半径画弧交x轴于点A3…,按照此做法进行下去,则OA2019的长为 .
17. 如图,直线y=x,点A1坐标为(1,0),过点Aa作x轴的垂线交直线于点B1 , 以原点0为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2 , 以原点0为圆心,OB2长为半径画弧交x轴于点A3…,按照此做法进行下去,则OA2019的长为 .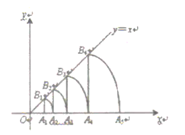
三、解答题(本大题共7小题,满分78分.)
-
18. 先化简,再求值:
其中x= ,y=2cos45°-
19. 我校九年级一班组织读书月活动,班委会对学生读的书籍进行调查问卷,问卷设置了“小说”“散文”“诗歌”“其他”四个类型,每个同学只选一项,根据调查结果制作的频数分布表和扇形统计图。类别
频数(人数)
频率
小说
0.4
诗歌
5
散文
其他
8
0.16
总计
1
 (1)、补全频数分布表,并求出扇形统计图的百分比.(2)、若全校九年学生有500名,则估测全校九年级学生喜爱读小说的有几人?(3)、现有ABCD四名学生,在其选出2名学生参加诗歌演讲,请用画树状图或列表法的方法,求恰好抽中A和B的概率。20. 如图,在平面直角坐标系中,一次函数y1=kx+b(k≠0)与反比例函数y2= (m≠0)的图象交于第二、第四象限A,B两点,过点A作AD⊥x轴,垂足为D,AD=4,sin∠AOD= ,且点B的坐标为(n,2)
(1)、补全频数分布表,并求出扇形统计图的百分比.(2)、若全校九年学生有500名,则估测全校九年级学生喜爱读小说的有几人?(3)、现有ABCD四名学生,在其选出2名学生参加诗歌演讲,请用画树状图或列表法的方法,求恰好抽中A和B的概率。20. 如图,在平面直角坐标系中,一次函数y1=kx+b(k≠0)与反比例函数y2= (m≠0)的图象交于第二、第四象限A,B两点,过点A作AD⊥x轴,垂足为D,AD=4,sin∠AOD= ,且点B的坐标为(n,2) (1)、求一次函数与反比例函数的表达式;(2)、将一次函数y1=kx+b((k≠0)向上移动2个单位的函数记为y3 , 当y3<y2时,求x的取值范围;(3)、若函数y3为与函数y2 , 在第二象限交于点E,连接BE、AE,求△ABE的面积.21. 某服装商预测一种应季衬衫能畅销市场,用8000元购进一批此种衬衫,面市后果然供不应求,服装商又用17600元购进了第二批这种衬衫,所购数量是第一批购进数量的2倍,但单价贵了8元.商家销售这种衬衫时每件定价为100元,最后10件按8折销售,很快售完.(1)、两批进货的单价各是多少元?(2)、在这两笔生意中,商家共盈利多少元?22. 如图:抛物线y=- x2+bx+c与y轴交于点c(0,4),与x轴交于A、B两点,且B点坐标为(4,0)
(1)、求一次函数与反比例函数的表达式;(2)、将一次函数y1=kx+b((k≠0)向上移动2个单位的函数记为y3 , 当y3<y2时,求x的取值范围;(3)、若函数y3为与函数y2 , 在第二象限交于点E,连接BE、AE,求△ABE的面积.21. 某服装商预测一种应季衬衫能畅销市场,用8000元购进一批此种衬衫,面市后果然供不应求,服装商又用17600元购进了第二批这种衬衫,所购数量是第一批购进数量的2倍,但单价贵了8元.商家销售这种衬衫时每件定价为100元,最后10件按8折销售,很快售完.(1)、两批进货的单价各是多少元?(2)、在这两笔生意中,商家共盈利多少元?22. 如图:抛物线y=- x2+bx+c与y轴交于点c(0,4),与x轴交于A、B两点,且B点坐标为(4,0)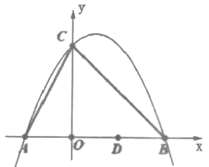 (1)、求该抛物线的解析式;(2)、若P是线段BC上的一个动点,当P在何处时,四边形ACPB面积最大,并求最大面积;(3)、若Q为AB上的一个动点,过Q做QM∥AC,当Q在何处时,△QCM的面积最大?(4)、若点D为OB的中点,E为BC上的动点,当△OED为等腰三角形时,求E点坐标。23. 以四边形ABCD的边AB、AD为边分别向外侧作等腰三角形ABF和ADE.
(1)、求该抛物线的解析式;(2)、若P是线段BC上的一个动点,当P在何处时,四边形ACPB面积最大,并求最大面积;(3)、若Q为AB上的一个动点,过Q做QM∥AC,当Q在何处时,△QCM的面积最大?(4)、若点D为OB的中点,E为BC上的动点,当△OED为等腰三角形时,求E点坐标。23. 以四边形ABCD的边AB、AD为边分别向外侧作等腰三角形ABF和ADE. (1)、当四边形ABCD为正方形时(如图1),以边AB、AD为斜边分别向外侧作等腰直角三角形ABF和ADE,连接EB、FD,线段EB和FD的数量关系是 ;(2)、当四边形ABCD为矩形时(如图2),以边AB、AD为斜边分别向矩形内侧、外侧作等腰直角三角形ABF和ADE,连接EB、FD,线段EF和BD具有怎样的数量关系?请说明理由;(3)、四边形ABCD为平行四边形时,以边AB、AD为斜边分别向平行四边形内侧、外侧作等腰三角形ABF和ADE,且△EAD与△FBA的顶角都为a,连接EF、BD,交点为G.请用a表示出∠EGD,并说明理由。
(1)、当四边形ABCD为正方形时(如图1),以边AB、AD为斜边分别向外侧作等腰直角三角形ABF和ADE,连接EB、FD,线段EB和FD的数量关系是 ;(2)、当四边形ABCD为矩形时(如图2),以边AB、AD为斜边分别向矩形内侧、外侧作等腰直角三角形ABF和ADE,连接EB、FD,线段EF和BD具有怎样的数量关系?请说明理由;(3)、四边形ABCD为平行四边形时,以边AB、AD为斜边分别向平行四边形内侧、外侧作等腰三角形ABF和ADE,且△EAD与△FBA的顶角都为a,连接EF、BD,交点为G.请用a表示出∠EGD,并说明理由。