山东省滨州市沾化县2018-2019学年中考数学一模考试试卷
试卷更新日期:2019-06-13 类型:中考模拟
一、选择题:本大题共12个小题,每小题3分,满分36分.
-
1. -的相反数是( )A、- B、 C、- D、2. 下列“数字图形”中,既是轴对称图形,又是中心对称图形的有( )
 A、1个 B、2个 C、3个 D、4个3. 将0.000102用科学记数法表示为( )A、1.02×10-4 B、1.02×10-5 C、1.02×10-6 D、102×10-34. 如图,已知AB∥DE,∠ABC=75°,∠CDE=145°,则∠BCD的值为( )
A、1个 B、2个 C、3个 D、4个3. 将0.000102用科学记数法表示为( )A、1.02×10-4 B、1.02×10-5 C、1.02×10-6 D、102×10-34. 如图,已知AB∥DE,∠ABC=75°,∠CDE=145°,则∠BCD的值为( )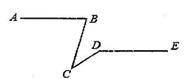 A、20° B、30° C、40° D、70°5. 已知∠BAC=45°,一动点O在射线AB上运动(点O与点A不重合),设OA=x,如果半径为1的⊙O与射线AC有公共点,那么x的取值范围是( )A、0<x≤1 B、1≤x< C、0<x≤ D、x>6. 如图,△ABC中,AB>AC,∠CAD为△ABC的外角,观察图中尺规作图的痕迹,则下列结论错误的是( )
A、20° B、30° C、40° D、70°5. 已知∠BAC=45°,一动点O在射线AB上运动(点O与点A不重合),设OA=x,如果半径为1的⊙O与射线AC有公共点,那么x的取值范围是( )A、0<x≤1 B、1≤x< C、0<x≤ D、x>6. 如图,△ABC中,AB>AC,∠CAD为△ABC的外角,观察图中尺规作图的痕迹,则下列结论错误的是( )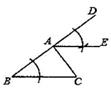 A、∠DAE=∠B B、∠EAC=∠C C、∠DAE=∠EAC D、AE∥BC7. 如图,数轴上A,B两点所表示的数互为倒数,则关于原点的说法正确的是( )
A、∠DAE=∠B B、∠EAC=∠C C、∠DAE=∠EAC D、AE∥BC7. 如图,数轴上A,B两点所表示的数互为倒数,则关于原点的说法正确的是( ) A、一定在点A的左侧 B、一定与线段AB的中点重合 C、可能在点B的右侧 D、一定与点A或点B重合8. 下列运算中正确的是( )A、x4·x=x5 B、2x3÷ x=4x4 C、(-a2)4=a6 D、5x-3x=29. 下列说法中正确的是( )A、“打开电视,正在播放新闻节目”是必然事件 B、“抛一枚硬币,正面向上的概率为 ”表示每抛两次就有一次正面朝上 C、“抛一枚均匀的正方体骰子,朝上的点数是6的概率为 ”表示随着抛掷次数的增加,“抛出朝上的点数是6”这一事件发生的频率稳定在 附近 D、为了解某种节能灯的使用寿命,选择全面调查10. 已知点A(x1 , y1),(x2 , y2)是反比例函数y= 图象上的点,若x1>0>x2 , 则一定成立的是( )A、y1>y2>0 B、y1>0>y2 C、0>y1>y2 D、y2>0>y111. 小明坐滴滴打车前去火车高铁站,小明可以选择两条不同路线:路线A的全程是25千米,但交通比较拥堵,路线B的全程比路线A的全程多7千米,但平均车速比走路线A时能提高60%,若走路线B的全程能比走路线A少用15分钟.若设走路线A时的平均速度为x千米/小时,根据题意,可列分式方程( )
A、一定在点A的左侧 B、一定与线段AB的中点重合 C、可能在点B的右侧 D、一定与点A或点B重合8. 下列运算中正确的是( )A、x4·x=x5 B、2x3÷ x=4x4 C、(-a2)4=a6 D、5x-3x=29. 下列说法中正确的是( )A、“打开电视,正在播放新闻节目”是必然事件 B、“抛一枚硬币,正面向上的概率为 ”表示每抛两次就有一次正面朝上 C、“抛一枚均匀的正方体骰子,朝上的点数是6的概率为 ”表示随着抛掷次数的增加,“抛出朝上的点数是6”这一事件发生的频率稳定在 附近 D、为了解某种节能灯的使用寿命,选择全面调查10. 已知点A(x1 , y1),(x2 , y2)是反比例函数y= 图象上的点,若x1>0>x2 , 则一定成立的是( )A、y1>y2>0 B、y1>0>y2 C、0>y1>y2 D、y2>0>y111. 小明坐滴滴打车前去火车高铁站,小明可以选择两条不同路线:路线A的全程是25千米,但交通比较拥堵,路线B的全程比路线A的全程多7千米,但平均车速比走路线A时能提高60%,若走路线B的全程能比走路线A少用15分钟.若设走路线A时的平均速度为x千米/小时,根据题意,可列分式方程( )
A、 =15 B、 =15 C、 = D、 =12. 如图,在等边三角形ABC中,AB=2,动点P从点A出发,沿三角形边界按顺时针方向匀速运动一周,点Q在线段AB上,且满足AQ+AP=2.设点P运动的时间为x,AQ的长为y,则y与x的函数图象大致是( )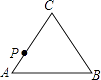 A、
A、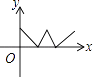 B、
B、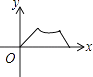 C、
C、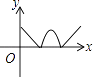 D、
D、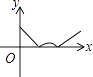
二、填空题:本大题共8个小题,每小题5分,满分40分.
-
13. (-3)2的平方根等于 .14. 若a,b为实数,且|a+1|+ =0,则(ab)2019的值是 .15. 将一个二次三项式分解因式,一位同学因看错了一次项系数而分解成3(x-1)(x-9),另一位同学因看错了常数项而分解成3(x-2)(x-4),那么这个二次三项式正确的分解应是 .16. 从3、1、-2这三个数中任取两个不同的数作为P点的坐标,则P点刚好落在第四象限的概率是 .17. 如图是由若干个大小相同的小正方体所搭成的几何体的三视图,则搭成这个几何体的小正方体的个数是个.
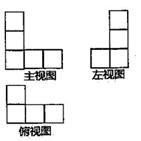 18. 如图,直线m∥n,以直线m上的点A为圆心,适当长为半径画弧,分别交直线m,n于点B、C,连接AC、BC,若∠1=30°,则∠2= .
18. 如图,直线m∥n,以直线m上的点A为圆心,适当长为半径画弧,分别交直线m,n于点B、C,连接AC、BC,若∠1=30°,则∠2= .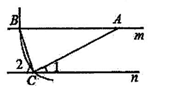 19. 如图,点E在 ABCD的边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD上的点F,若△FDE的周长为29,△FCB的周长为51,则FC= .
19. 如图,点E在 ABCD的边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD上的点F,若△FDE的周长为29,△FCB的周长为51,则FC= . 20. 如图,某点从数轴上的A点出发,第1次向右移动1个单位长度至B点,第2次从B点向左移动2个单位长度至C点,第3次从C点向右移动3个单位长度至D点,第4次从D点向左移动4个单位长度至E点,…,依此类推,经过次移动后该点到原点的距离为2018个单位长度。
20. 如图,某点从数轴上的A点出发,第1次向右移动1个单位长度至B点,第2次从B点向左移动2个单位长度至C点,第3次从C点向右移动3个单位长度至D点,第4次从D点向左移动4个单位长度至E点,…,依此类推,经过次移动后该点到原点的距离为2018个单位长度。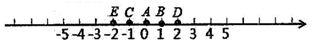
三、解答题:本大题共6个小题,满分74分.
-
21. 现要在△ABC的边AC上确定一点D,使得点D到AB,BC的距离相等.
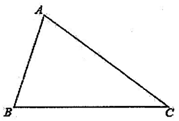 (1)、如图,请按要求在图上出作点D(尺规作图,不写作法,保留作图痕迹);(2)、若AB=4,BC=6,△ABC的面积为12,求点D到AB的距离。22. “雪龙”号考察船在某海域进行科考活动,在点A处测得小岛C在它的东北方向上,它沿南偏东37°方向航行2海里到达点B处,又测得小岛C在它的北偏东23°方向上(如图所示),求“雪龙”号考察船在点B处与小岛C之间的距离.
(1)、如图,请按要求在图上出作点D(尺规作图,不写作法,保留作图痕迹);(2)、若AB=4,BC=6,△ABC的面积为12,求点D到AB的距离。22. “雪龙”号考察船在某海域进行科考活动,在点A处测得小岛C在它的东北方向上,它沿南偏东37°方向航行2海里到达点B处,又测得小岛C在它的北偏东23°方向上(如图所示),求“雪龙”号考察船在点B处与小岛C之间的距离.(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40, ≈1.4, ≈1.7)
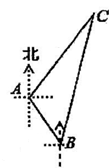 23. 如图,四边形ABCD是以坐标原点O为对称中心的矩形,4(1,3),B(-3,-1),该矩形的边与坐标轴分别交于点E、F、G、H,连接EC.
23. 如图,四边形ABCD是以坐标原点O为对称中心的矩形,4(1,3),B(-3,-1),该矩形的边与坐标轴分别交于点E、F、G、H,连接EC.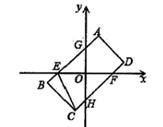 (1)、求四边形ECHO的面积;(2)、如果反比例函数的图象过点A,那么它是否一定过点D?请说明理由24. 学校为开展“阳光体育”活动,需要购买一批篮球、足球和排球,已知每10人需要购买一个篮球,每12人需要购买一个排球,每20人需要购买一个足球.李老师根据调查,将统计的参加各项活动的学生人数的结果绘制成了下列尚不完整的统计图.
(1)、求四边形ECHO的面积;(2)、如果反比例函数的图象过点A,那么它是否一定过点D?请说明理由24. 学校为开展“阳光体育”活动,需要购买一批篮球、足球和排球,已知每10人需要购买一个篮球,每12人需要购买一个排球,每20人需要购买一个足球.李老师根据调查,将统计的参加各项活动的学生人数的结果绘制成了下列尚不完整的统计图.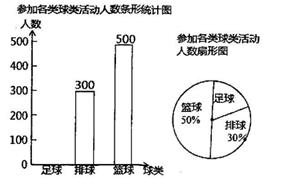 (1)、求参加足球活动的学生人数,并将条形统计图补充完整;(2)、已知一个足球比一个篮球的价格高30元,一个排球的价格是一个篮球价格的 买3个篮球、1个足球、2个排球一共需要478元.
(1)、求参加足球活动的学生人数,并将条形统计图补充完整;(2)、已知一个足球比一个篮球的价格高30元,一个排球的价格是一个篮球价格的 买3个篮球、1个足球、2个排球一共需要478元.①求篮球、足球和排球的单价;
②根据实际需要,学校决定购买篮球52个,足球和排球共48个,请求出购买资金W与购买足球个数m之间的函数解析式。若足球购买的数量不少于篮球数量的 ,学校准备8000元的购买资金能满足要求吗?请说明理由.
25. 如图①,已知AB是⊙O的直径,点D是线段AB延长线上的一个动点,直线DF垂直于射线AB于点D,当直线DF绕点D逆时针旋转时,与⊙O交于点C,且运动过程中,保持CD=OA.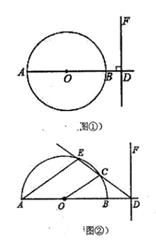 (1)、当直线DF与⊙O相切于点C时,求旋转角的度数;(2)、当直线DF与半圆O相交于点C时(如图②),设另一交点为E,连接AE,OC,若AE∥OC.
(1)、当直线DF与⊙O相切于点C时,求旋转角的度数;(2)、当直线DF与半圆O相交于点C时(如图②),设另一交点为E,连接AE,OC,若AE∥OC.①求AE与OD的大小有什么关系?说明理由:
②求此时旋转角的度数.
26. 如图,已知抛物线与x轴交于A、B两点,与y轴交于C点,对称轴为直线x=1,且A(-1,0),C(0,3).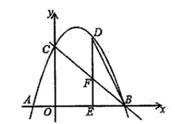 (1)、求该抛物线的解析式;(2)、点D是第一象限内抛物线上的一个动点(与点C、B不重合),过点D作DE⊥x轴于点E,交直线BC于点F,连接BD,设点D的横坐标为m,△BEF的面积为S.求S关于m的函数关系式并直接写出自变量m的取值范围;(3)、直线BC能否把△BDE分成面积之比为2:3的两部分?若能,请求出点D的坐标;若不能,请说明理由.
(1)、求该抛物线的解析式;(2)、点D是第一象限内抛物线上的一个动点(与点C、B不重合),过点D作DE⊥x轴于点E,交直线BC于点F,连接BD,设点D的横坐标为m,△BEF的面积为S.求S关于m的函数关系式并直接写出自变量m的取值范围;(3)、直线BC能否把△BDE分成面积之比为2:3的两部分?若能,请求出点D的坐标;若不能,请说明理由.