黑龙江省哈尔滨市松北区2017-2018学年七年级下学期数学期末考试试卷

试卷更新日期：2019-06-13 类型：期末考试

进入出卷网下载

一、单选题

1. 下列方程中是二元一次方程的是（）

A、2 x ² - 4 = 0 B、xy = 3 C、2x + $\frac{y}{2}$ = 1 D、x + $\frac{1}{y}$ = 3

查看试题解析
2. 若m＜n，则下列各式正确的是（）

A、2m＞2n B、m﹣2＞n﹣2 C、﹣3m＞﹣3n D、 $\frac{π}{3}$ ＞ $\frac{n}{3}$

查看试题解析
3. 以下列各组线段为边，能构成三角形的是（）

A、2，3，6 B、3，4，5 C、2，7，9 D、 $\frac{3}{2}$ ，3， $\frac{3}{2}$

查看试题解析
4. 已知 ${\begin{matrix} x = 1 \\ y = 2 \end{matrix}$ 是方程 ax-y=3 的一个解，那么 a 的值为（）

A、-4 B、4 C、-5 D、5

查看试题解析
5. 甲、乙两台机床生产一种零件，在 10 天中两台机床每天生产的次品数的平均数是 $\bar{x_{甲}} =$ $\bar{x_{乙}} =2$ ，方差是 $S_{甲}^{2} = 1.65$ ， $S_{乙}^{2} =0 .76$ 出次品的波动较小的是（）台机床

A、甲 B、乙 C、甲、乙一样 D、不能确定

查看试题解析
6. 若一个多边形的内角和为 540°，那么这个多边形对角线的条数为（）

A、5 B、6 C、7 D、8

查看试题解析
7. 如图，△ACB≌△A' CB'，∠BCB'=30°，则∠ACA'的度数为（）

A、20° B、30° C、35° D、40°

查看试题解析
8. 在直角坐标系中，点P(2x-6，x-5)在第四象限，则x的取值范围是（）

A、3<x<5 B、-3<x<5 C、-5<x<3 D、-5<x<-3

查看试题解析
9. 如图，已知点 D是∠ABC的平分线上一点，点 P在 BD上，PA⊥AB，PC⊥BC，垂足分别为 A，C．下列结论错误的是（）

A、∠ADB=∠CDB B、△ABP≌△CBP C、△ABD ≌△CBD D、AD=CP

查看试题解析
10. 下列说法中：①三角形中至少有2个角是锐角；②各边都相等的多边形是正多边形；③钝角三角形的三条高交于一点；④两个等边三角形全等；⑤三角形两个内角的平分线的交点到三角形三边的距离相等，正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 已知 4x-y =5，用 x 表示 y，得 y= ．

查看试题解析
12. x的 $\frac{1}{2}$ 与5的差不小于3，用不等式表示为．

查看试题解析
13. 已知△ABC 的两条边长分别为 5 和 8，那么第三边长 x 的取值范围-.

查看试题解析
14. 某校七年级（1）班 7 名女同学的体重（单位：kg）分别是：53、40、42、42、35、36、45 这组数据的中位数是

查看试题解析
15. 如图，在△ABC 中，∠A=60°，D 是 AB 上一点，E 是 AC 上一点，BE、CD 相交于 O，且∠BOD=55°，∠ACD=30°，则∠ABE 的度数是.

查看试题解析
16. 若不等式3x-m≤0的正整数解恰好是1、2、3，则m的取值范围是.

查看试题解析
17. 等腰三角形周长为 24，其中一条边长为 6，则一个腰长是- .

查看试题解析
18. 幼儿园把新购进的一批玩具分给小朋友．如果每人 5 件，那么还剩余 12 件；如果每人 8 件，那么最后一个小朋友分到玩具，但不足 4 件，这批玩具共有件.

查看试题解析
19. 在平面直角坐标系中，点 O为坐标原点，A（4，3），B（4，0），在坐标轴上有一点C，使得△AOB 与△COB 全等，则 C 点坐标为.

查看试题解析
20. 如图，在四边形 ABCD 中，AC 是对角线，AB=CD，∠DAC+∠BCA=180°，∠BAC+∠ACD=90°，四边形 ABCD 的面积是 18，则 CD 的长是.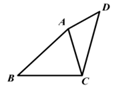

查看试题解析

三、解答题

21. 解二元一次方程组.：

(1)、 ${\begin{matrix} 3 x + 2 y = 7 \\ 4 x - y = 13 \end{matrix}$ ；

(2)、 ${\begin{matrix} \frac{x}{4} - y = - 1 \\ 3 (x - y) = 2 x \end{matrix}$

查看试题解析
22. 解下列不等式和不等式组，并用数轴表示解集.

(1)、 $10 - 4 (x - 3) \leq 2 (x - 1)$ ；(2) ${\begin{matrix} x - 3 (x - 2) < 0 \\ \frac{1 + 2 x}{3} \geq x - 1 \end{matrix}$

查看试题解析
23. 如图，在 5×5 的方格纸中，我们把像△ABC 这样的三个顶点都在网格的格点上的三角形叫做格点三角形．

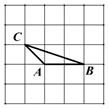(1)、试在如图①方格纸上画出与△ABC 只有一个公共顶点 C 且全等的格点三角形（只画一个）；

(2)、试在如图②方格纸上画出与△ABC 只有一个公共边 AB 且全等的格点三角形（只画一个）．

查看试题解析
24. 为了调查学生每天零花钱情况，对我校初二学年某班 50 名同学每天零花钱情况进行了统计，并绘制成下面的统计图．

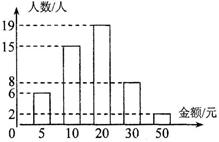(1)、直接写出这 50 名同学零花钱数据的众数是；中位数是．

(2)、求这 50 名同学零花钱的平均数．

(3)、该校共有学生 3100 人，请你根据该班的零花钱情况，估计这个中学学生每天的零花钱不小于 30 元的人数．

查看试题解析
25. 某商店购进甲、乙两种商品，购进 4 件甲种商品比购进 5 件乙种商品少用 10 元，购进 20 件甲种商品和 10 件乙种商品共用去 160 元.

(1)、求甲、乙两种商品每件进价分别是多少元？

(2)、若该商店购进甲、乙两种商品共 140 件，都标价 10 元出售，售出一部分降价促销，以标价的八折售完所有剩余商品，以 10 元售出的商品件数比购进甲种商品件数少 20 件，该商店此次购进甲、乙两种商品降价前后共获利不少于 420 元，求至少购进甲种商品多少件？

查看试题解析
26. 在△ABC 中，∠ACB=90° AD 是它的角平分线，EB⊥AB 于点 B 且交 AD 的延长线于点 E.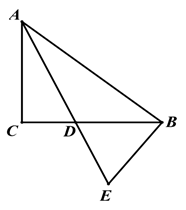

图 1 图 2

(1)、如图 1，求证：BD=BE

(2)、如图 2，过点 E 作 EF⊥BC 于点 F， CF：BF=5：3， BE=10，求 DF 的长.

查看试题解析
27. 在平面直角坐标系中，点 A(2，0)，B(0，4)，点 C 在第一象限.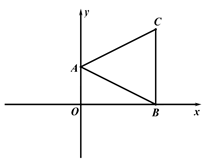

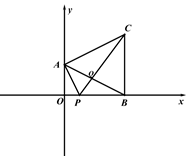
图 1 图 2

(1)、如图 1，连接 AB、BC、AC，∠OBC=90°，∠BAC=2∠ABO，求点 C 的坐标；

(2)、动点 P 从点 B 出发，以每秒 2 个单位的速度沿 x 轴负方向运动，连接 AP，设 P 点的运动时间为 t 秒，△AOP 的面积为 S，用含 t 的式子表示 S，并直接写出 t 的取值范围；

(3)、如图 2，在（1）条件下，点 P 在线段 OB 上，连接 AP、PC，AB 与 PC 相交于点 Q，当S=3， ∠BAC=∠BPC 时，求△ACQ 的面积.

查看试题解析