广东省深圳市福田区2017-2018学年七年级下学期数学期末考试试卷

试卷更新日期：2019-06-13 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列运算正确的是（）

A、 $a^{2} \cdot a^{3} = a^{5}$ B、 $a^{6} \cdot a^{3} = a^{18}$ C、 ${(a^{3})}^{2} = a^{5}$ D、 $a^{5} + a^{5} = a^{10}$

查看试题解析
3. 有下列长度的三条线段，能组成三角形的是（）

A、2cm，3cm，4cm B、1cm，4cm，2cm C、1cm，2cm，3cm D、6cm，2cm，3cm

查看试题解析
4. 空气的密度是 0.001293g/ $c m^{3}$ ，0.001293 用科学记数法表示为（）

A、1.293× $10^{3}$ B、1.293× $10^{- 3}$ C、1.293× $10^{- 4}$ D、12.93× $10^{- 4}$

查看试题解析
5. 下列事件中，随机事件是（）

A、. 经过有交通信号灯的路口，遇到红灯 B、实心铁球投入水中会沉入水底 C、一滴花生油滴入水中，油会浮在水面 D、两负数的和为正数

查看试题解析
6. 如图，直线AB∥CD，则下列结论正确的是（）

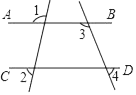A、∠1=∠2 B、∠3=∠4 C、∠1+∠3=180° D、∠3+∠4=180°

查看试题解析
7. 下列各题中，适合用平方差公式计算的是（）

A、(3a+b)(3b-a) B、 $(\frac{1}{3} a + 1) (- \frac{1}{3} a - 1)$ C、(a-b)(-a+b) D、(-a-b)(-a+b)

查看试题解析
8. 如图，一束光线从点C出发，经过平面镜 AB 反射后，沿与 AF 平行的线段 DE 射出（此时∠1=∠2），若测得 ∠DCF=100°，则 ∠A= （）

A、50° B、60° C、70° D、80°

查看试题解析
9. 如图B，E，C，F，四点在同一条直线上，EB=CF，∠DEF=∠ABC，添加以下哪一个条件不能判断 △ABC≌△DEF 的是（）

A、∠A=∠D B、DF∥AC C、AC=DF D、AB=DE

查看试题解析
10. 下列说法：①对顶角相等；②同位角相等；③必然事件发生的概率为；④等腰三角形的对称轴就是其底边上的高所在的直线，其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
11. 某天，小王去朋友家借书，在朋友家停留一段时间后，返回家中，如图是他离家的路程（千米）与时间（分）关系的图象，根据图象信息，下列说法正确的是（）

A、小王去时的速度大于回家的速度 B、小王去时走上坡路，回家时走下坡路 C、小王去时所花时间少于回家所花时间 D、小王在朋友家停留了分

查看试题解析
12. 如图，△ABC 中，AB=AC，AB 的垂直平分线交 AB 于点 D，交 CA 的延长线于点 E，∠EBC=42°，则 ∠BAC=（）

A、159° B、154° C、152° D、138°

查看试题解析

二、填空题

13. 一个不透明的布袋里装有 7个只有颜色不同的球，其中 4 个红球、 3个白球，从布袋中随机摸出一个球，则摸到红球的概率是．

查看试题解析
14. 如图，OC 平分 ∠AOB，D 为 OC 上一点，DE⊥OB 于 E，若 DE=5，则 D 到 OA 的距离为．

查看试题解析
15. 若 ${(x - y)}^{2} = 6$ ，xy=2，则 $x^{2} + y^{2} =$ ．

查看试题解析
16. 如图，把△ABC的中线CD延长到E，使DE=CD，连接AE，若AC=4且△BCD的周长比△ACD的周长大1，则AE= ．

查看试题解析

三、解答题

17. 计算：

(1)、 $2017^{0} + 8 \times 2^{- 1} - 2^{10} \div 2^{8}$ ；

(2)、 $（ 4 m^{3} n - m^{2} n^{2} + 2 m n^{2} - 2 m n) \div (2 m n)$ ．

查看试题解析
18. 先化简，再求值： $[（ x + y) (x - y) - {(x - y)}^{2} - y (x - 2 y)] \div (2 x)$ ，其中 $x = \frac{1}{2017}$ ， $y = - \frac{2}{3}$ ．

查看试题解析
19. 某商场为了吸引顾客，设立了一个可以自由转动的转盘（转盘被等分成个扇形，如图）并规定：顾客在本商场每消费元，就能获得一次转动转盘的机会，如果转盘停止后，指针正好对准红、黄或绿色区域，顾客就可以分别获得 100 元、 50 元、 20 元的购物券．某顾客消费 210 元，他转动转盘获得购物券的概率是多少?他得到 100 元、 50 元、 20 元购物券的概率分别是多少?

查看试题解析
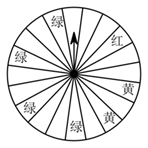20. 如图，点P与点 Q 都在y轴上，且关于x轴对称．

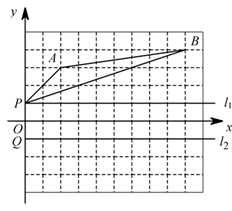(1)、请画出△ABP 关于x轴的对称图形 $△ A^{'} B^{'} Q$ （其中点 A 的对称点用 $A^{'}$ 表示，点的对称点用 $B^{'}$ 表示）；

(2)、点P ，Q 同时都从y轴上的位置出发，分别沿l₁ ， l₂方向，以相同的速度向右运动，在运动过程中是否在某个位置使得 $A P + B Q =$ $A^{'} B$ 成立?若存在，请你在图中画出此时 PQ 的位置（用线段 $P^{'} Q^{'}$ 表示），若不存在，请你说明理由（注：画图时，先用铅笔画好，再用钢笔描黑）．

查看试题解析
21. 如图，在 △ABC 中，∠C=90°，DB⊥BC 于点，分别以点 D 和点为圆心，以大于 $\frac{1}{2} D B$ 的长为半径作弧，两弧相交于点 E 和点，作直线 EF，延长 AB 于点，连接 DG，下面是说明 ∠A=∠D 的说理过程，请把下面的说理过程补充完整：
因为 DB⊥BC（已知），

所以 ∠DBC=90°(          ) ．

因为 ∠C=90°（已知），

所以 ∠DBC=∠C（等量代换），

所以 DB∥AC (          ) ，

所以                                （两直线平行，同位角相等）；

由作图法可知：直线 EF 是线段 DB 的 (          ) ，

所以 GD=GB，线段               （上的点到线段两端点的距离相等），

所以                                 (          ) ，因为 ∠A=∠1（已知），

所以 ∠A=∠D（等量代换）．

查看试题解析
22. 如图，AB∥CD，E 是直线 CD 上的一点，且 ∠BAE=30°， P是直线 CD 上的一动点，M是 AP 的中点，直线 MN⊥AP 且与 CD 交于点 N，设 ∠BAP=X°，∠MNE=Y°．

(1)、在图2 中，当 x=12 时，∠MNE=；在图 3 中，当 x=50 时，∠MNE=；

(2)、研究表明：y与x之间关系的图象如图4所示（不存在时，用空心点表示），请你根据图象直接估计当 y=100 时，x= ；

(3)、探究：当 x= 时，点 N 与点 E 重合；

(4)、探究：当 x>105 时，求y与x之间的关系式．

查看试题解析