广东省韶关市2017-2018学年七年级下学期数学期末考试试卷

试卷更新日期：2019-06-13 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各数中是无理数的是（）

A、3.14 B、 $\sqrt{4}$ C、 $\frac{2}{3}$ D、 $\sqrt{6}$

查看试题解析
2. 下列调查中，适合采用全面调查（普查）方式的是（）

A、对北江河水质情况的调查 B、对端午节期间市场上粽子质量情况的调查 C、对某班50名学生视力情况的调查 D、节能灯厂家对一批节能灯管使用寿命的调查

查看试题解析
3. 下列各点中，在第二象限的点是（）

A、（﹣3，2） B、（﹣3，﹣2） C、（3，2） D、（3，﹣2）

查看试题解析
4. 如图，下列条件中不能判定AB∥CD的是（）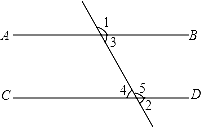

A、∠3=∠4 B、∠1=∠5 C、∠4+∠5=180° D、∠3+∠5=180°

查看试题解析
5. 不等式组 ${\begin{matrix} x > - 1 \\ x \leq 1 \end{matrix}$ 的解集在数轴上可表示为（）

A、 B、 C、 D、

查看试题解析
6. 若a＜b，则下列各式中，错误的是（）

A、a﹣3＜b﹣3 B、3﹣a＜3﹣b C、﹣3a＞﹣3b D、3a＜3b

查看试题解析
7. 下列命题：
①两条直线被第三条直线所截，同位角相等；

②两点之间，线段最短；

③相等的角是对顶角；

④同角或等角的补角相等。

其中是真命题的有（）个。

A、1 B、2 C、3 D、4

查看试题解析
8. 下列式子正确的是（）

A、 $\sqrt{9}$ =±3 B、 $\sqrt{- \frac{1}{9}} = - \frac{1}{3}$ C、 $\sqrt{{(- 2)}^{2}}$ =2 D、 $\sqrt[3]{- 9}$ =﹣3

查看试题解析
9. 若 ${\begin{matrix} x = 2 \\ y = 3 \end{matrix}$ 是关于x、y的二元一次方程2x+ay=10的一组解，则a的值为（）

A、2 B、﹣2 C、3 D、1

查看试题解析
10. 李明同学早上骑自行车上学，中途因道路施工步行一段路，到学校共用时15分钟．他骑自行车的平均速度是250米/分钟，步行的平均速度是80米/分钟．他家离学校的距离是2900米．如果他骑车和步行的时间分别为x、y分钟，列出的方程是（）

A、 ${\begin{array}{l} x + y = \frac{1}{4} \\ 250 x + 80 y = 2900 \end{array}$ B、 ${\begin{array}{l} x + y = 15 \\ 80 x + 250 y = 2900 \end{array}$ C、 ${\begin{array}{l} x + y = \frac{1}{4} \\ 80 x + 250 y = 2900 \end{array}$ D、 ${\begin{array}{l} x + y = 15 \\ 250 x + 80 y = 2900 \end{array}$

查看试题解析

二、填空题

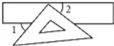
11. 将2x﹣y=1写成用含y的代数式表示x的形式，则x= ．

查看试题解析
12. 如图，把一块直角三角板的直角顶点放在直尺的一边上，若∠1=50°，则∠2=°．

查看试题解析
13. 某区为了了解14万名学生的数学成绩，从中抽取了1000名学生的数学成绩进行统计分析，这个问题中的样本容量是．

查看试题解析
14. 在平面直角坐标系中，若点A（m+1，m﹣7）在x轴上，则m= ．

查看试题解析
15. 若 $\sqrt{x - 3}$ +|1+y|=0，则x﹣y= ．

查看试题解析
16. 不等式2x+5＜11的正整数解是．

查看试题解析
17. 已知3x+2y=4，则6x+4y﹣7= ．

查看试题解析
18. 某试卷共有30道题，每道题选对得10分，选错了或者不选扣5分，至少要选对道题，其得分才能不少于80分．

查看试题解析
19. 如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点（1，1），第2次接着运动到点（2，0），第3次接着运动到点（3，2），……，按这样的运动规律，经过第100次运动后，动点P的坐标是．

查看试题解析

三、解答题

20. 计算：（﹣2）²+|1﹣ $\sqrt{2}$ |﹣ $\sqrt[3]{27}$

查看试题解析
21. 解不等式：4（x﹣1）+3≤3x

查看试题解析
22. 解方程组 ${\begin{matrix} x - y = 5 \\ 2 x + y = 4 \end{matrix}$ ．

查看试题解析
23. 解不等式组 ${\begin{matrix} x + 8 \leq 4 x - 1 \\ \frac{3 x - 4}{2} < x + 1 \end{matrix}$ ，并将其解集在数轴上表示出来．

查看试题解析
24. 如图，已知EF∥AD，∠1＝∠2.求证∠DGA＋∠BAC＝180°.请将下列证明过程填写完整：

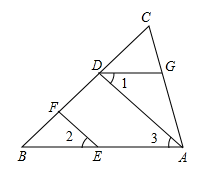
证明：∵EF∥AD(已知)，

∴∠2＝()．

又∵∠1＝∠2(已知)，

∴∠1＝∠3()．

∴AB∥()．

∴∠DGA＋∠BAC＝180°()．

查看试题解析
25. 在平面直角坐标系中，△ABC的位置如图所示，且顶点在网格格点上将△ABC向右平移7个单位长度，再向下平移2个单位长度得到△A₁B₁C₁ ．（图中每个小方格边长均为1个单位长度），请解决下列问题：

(1)、在图中画出平移后的△A₁B₁C₁；

(2)、直接写出点B₁、C₁的坐标：B₁（，），C₁（，）；

(3)、填空：△ABC的面积是（平方单位）．

查看试题解析
26. 某校为了了解七年级1000名学生的身体健康情况，从该年级随机抽取了若干名学生，将他们按体重（均为整数，单位：kg）分成五组（A：39.5﹣46.5；B：46.5﹣53.5；C：53.5﹣60.5；D：60.5﹣67.5；E：67.5﹣74.5），并依据统计数据绘制了如下两幅尚不完整的统计图．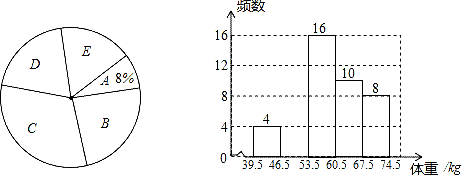

请解答下列问题：

(1)、这次随机抽取了名学生调查，并补全频数分布直方图；

(2)、在抽取调查的若干名学生中体重在组的人数最多，在扇形统计图中D组的圆心角是度；

(3)、请你估计该校七年级体重超过60kg的学生大约有多少名？

查看试题解析
27. 如图，AB∥CD，NC⊥MC，垂足为C，∠NCB=30°，CM平分∠BCE，求∠B的度数．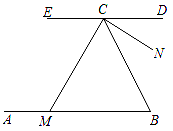

查看试题解析

28. 某学校准备购买A、B两种型号篮球，询问了甲、乙两间学校了解这两款篮球的价格，下表是甲、乙两所学校购买A、B两种型号篮球的情况：

购买学校	购买型号及数量（个）		购买支出款项（元）
购买学校	A	B	购买支出款项（元）
甲	3	8	622
乙	5	4	402

(1)、求A、B两种型号的篮球的销售单价；

(2)、若该学校准备用不多于1000元的金额购买这两种型号的篮球共20个，求A种型号的篮球最少能采购多少个？

查看试题解析

29. 在平面直角坐标系中，A（﹣2，0），C（2，2），过C作CB⊥x轴于B．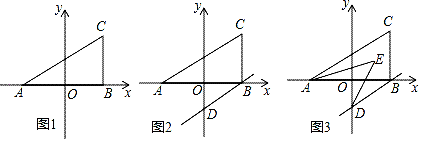

(1)、如图1，△ABC的面积是；

(2)、如图1，在y轴上找一点P，使得△ABP的面积与△ABC的面积相等，请直接写出P点坐标：；

(3)、如图2，若过B作BD∥AC交y轴于D，则∠BAC+∠ODB的度数为度；

(4)、如图3，BD∥AC，若AE、DE分别平分∠CAB，∠ODB，求∠AED的度数．

查看试题解析