广东省汕头市龙湖区2017-2018学年七年级下学期数学期末考试试卷
试卷更新日期:2019-06-13 类型:期末考试
一、单选题
-
1. 如图所示,∠1与∠2是对顶角的是( )A、
 B、
B、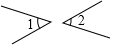 C、
C、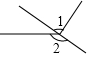 D、
D、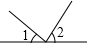 2. 下列调查中最适合采用全面调查的是( )A、调查某批次汽车的抗撞击能力 B、调查一批日光灯的使用寿命 C、调查某班40名同学的视力情况 D、调查全市中小学生的视力情况3. 下列方程是二元一次方程的是( )A、x﹣ =2 B、x+2y=0 C、x2﹣x=5 D、3x﹣1=04. 已知a>b,则下列不等式一定成立的是( )A、a+1<b+1 B、2a<2b C、a﹣b<0 D、﹣5a<﹣5b5. 不等式x﹣1<2的正整数解有( )A、1个 B、2个 C、3个 D、4个6. 下列各数中3.14, ,0.1010010001…,﹣ ,2π,﹣ 有理数的个数有( )A、1个 B、2个 C、3个 D、4个7. 在平面直角坐标系中,点(-7,-2m+1)在第三象限,则m的取值范围是( )A、m< B、m>- C、m<- D、m>8. 若方程6kx﹣2y=8有一组解 ,则k的值等于(( )A、 B、 C、 D、9. 如图,将三角形的直角顶点放在直尺的一边上,若∠1=65°,则∠2的度数为( )
2. 下列调查中最适合采用全面调查的是( )A、调查某批次汽车的抗撞击能力 B、调查一批日光灯的使用寿命 C、调查某班40名同学的视力情况 D、调查全市中小学生的视力情况3. 下列方程是二元一次方程的是( )A、x﹣ =2 B、x+2y=0 C、x2﹣x=5 D、3x﹣1=04. 已知a>b,则下列不等式一定成立的是( )A、a+1<b+1 B、2a<2b C、a﹣b<0 D、﹣5a<﹣5b5. 不等式x﹣1<2的正整数解有( )A、1个 B、2个 C、3个 D、4个6. 下列各数中3.14, ,0.1010010001…,﹣ ,2π,﹣ 有理数的个数有( )A、1个 B、2个 C、3个 D、4个7. 在平面直角坐标系中,点(-7,-2m+1)在第三象限,则m的取值范围是( )A、m< B、m>- C、m<- D、m>8. 若方程6kx﹣2y=8有一组解 ,则k的值等于(( )A、 B、 C、 D、9. 如图,将三角形的直角顶点放在直尺的一边上,若∠1=65°,则∠2的度数为( )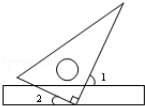 A、10° B、15° C、20° D、25°10. 有2元和5元两种纸币共21张,并且总钱数为72元,设2元纸币x张,5元纸币y张,根据题意列方程组为( )A、 B、 C、 D、
A、10° B、15° C、20° D、25°10. 有2元和5元两种纸币共21张,并且总钱数为72元,设2元纸币x张,5元纸币y张,根据题意列方程组为( )A、 B、 C、 D、二、填空题
-
11. ﹣8的立方根是 , 9的算术平方根是 .12. 点M(﹣3,4)到x轴的距离是;到y轴的距离是 .13. 用不等式表示:x与5的差不大于x的2倍: .14. 若 x5a+2b+1y2与5x6y3a﹣2b﹣1是同类项,则a= , b= .15. 如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2018次运动后,动点P的坐标是 .
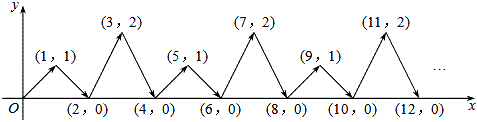
三、解答题
-
16. 计算:(﹣2)3× +(﹣1)2018+ .17. 解不等式组 并将其解集表示在数轴上.
 18. 解方程组:19. 已知一个正数的两个平方根分别是2a﹣1和a﹣5,求这个正数的值.20. 某学校对学生的课外阅读时间进行抽样调查,将收集的数据分成A、B、C、D、E五组进行整理,并绘制成如下的统计图表(图中信息不完整).
18. 解方程组:19. 已知一个正数的两个平方根分别是2a﹣1和a﹣5,求这个正数的值.20. 某学校对学生的课外阅读时间进行抽样调查,将收集的数据分成A、B、C、D、E五组进行整理,并绘制成如下的统计图表(图中信息不完整).组别
阅读时间x(时)
人数
A
0≤x<10
K
B
10≤x<20
100
C
20≤x<30
M
D
30≤x<40
140
E
x≥40
N
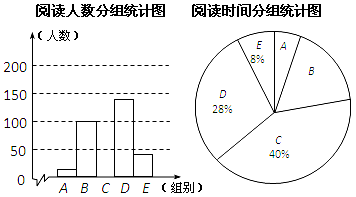
请结合以上信息解答下列问题
(1)、阅读时间分组统计表中k、m、n的值分别是、、;(2)、补全“阅读人数分组统计图”;(3)、若全校有3000名学生,请估算全校课外阅读时间在20小时以下(不含20小时)的21. 如图,一个四边形纸片 , ,把纸片按如图折叠,使点 落在 边上的 点, 是折痕. (1)、试判断 与 的位置关系;(2)、如果 ,求 的度数.22. 学校为数学竞赛准备了若干钢笔和笔记本(每支钢笔的价格相同,每本笔记本的价格相同)作为竞赛的奖品.若购买2支钢笔和3本笔记本需62元,购买5支钢笔和1本笔记本需90元.(1)、购买一支钢笔和一本笔记本各需多少钱?(2)、若学校准备购买钢笔和笔记本共80件奖品,并且购买的费用不超过1100元,则学校最多可以购买多少支钢笔?23. 已知,在直角坐标系中,有A(0,3),B(2,1),C(﹣3,﹣3)三点.
(1)、试判断 与 的位置关系;(2)、如果 ,求 的度数.22. 学校为数学竞赛准备了若干钢笔和笔记本(每支钢笔的价格相同,每本笔记本的价格相同)作为竞赛的奖品.若购买2支钢笔和3本笔记本需62元,购买5支钢笔和1本笔记本需90元.(1)、购买一支钢笔和一本笔记本各需多少钱?(2)、若学校准备购买钢笔和笔记本共80件奖品,并且购买的费用不超过1100元,则学校最多可以购买多少支钢笔?23. 已知,在直角坐标系中,有A(0,3),B(2,1),C(﹣3,﹣3)三点.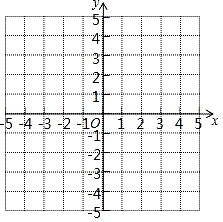 (1)、请在平面直角坐标系中描出各点,并画出三角形ABC;(2)、三角形ABC的面积是;(直接写出结果)(3)、设BC交y轴于点P,试求P点的坐标.24. 如图,长方形ABCD在平面直角坐标系中,已知点A(0,a),B(0,6),C(b,6),且满足a= +8.
(1)、请在平面直角坐标系中描出各点,并画出三角形ABC;(2)、三角形ABC的面积是;(直接写出结果)(3)、设BC交y轴于点P,试求P点的坐标.24. 如图,长方形ABCD在平面直角坐标系中,已知点A(0,a),B(0,6),C(b,6),且满足a= +8. (1)、请直接写出A、C、D三个点的坐标,A , C , D;(2)、连接线段BD、OD,试求三角形BOD的面积;(3)、若长方形ABCD以每秒1个单位长度匀速向下运动,设运动的时间为t秒,问是否存在某一时刻,三角形BOD的面积与长方形ABCD的面积相等?若存在,请求出t的值;若不存在,请说明理由.
(1)、请直接写出A、C、D三个点的坐标,A , C , D;(2)、连接线段BD、OD,试求三角形BOD的面积;(3)、若长方形ABCD以每秒1个单位长度匀速向下运动,设运动的时间为t秒,问是否存在某一时刻,三角形BOD的面积与长方形ABCD的面积相等?若存在,请求出t的值;若不存在,请说明理由.