广东省珠海市香洲区2017-2018学年八年级下学期数学期末考试试卷
试卷更新日期:2019-06-13 类型:期末考试
一、单选题
-
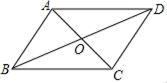
1. 下列二次根式中,属于最简二次根式的是( )A、 B、 C、 D、2. 直角三角形的两条直角边长分别为a和b , 斜边长为c , 已知c=13,b=5,则a=( )A、1 B、5 C、12 D、253. 矩形的对角线一定具有的性质是( )A、互相垂直 B、互相垂直且相等 C、相等 D、互相垂直平分4. 在今年的八年级期末考试中,我校(1)(2)(3)(4)班的平均分相同,方差分别为S12=20.8,S22=15.3,S32=17,S42=9.6,四个班期末成绩最稳定的是( )A、(1)班 B、(2)班 C、(3)班 D、(4)班5. 函数y=﹣2x+3的图象经过( )A、第一、二、三象限 B、第一、二、四象限 C、第二、三、四象限 D、第一、三、四象限6. 如图,下列哪组条件不能判定四边形ABCD是平行四边形( )
 A、AB∥CD , AB=CD B、AB∥CD , AD∥BC C、OA=OC , OB=OD D、AB∥CD , AD=BC7. 下列计算正确的是( )A、 B、 C、 D、8. 如图,直线y1=x+b与y2=kx-1相交于点P,点P的横坐标为-1,则关于x的不等式x+b>kx-1的解集在数轴上表示正确的是( )
A、AB∥CD , AB=CD B、AB∥CD , AD∥BC C、OA=OC , OB=OD D、AB∥CD , AD=BC7. 下列计算正确的是( )A、 B、 C、 D、8. 如图,直线y1=x+b与y2=kx-1相交于点P,点P的横坐标为-1,则关于x的不等式x+b>kx-1的解集在数轴上表示正确的是( ) A、
A、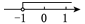 B、
B、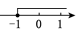 C、
C、 D、
D、 9. 如图,把一张正方形纸对折两次后,沿虚线剪下一角,展开后所得图形一定是( )
9. 如图,把一张正方形纸对折两次后,沿虚线剪下一角,展开后所得图形一定是( ) A、三角形 B、菱形 C、矩形 D、正方形10. 如图,正方形ABCD的边长为4cm,动点P从点A出发,沿A→D→C的路径以每秒1cm的速度运动(点P不与点A、点C重合),设点P运动时间为x秒,四边形ABCP的面积为ycm2 , 则下列图象能大致反映y与x的函数关系的是( )
A、三角形 B、菱形 C、矩形 D、正方形10. 如图,正方形ABCD的边长为4cm,动点P从点A出发,沿A→D→C的路径以每秒1cm的速度运动(点P不与点A、点C重合),设点P运动时间为x秒,四边形ABCP的面积为ycm2 , 则下列图象能大致反映y与x的函数关系的是( )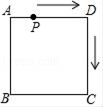 A、
A、 B、
B、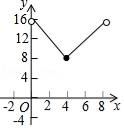 C、
C、 D、
D、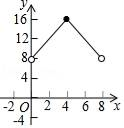
二、填空题
-
11. 已知一组数据3、x、4、5、6的众数是6,则x的值是 .12. 若 有意义,则字母x的取值范围是 .13. 定理“对角线互相平分的四边形是平行四边形”的逆定理是 .14. 将直线y=2x向上平移3个单位所得的直线解析式是 .15. 在正方形ABCD中,对角线AC=2cm,那么正方形ABCD的面积为 .16. 如图,已知等边三角形ABC边长为1,△ABC的三条中位线组成△A1B1C1 , △A1B1C1的三条中位线组成△A2B2C2 , 依此进行下去得到△A5B5C5的周长为 .

三、解答题
-
17. 计算:18. 已知矩形周长为18,其中一条边长为x,设另一边长为y.(1)、写出y与x的函数关系式;(2)、求自变量x的取值范围.19. 如图,E、F分别平行四边形ABCD对角线BD上的点,且BE=DF.
求证:∠DAF=∠BCE.
 20. 某工厂甲、乙两个部门各有员工400人,为了解这两个部门员工的生产技能情况,进行了抽样调查,过程如下,请补充完整.
20. 某工厂甲、乙两个部门各有员工400人,为了解这两个部门员工的生产技能情况,进行了抽样调查,过程如下,请补充完整.收集数据从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分制)如下:
甲 78 86 74 81 75 76 87 70 75 90
75 79 81 70 74 80 86 69 83 77
乙 93 73 88 81 72 81 94 83 77 83
80 81 70 81 73 78 82 80 70 40
整理、描述数据
按如下分数段整理、描述这两组样本数据:
成绩
人数
部门
40≤x≤49
50≤x≤59
60≤x≤69
70≤x≤79
80≤x≤89
90≤x≤100
甲
0
0
1
11
7
1
乙
(说明:成绩80分及以上为生产技能优秀,70~79分为生产技能良好,60~69分为生产技能合格,60分以下为生产技能不合格)
分析数据
两组样本数据的平均数、中位数、众数如下表所示:
部门
平均数
中位数
众数
甲
78.3
77.5
75
乙
78
80.5
81
得出结论:
.估计乙部门生产技能优秀的员工人数为;
.可以推断出部门员工的生产技能水平较高,理由为.(至少从两个不同的角度说明推断的合理性)
21. 如图,在△ABC中,E点是AC的中点,其中BD=2,DC=6,BC=2 ,AD= ,求DE的长. 22. 珠海长隆海洋王国暑假期间推出了两套优惠方案:①购买成人票两张以上(包括两张),则儿童票按6折出售;②成人票和儿童票一律按8.5折出售,已知成人票是350元/张,儿童票是240元/张,张华准备暑假期间带家人到长隆海洋王国游玩,准备购买8张成人票和若干张儿童票.(1)、请分别写出两种优惠方案中,购买的总费用y(元)与儿童人数x(人)之间的函数关系式;(2)、对x的取值情况进行分析,说明选择哪种方案购票更省钱.23. 在矩形ABCD中,AB=8,BC=6,点E是AB边上一点,连接CE,把△BCE沿CE折叠,使点B落在点B′处.
22. 珠海长隆海洋王国暑假期间推出了两套优惠方案:①购买成人票两张以上(包括两张),则儿童票按6折出售;②成人票和儿童票一律按8.5折出售,已知成人票是350元/张,儿童票是240元/张,张华准备暑假期间带家人到长隆海洋王国游玩,准备购买8张成人票和若干张儿童票.(1)、请分别写出两种优惠方案中,购买的总费用y(元)与儿童人数x(人)之间的函数关系式;(2)、对x的取值情况进行分析,说明选择哪种方案购票更省钱.23. 在矩形ABCD中,AB=8,BC=6,点E是AB边上一点,连接CE,把△BCE沿CE折叠,使点B落在点B′处. (1)、当B′在边CD上时,如图①所示,求证:四边形BCB′E是正方形;(2)、当B′在对角线AC上时,如图②所示,求BE的长.24. 如图,一次函数y=kx+b的图象经过点A(0,4)和点B(3,0),以线段AB为边在第一象限内作等腰直角△ABC,使∠BAC=90°.
(1)、当B′在边CD上时,如图①所示,求证:四边形BCB′E是正方形;(2)、当B′在对角线AC上时,如图②所示,求BE的长.24. 如图,一次函数y=kx+b的图象经过点A(0,4)和点B(3,0),以线段AB为边在第一象限内作等腰直角△ABC,使∠BAC=90°. (1)、求一次函数的解析式;(2)、求出点C的坐标;(3)、点P是y轴上一动点,当PB+PC最小时,求点P的坐标.25. 如图,菱形ABCD中,AB=6cm,∠ADC=60°,点E从点D出发,以1cm/s的速度沿射线DA运动,同时点F从点A出发,以1cm/s的速度沿射线AB运动,连接CE、CF和EF,设运动时间为t(s).
(1)、求一次函数的解析式;(2)、求出点C的坐标;(3)、点P是y轴上一动点,当PB+PC最小时,求点P的坐标.25. 如图,菱形ABCD中,AB=6cm,∠ADC=60°,点E从点D出发,以1cm/s的速度沿射线DA运动,同时点F从点A出发,以1cm/s的速度沿射线AB运动,连接CE、CF和EF,设运动时间为t(s).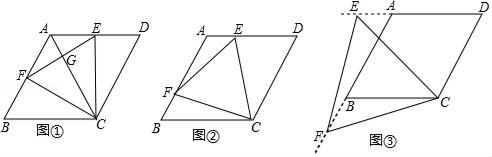 (1)、当t=3s时,连接AC与EF交于点G,如图①所示,则AG=cm;(2)、当E、F分别在线段AD和AB上时,如图②所示,求证△CEF是等边三角形;(3)、当E、F分别运动到DA和AB的延长线上时,如图③所示,若CE= cm,求t的值和点F到BC的距离.
(1)、当t=3s时,连接AC与EF交于点G,如图①所示,则AG=cm;(2)、当E、F分别在线段AD和AB上时,如图②所示,求证△CEF是等边三角形;(3)、当E、F分别运动到DA和AB的延长线上时,如图③所示,若CE= cm,求t的值和点F到BC的距离.