广东省深圳市宝安区2017-2018学年八年级下学期数学期末考试试卷

试卷更新日期：2019-06-13 类型：期末考试

进入出卷网下载

一、单选题

1. 如果分式 $\frac{1}{x + 3}$ 有意义，则x的取值范围是（）

A、x＝﹣3 B、x＞﹣3 C、x≠﹣3 D、x＜﹣3

查看试题解析
2. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 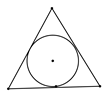B、 C、 D、

查看试题解析
3. 已知实数a，b，若a＞b，则下列结论错误的是（）

A、a+6＞b+6 B、a﹣2＞b﹣2 C、﹣2a＞﹣2b D、 $\frac{a}{3} > \frac{b}{3}$

查看试题解析
4. 将点A（1，﹣1）向上平移2个单位后，再向左平移3个单位，得到点B，则点B的坐标为（）

A、（﹣2，1） B、（﹣2，﹣1） C、（2，1） D、（2，﹣1）

查看试题解析
5. 若一个多边形的内角和为1080°，则这个多边形的边数为（）
　

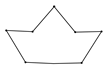A、6 B、7 C、8 D、9

查看试题解析
6. 下列多项式中，可以提取公因式的是（）

A、ab+cd B、mn+m² C、x²-y² D、x²+2xy+y²

查看试题解析
7. 如图，在平行四边形ABCD中，DE平分∠ADC ， AD=8，BE=3，则平行四边形ABCD的周长是（）

A、16 B、14 C、26 D、24

查看试题解析
8. 下列命题中，错误的是（）

A、过n边形一个顶点的所有对角线，将这个多边形分成（n﹣2）个三角形 B、三角形中，到三个顶点距离相等的点是三条边垂直平分线的交点 C、三角形的中线将三角形分成面积相等的两部分 D、一组对边平行另一组对边相等的四边形是平行四边形

查看试题解析
9. 如图，在△ABC中，∠ACB=90°，分别以点A和点B为圆心以相同的长（大于 $\frac{1}{2}$ AB）为半径作弧，两弧相交于点M和N点，作直线MN交AB于点D，交BC于点E，若AC=3，BC=4，则BE等于（）

A、 $\frac{3}{2}$ B、 $\frac{9}{4}$ C、 $\frac{15}{4}$ D、 $\frac{25}{8}$

查看试题解析
10. 某次知识竞赛共有30道题，每一题答对得5分，答错或不答都扣3分，小亮得分要超过70分，他至少要答对多少道题？如果设小亮答对了x道题，根据题意列式得（）

A、5x﹣3（30﹣x）＞70 B、5x+3（30﹣x）≤70 C、5x﹣3（30+x）≥70 D、5x+3（30﹣x）＞70

查看试题解析
11. 如图，直线y=kx+b与y=mx+n分别交x轴于点A（﹣0.5，0）、B（2，0），则不等式（kx+b）（mx+n）＜0的解集为（）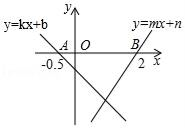

A、x＞2 B、﹣0.5＜x＜2 C、0＜x＜2 D、x＜﹣0.5或x＞2

查看试题解析
12. 如图，平行四边形 ABCD 中，AD∥BC，AB=BC=CD=AD=4，∠A=∠C=60°，连接 BD，将△BCD 绕点 B 旋转，当 BD（即 BD′）与 AD 交于一点 E，BC（即 BC′）同时与 CD 交于一点 F 时，下列结论正确的是（）
①AE=DF；②∠BEF=60°；③∠DEB=∠DFB；④△DEF 的周长的最小值是4+2 $\sqrt{3}$

A、①② B、②③ C、①②④ D、①②③④

查看试题解析

二、填空题

13. 因式分解：3a²﹣27= ．

查看试题解析
14. 已知 $\frac{x y}{x + y} = \frac{3}{5}$ ，则 $\frac{1}{x} + \frac{1}{y}$ = ．

查看试题解析
15. 请观察一列分式：﹣ $\frac{x}{y^{3}} ， \frac{x^{2}}{y^{5}}$ ，﹣ $\frac{x^{3}}{y^{7}} ， \frac{x^{4}}{y^{9}}$ ，…则第11个分式为．

查看试题解析
16. 如图，等腰Rt△ABC中，∠BAC=90°，AB=AC=10，等腰直角三角形ADE绕着点A旋转，∠DAE=90°，AD=AE=6，连接BD、CD、CE，点M、P、N分别为DE、DC、BC的中点，连接MP、PN、MN，则△PMN的面积最大值为．

查看试题解析

三、解答题

17. 解不等式组 ${\begin{matrix} x + 4 > 1 - x \\ \frac{1}{2} x \leq \frac{1}{3} (x + 1) \end{matrix}$ ，并写出它的整数解．

查看试题解析
18. 先化简，再求值： $(\frac{1}{m + 2} + \frac{1}{m - 2}) \div \frac{2 m}{m^{2} - 4 m + 4}$ ，其中m=4．

查看试题解析
19. 解方程： $\frac{3 x}{3 - x}$ =2﹣ $\frac{3}{x - 3}$

查看试题解析
20. 在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系， $Δ A B C$ 的顶点都在格点上，请解答下列问题：

(1)、作出 $Δ A B C$ 向左平移4个单位长度后得到的 $Δ A_{1} B_{1} C_{1}$ ，并写出点 $C_{1}$ 的坐标；

(2)、将 $Δ A_{1} B_{1} C_{1}$ 绕原点 $O$ 逆时针旋转 $90 °$ 得到 $Δ A_{2} B_{2} C_{2}$ ，请画出旋转后的 $Δ A_{2} B_{2} C_{2}$ ，并写出点 $C_{2}$ 的坐标．

查看试题解析
21. 如图，AC是平行四边形ABCD的对角线，E、H分别为边BA和边BC延长线上的点，连接EH交AD、CD于点F、G，且EH∥AC．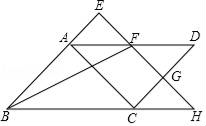

(1)、求证：EG=FH；

(2)、若△ACD是等腰直角三角形，∠ACD=90°，F是AD的中点，AD=6，连接BF，求BF的长．

查看试题解析
22. 为迎接全国文明城市的评选，市政府决定对春风路进行市政化改造，经过市场招标，决定聘请甲、乙两个工程队合作施工，已知春风路全长24千米，甲工程队每天施工的长度比乙工程队每天施工长度的多施工0.4千米，由甲工程队单独施工完成任务所需要的天数是乙工程队单独完成任务所需天数的 $\frac{5}{6}$ ．

(1)、求甲、乙两个工程队每天各施工多少千米？

(2)、若甲工程队每天的施工费用为0.8万元，乙工程队每天的施工费用为0.5万元，要使两个工程队施工的总费用不超过7万元，则甲工程队至多施工多少天？

查看试题解析
23. 如图1，已知平行四边形ABCO，以点O为原点，OC所在的直线为x轴，建立直角坐标系，AB交y轴于点D，AD=2，OC=6，∠A=60°，线段EF所在的直线为OD的垂直平分线，点P为线段EF上的动点，PM⊥x轴于点M点，点E与E′关于x轴对称，连接BP、E′M．

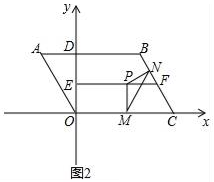(1)、请直接写出点A的坐标为，点B的坐标为；

(2)、当BP+PM+ME′的长度最小时，请直接写出此时点P的坐标为；

(3)、如图2，点N为线段BC上的动点且CM=CN，连接MN，是否存在点P，使△PMN为等腰三角形？若存在，请求出所有满足要求的EP的值；若不存在，请说明理由．

查看试题解析