广东省汕头市澄海区2017-2018学年八年级下学期数学期末考试试卷

试卷更新日期：2019-06-13 类型：期末考试

进入出卷网下载

一、单选题

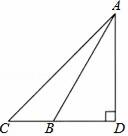
1. 计算 $\sqrt{{(- 4)}^{2}}$ 的结果是（）

A、16 B、4 C、2 D、-4

查看试题解析
2. 若 $\sqrt{75}$ 与最简二次根式 $\sqrt{m + 1}$ 是同类二次根式，则m的值为（）

A、7 B、11 C、2 D、1

查看试题解析
3. 若一个三角形三个内角度数的比为1：2：3，且最大的边长为2 $\sqrt{3}$ ，那么最小的边长为（）

A、1 B、 $\sqrt{3}$ C、2 D、4 $\sqrt{3}$

查看试题解析
4. 如图，在△ABC中，若AB＝AC＝6，BC＝4，D是BC的中点，则AD的长等于（）

A、4 $\sqrt{2}$ B、2 $\sqrt{5}$ C、2 $\sqrt{10}$ D、4

查看试题解析
5. 下列计算正确的是（）

A、 $\sqrt{3} + \sqrt{2} = \sqrt{5}$ B、5 $\sqrt{3} \cdot 5 \sqrt{2}$ =5 $\sqrt{6}$ C、 $\sqrt{12}$ $\div \sqrt{3} = 4$ D、 $\sqrt{8} - \sqrt{2} = \sqrt{2}$

查看试题解析
6. 在一次函数y＝kx+1中，若y随x的增大而增大，则它的图象不经过第（）象限

A、四 B、三 C、二 D、一

查看试题解析
7. 如图，▱ABCD的对角线AC、BD相交于点O ，已知AD＝10，BD＝14，AC＝8，则△OBC的周长为（）

A、16 B、19 C、21 D、28

查看试题解析
8. 已知一次函数y＝（m+1）x+m²﹣1的图象经过原点，则m的值为（（）

A、0 B、﹣1 C、1 D、±1

查看试题解析
9. 如图，已知直线l₁∥l₂∥l₃∥l₄ ，相邻两条平行线间的距离都是1，正方形ABCD的四个顶点分别在四条直线上，则正方形ABCD的面积为（）

A、 $\sqrt{3}$ B、 $\sqrt{5}$ C、3 D、5

查看试题解析
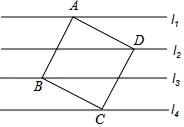10. 如图，在矩形纸片ABCD中，AD＝4cm ，把纸片沿直线AC折叠，使点D落在E处，CE交AB于点O ，若BO＝3m ，则AC的长为（）

A、6cm B、8cm C、5 $\sqrt{2}$ cm D、4 $\sqrt{5}$ cm

查看试题解析

二、填空题

11. |1﹣ $\sqrt{3}$ |＝．

查看试题解析
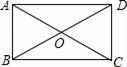
12. 使 $\sqrt{6 - x}$ 为整数的x的值可以是（只需填一个）．

查看试题解析
13. 一组数据2，3，x ， 5，7的平均数是4，则这组数据的众数是

查看试题解析
14. 如图，在矩形ABCD中，对角线AC、BD交于点O ， ∠AOD＝120°，对角线AC＝4，则BC的长为．

查看试题解析
15. 如图，小明同学在东西方向的环海路A处，测得海中灯塔P在北偏东60°方向上，在A处向正东方向行了100米到达B处，测得海中灯塔P在北偏东30°方向上，则灯塔P到环海路的距离PC＝米．

查看试题解析
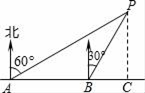16. 如图，在平面直角坐标系中，直线l：y=x+2交x轴于点A，交y轴于点A₁ ，点A₂ ， A₃ ， …在直线l上，点B₁ ， B₂ ， B₃ ， …在x轴的正半轴上，若△A₁OB₁ ， △A₂B₁B₂ ， △A₃B₂B₃ ， …，依次均为等腰直角三角形，直角顶点都在x轴上，则第n个等腰直角三角形A_nB_n_﹣₁B_n顶点B_n的横坐标为．

查看试题解析

三、解答题

17. 计算： $\sqrt{32}$ + $\frac{\sqrt{3} \times \sqrt{18}}{\sqrt{6}}$ － $\frac{3}{\sqrt{2}}$ － $\sqrt{\frac{1}{2}}$

查看试题解析
18. 已知一次函数y＝kx+b的图象与直线y＝﹣2x+1的交点M的横坐标为1，与直线y＝x﹣1的交点N的纵坐标为2，求这个一次函数的解析式．

查看试题解析
19. 如图，长4m的楼梯AB的倾斜角∠ABD为60°，为了改善楼梯的安全性能，准备重新建造楼梯，使其倾斜角∠ACD为45°，求调整后的楼梯AC的长．

查看试题解析
20. 为了推动阳光体育运动的广泛开展，引导学生走向操场，走进大自然，走到阳光下，积极参加体育锻炼，学校准备购买一批运动鞋供学生借用，现从各年级随机抽取了部分学生的鞋号，绘制了如下的统计图①和图②，请根据相关信息，解答下列问题：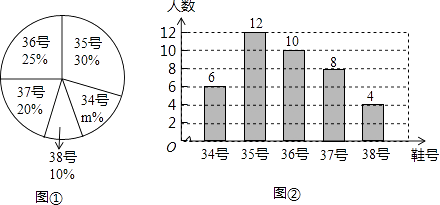

(1)、本次接受随机抽样调查的学生人数为，图①中m的值为；

(2)、求本次调查获取的样本数据的众数和中位数；

(3)、根据样本数据，若学校计划购买200双运动鞋，建议购买35号运动鞋多少双？

查看试题解析
21. 若x、y都是实数，且y＝ $\sqrt{x - 2}$ + $\sqrt{2 - x}$ + $\sqrt{2}$ ，求x²y+xy²的值．

查看试题解析
22. 如图，已知DB∥AC ， E是AC的中点，DB＝AE ，连结AD、BE ．

(1)、求证：四边形DBCE是平行四边形；

(2)、若要使四边形ADBE是矩形，则△ABC应满足什么条件？说明你的理由．

查看试题解析
23. 某商场计划购进A，B两种新型节能台灯共100盏，这两种台灯的进价、售价如表所示：

类型价格

进价(元/盏)

售价(元/盏)

A型

30

45

B型

50

70

(1)、若商场预计进货款为3500元，则这两种台灯各购进多少盏？

(2)、若商场规定B型台灯的进货数量不超过A型台灯数量的4倍，应怎样进货才能使商场在销售完这批台灯时获利最多？此时利润为多少元？

查看试题解析
24. 如图，在正方形ABCD中，AB＝6，点E在边CD上，且CE＝2DE ，将△ADE沿AE对折得到△AFE ，延长EF交边BC于点G ，连结AG、CF ．

(1)、求证：△ABG≌△AFG；

(2)、判断BG与CG的数量关系，并证明你的结论；

(3)、作FH⊥CG于点H ，求GH的长．

查看试题解析
25. 如图所示，已知直线L过点A（0，1）和B（1，0），P是x轴正半轴上的动点，OP的垂直平分线交L于点Q ，交x轴于点M ．

(1)、直接写出直线L的解析式；

(2)、设OP＝t ， △OPQ的面积为S ，求S关于t的函数关系式；并求出当0＜t＜2时，S的最大值；

(3)、直线L₁过点A且与x轴平行，问在L₁上是否存在点C ，使得△CPQ是以Q为直角顶点的等腰直角三角形？若存在，求出点C的坐标，并证明；若不存在，请说明理由．

查看试题解析

类型价格	进价(元/盏)	售价(元/盏)
A型	30	45
B型	50	70