广东省江门市江海区2017-2018学年八年级下学期数学期末考试试卷
试卷更新日期:2019-06-13 类型:期末考试
一、单选题
-
1. =( )A、4 B、2 C、﹣2 D、±22. 一组数据5,8,8,12,12,12,44的众数是( )A、5 B、8 C、12 D、443. 若点(3,1)在一次函数y=kx-2(k≠0)的图象上,则k的值是( )A、5 B、4 C、3 D、14. 如图,矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴的正半轴于M,则点M的表示的数为( )
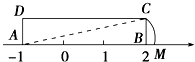 A、(2,0) B、( ,0) C、( ,0) D、( ,0)5. Rt△ABC中,斜边BC=2,则AB2+BC2+CA2=( )A、8 B、6 C、4 D、无法计算6. 在平面直角坐标系中,函数y=(k﹣1)x+(k+2)(k﹣2)的图象不经过第二象限与第四象限,则常数k满足( )A、k=2 B、k=﹣2 C、k=1 D、k>17. 关于四边形ABCD:①两组对边分别平行;②两组对边分别相等;③有一组对边平行且相等;④对角线AC和BD相等;以上四个条件中可以判定四边形ABCD是平行四边形的有( )A、1个 B、2个 C、3个 D、4个8. 如图,矩形ABCD中,DE⊥AC于E,且∠ADE:∠EDC=3:2,则∠BDE的度数为( )
A、(2,0) B、( ,0) C、( ,0) D、( ,0)5. Rt△ABC中,斜边BC=2,则AB2+BC2+CA2=( )A、8 B、6 C、4 D、无法计算6. 在平面直角坐标系中,函数y=(k﹣1)x+(k+2)(k﹣2)的图象不经过第二象限与第四象限,则常数k满足( )A、k=2 B、k=﹣2 C、k=1 D、k>17. 关于四边形ABCD:①两组对边分别平行;②两组对边分别相等;③有一组对边平行且相等;④对角线AC和BD相等;以上四个条件中可以判定四边形ABCD是平行四边形的有( )A、1个 B、2个 C、3个 D、4个8. 如图,矩形ABCD中,DE⊥AC于E,且∠ADE:∠EDC=3:2,则∠BDE的度数为( ) A、36° B、9° C、27° D、18°9. 如图,正方形ABCD的边长为4,P为正方形边上一动点,沿A→D→C→B→A 的路径匀速移动,设P点经过的路径长为x,△APD的面积是y,则下列图象能大致反映y与x的函数关系的是( )
A、36° B、9° C、27° D、18°9. 如图,正方形ABCD的边长为4,P为正方形边上一动点,沿A→D→C→B→A 的路径匀速移动,设P点经过的路径长为x,△APD的面积是y,则下列图象能大致反映y与x的函数关系的是( ) A、
A、 B、
B、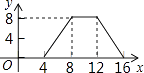 C、
C、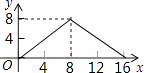 D、
D、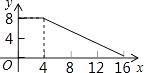 10. 如图,E是边长为4的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BR于点R,则PQ+PR的值是( )
10. 如图,E是边长为4的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BR于点R,则PQ+PR的值是( )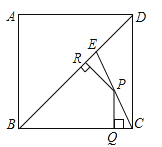 A、2 B、2 C、2 D、
A、2 B、2 C、2 D、二、填空题
-
11. 将一次函数y=3x﹣1的图象沿y轴向平移个单位后,得到的图象经过原点.12. 实验中学规定学生学期的数学成绩满分为120分,其中平时成绩占20%,期中考试成绩占30%,期末考试成绩占50%,王玲的三项成绩依次是100分,90分,106分,那么王玲这学期的数学成绩为 分.13. 如图,菱形ABCD的对角线AC与BD相交于点O,OE∥DC交BC于点E,AD=10cm,则OE的长为 .
 14. 已知一次函数y=ax+b的图象经过点(﹣2,0)和点(0,﹣1),则不等式ax+b>0的解集是 .15. 在直角坐标系中,直线y=x+1与y轴交于点A,按如图方式作正方形A1B1C1O、A2B2C2C1、A3B3C3C2…,A1、A2、A3…在直线y=x+1上,点C1、C2、C3…在x轴上,图中阴影部分三角形的面积从左到右依次记为S1、S2、S3、…Sn , 则Sn的值为(用含n的代数式表示,n为正整数).
14. 已知一次函数y=ax+b的图象经过点(﹣2,0)和点(0,﹣1),则不等式ax+b>0的解集是 .15. 在直角坐标系中,直线y=x+1与y轴交于点A,按如图方式作正方形A1B1C1O、A2B2C2C1、A3B3C3C2…,A1、A2、A3…在直线y=x+1上,点C1、C2、C3…在x轴上,图中阴影部分三角形的面积从左到右依次记为S1、S2、S3、…Sn , 则Sn的值为(用含n的代数式表示,n为正整数).
三、解答题
-
16. 计算:17. 已知,如图,平行四边形ABCD中,E是BC边的中点,连DE并延长交AB的延长线于点F.
求证:AB=BF.
 18. 已知一次函数y=kx+b的图象经过点(0,1)和(1,﹣2).(1)、求函数的解析式;(2)、求直线y=kx+b上到x轴距离为7的点的坐标.19. 如图,BD是矩形ABCD的一条对角线.
18. 已知一次函数y=kx+b的图象经过点(0,1)和(1,﹣2).(1)、求函数的解析式;(2)、求直线y=kx+b上到x轴距离为7的点的坐标.19. 如图,BD是矩形ABCD的一条对角线.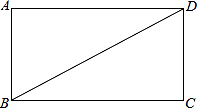 (1)、作BD的垂直平分线EF,分别交AD、BC于点E、F,垂足为点O(用尺规作图,保留作图痕迹,不要求写作法);(2)、求证:AF=CE.20. 2017年5月,举世瞩目的“一带一路”国际合作高峰论坛在北京举行.为了让学生更深刻地了解这一普惠世界的中国创举,某校组织八年级甲班和乙班的学生开展“一带一路”知识竞赛活动.现场决赛时,甲班和乙班分别选5名同学参加比赛,成绩如图所示:
(1)、作BD的垂直平分线EF,分别交AD、BC于点E、F,垂足为点O(用尺规作图,保留作图痕迹,不要求写作法);(2)、求证:AF=CE.20. 2017年5月,举世瞩目的“一带一路”国际合作高峰论坛在北京举行.为了让学生更深刻地了解这一普惠世界的中国创举,某校组织八年级甲班和乙班的学生开展“一带一路”知识竞赛活动.现场决赛时,甲班和乙班分别选5名同学参加比赛,成绩如图所示: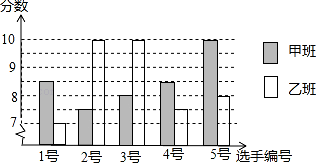 (1)、根据上图将计算结果填入下表:
(1)、根据上图将计算结果填入下表:平均数
中位数
众数
方差
甲班
8.5
8.5
乙班
8.5
10
1.6
(2)、你认为哪个班的成绩较好?为什么?21. 如图,函数y=﹣ x+2的图象与x轴、y轴分别交于点A、B,与函数y=kx(k为常数)的图象交于点E,以BE、OE为邻边的平行四边形是菱形. (1)、求k;(2)、过点B作y轴的垂线,交函数y=kx的图象于点C,四边形OACB是矩形吗?为什么?22. 如图,AD是△ABC的边BC的中线,E是AD的中点,过点A作AF∥BC,交BE的延长线于点F,连接CF,BF交AC于G.
(1)、求k;(2)、过点B作y轴的垂线,交函数y=kx的图象于点C,四边形OACB是矩形吗?为什么?22. 如图,AD是△ABC的边BC的中线,E是AD的中点,过点A作AF∥BC,交BE的延长线于点F,连接CF,BF交AC于G.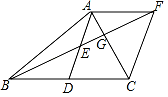 (1)、若四边形ADCF是菱形,试证明△ABC是直角三角形;(2)、求证:CG=2AG.23. 某市为节约水资源,制定了新的居民用水收费标准.按照新标准,用户每月缴纳的水费y(元)与每月用水量x(m3)之间的关系如图所示.
(1)、若四边形ADCF是菱形,试证明△ABC是直角三角形;(2)、求证:CG=2AG.23. 某市为节约水资源,制定了新的居民用水收费标准.按照新标准,用户每月缴纳的水费y(元)与每月用水量x(m3)之间的关系如图所示.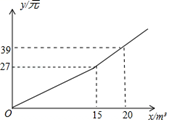 (1)、求y关于x的函数解析式;(2)、若某用户二、三月份共用水40m3(二月份用水量不超过25m3),缴纳水费79.8元,则该用户二、三月份的用水量各是多少m3?24. 如图,在正方形ABCD中,AB=4,P是CD边上的动点(P点不与C、D重合),过点P作直线与BC的延长线交于点E,与AD交于点F,且CP=CE,连接DE、BP、BF,设CP=x,△PBF的面积为S1 , △PDE的面积为S2
(1)、求y关于x的函数解析式;(2)、若某用户二、三月份共用水40m3(二月份用水量不超过25m3),缴纳水费79.8元,则该用户二、三月份的用水量各是多少m3?24. 如图,在正方形ABCD中,AB=4,P是CD边上的动点(P点不与C、D重合),过点P作直线与BC的延长线交于点E,与AD交于点F,且CP=CE,连接DE、BP、BF,设CP=x,△PBF的面积为S1 , △PDE的面积为S2 (1)、求证:BP⊥DE;(2)、求S1﹣S2关于x的函数解析式,并写出x的取值范围;(3)、当∠PBF=30°时,求S1﹣S2的值.
(1)、求证:BP⊥DE;(2)、求S1﹣S2关于x的函数解析式,并写出x的取值范围;(3)、当∠PBF=30°时,求S1﹣S2的值.