2016-2017学年浙江省杭州市萧山区戴村片八年级下学期期中数学试卷

试卷更新日期：2017-05-27 类型：期中考试

进入出卷网下载

一、仔细选一选

1. 要使式子 $\sqrt{2 - x}$ 有意义，则x的取值范围是（）

A、x＞0 B、x≥﹣2 C、x≥2 D、x≤2

查看试题解析
2. 下列运算正确的是（）

A、 $2 \sqrt{3} - \sqrt{3} = 1$ B、 ${(- \sqrt{2})}^{2} = 2$ C、 $\sqrt{{(- 11)}^{2}} = \pm 11$ D、 $\sqrt{3^{2} - 2^{2}} = \sqrt{3^{2}} - \sqrt{2^{2}} = 3 - 2 = 1$

查看试题解析
3. 下列方程是一元二次方程的是（　　）

A、x²﹣y=1 B、x²+2x﹣3=0 C、x²+ $\frac{1}{x}$ =3 D、x﹣5y=6

查看试题解析
4. 在某校“我的中国梦”演讲比赛中，有9名学生参加比赛，他们决赛的最终成绩各不相同，其中的一名学生要想知道自己能否进入前5名，不仅要了解自己的成绩，还要了解这9名学生成绩的（　　）

A、众数 B、方差 C、平均数 D、中位数

查看试题解析
5. 用配方法解一元二次方程x²﹣8x+7=0，方程可变形为（）

A、（x+4）²=9 B、（x﹣4）²=9 C、（x﹣8）²=16 D、（x+8）²=57

查看试题解析
6. 如图，平行四边形ABCD中，E，F是对角线BD上的两点，如果添加一个条件使△ABE≌△CDF，则添加的条件 $\underset{˙}{不} \underset{˙}{能}$ 是（）

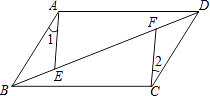A、AE=CF B、BE=FD C、BF=DE D、∠1=∠2

查看试题解析
7. 如果关于x的一元二次方程x²+px+q=0的两根分别为x₁=3，x₂=1，那么这个一元二次方程是（）

A、x²+3x+4=0 B、x²+4x﹣3=0 C、x²﹣4x+3=0 D、x²+3x﹣4=0

查看试题解析
8. 某课外小组的同学们在社会实践活动中调查了20户家庭某月的用电量，如表所示：
用电量（度）
120
140
160
180
200
户数
2
3
6
7
2
则这20户家庭该月用电量的众数和中位数分别是（）

A、180，160 B、160，180 C、160，160 D、180，180

查看试题解析
9. 根据下列表格中关于x的代数式ax²+bx+c的值与x的对应值，判断方程ax²+bx+c=0（a≠0，a，b，c为常数）的一个解的范围是（）
x
5.12
5.13
5.14
5.15
ax²+bx+c
﹣0.04
﹣0.02
0.01
0.03

A、5.14＜x＜5.15 B、5.13＜x＜5.14 C、5.12＜x＜5.13 D、5.10＜x＜5.12

查看试题解析
10. 关于x的方程x²+2kx+k﹣1=0的根的情况描述正确的是（）

A、k为任何实数，方程都没有实数根 B、k为任何实数，方程都有两个不相等的实数根 C、k为任何实数，方程都有两个相等的实数根 D、根据k的取值不同，方程根的情况分为没有实数根、有两个不相等的实数根和有两个相等的实数根三种

查看试题解析

二、认真填一填

11. 请写出一个与- $\sqrt{3}$ 的积为有理数的数是．

查看试题解析
12. 一元二次方程（a﹣1）x²+x+a²﹣1=0一根为0，则a= ．

查看试题解析
13. 一个多边形的每一个内角都是140°，则这个多边形是边形．

查看试题解析
14. 已知（x²+y²）（x²+y²﹣1）=12，则x²+y²的值是．

查看试题解析
15. 若 $\frac{\sqrt{x + 4}}{x - 2}$ 有意义，则x的取值范围是．

查看试题解析
16. 由10块相同的小长方形地砖拼成面积为1.6m²的长方形ABCD（如图），则长方形ABCD的周长为．

查看试题解析

三、全面答一答

17. 计算

(1)、 $\sqrt{8}$ + $\sqrt{32}$ ﹣ $\sqrt{2}$

(2)、（3+ $\sqrt{2}$ ）（3﹣ $\sqrt{2}$ ）+（1+ $\sqrt{2}$ ）² ．

查看试题解析
18. 选择适当的方法解下列方程：

(1)、3x²﹣7x=0

(2)、x²﹣12x﹣4=0．

查看试题解析
19. 八（2）班组织了一次经典朗读比赛，甲、乙两队各10人的比赛成绩如表（10分制）：
甲
7
8
9
7
10
10
9
10
10
10
乙
10
8
7
9
8
10
10
9
10
9

(1)、甲队成绩的中位数是分，乙队成绩的众数是分；

(2)、计算甲、乙队的平均成绩和方差，试说明成绩较为整齐的是哪一队？

查看试题解析
20.
如图，在▱ABCD中，AE、BF分别平分∠DAB和∠ABC，交CD于点E、F，AE、BF相交于点M．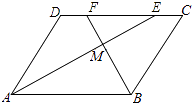

(1)、试说明：AE⊥BF；

(2)、判断线段DF与CE的大小关系，并予以说明．

查看试题解析
21.
水库大坝截面的迎水坡坡比（DE与AE的长度之比）为1：0.6，背水坡坡比为1：2，大坝高DE=30米，坝顶宽CD=10米，求大坝的截面的周长和面积．

查看试题解析
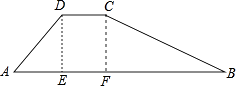22. 随着阿里巴巴、淘宝网、京东、小米等互联网巨头的崛起，催生了快递行业的高速发展．据调查，杭州市某家小型快递公司，今年一月份与三月份完成投递的快递总件数分别为10万件和12.1万件．现假定该公司每月投递的快递总件数的增长率相同．

(1)、求该快递公司投递快递总件数的月平均增长率；

(2)、如果平均每人每月最多可投递快递0.6万件，那么该公司现有的21名快递投递业务员能否完成今年4月份的快递投递任务？如果不能，请问至少需要增加几名业务员？

查看试题解析
23. 已知：关于x的一元二次方程mx²﹣（3m+2）x+2m+2=0（m＞0）

(1)、求证：方程有两个不相等的实数根且其中一根为定值．

(2)、设方程的两个实数根分别为x₁ ， x₂（其中x₁＜x₂）．若y是关于m的函数，且y=7x₁﹣mx₂ ，求这个函数的解析式；并求当自变量m的取值范围满足什么条件时，y≤3m．

查看试题解析

用电量（度）	120	140	160	180	200
户数	2	3	6	7	2

x	5.12	5.13	5.14	5.15
ax²+bx+c	﹣0.04	﹣0.02	0.01	0.03

甲	7	8	9	7	10	10	9	10	10	10
乙	10	8	7	9	8	10	10	9	10	9