2016-2017学年天津市武清区八年级下学期期中数学试卷
试卷更新日期:2017-05-27 类型:期中考试
一、选择题
-
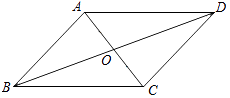
1. 若式子 在实数范围内有意义,则实数a的取值范围是( )A、a>﹣1 B、a≥﹣1 C、a>1 D、a≥12. 下列根式中,不是最简二次根式的是( )A、 B、 C、 D、3. 下列各组数中能作为直角三角形的三边长的是( )A、4,5,6 B、1,1, C、6,8,11 D、5,12,234. 下列计算正确的是( )A、 =2 B、( )2=4 C、 × = D、 ÷ =35. 如图,在▱ABCD中,∠A=3∠B,则∠C的大小是( )
 A、100° B、120° C、135° D、150°6. 如图,在△ABC中,∠ACB=90°,DE垂直平分AC交AB于点E,若BC=6,则DE的长为( )
A、100° B、120° C、135° D、150°6. 如图,在△ABC中,∠ACB=90°,DE垂直平分AC交AB于点E,若BC=6,则DE的长为( )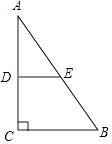 A、6 B、5 C、4 D、37. 菱形具有而一般平行四边形不具有的性质是( )A、对边相等 B、对角相等 C、对角线互相平分 D、对角线互相垂直8. 如图,数轴上点A,B分别对应1,2,过点B作PQ⊥AB,以点B为圆心,AB长为半径画弧,交PQ于点C,以原点O为圆心,OC长为半径画弧,交数轴于点M,则点M对应的数是( )
A、6 B、5 C、4 D、37. 菱形具有而一般平行四边形不具有的性质是( )A、对边相等 B、对角相等 C、对角线互相平分 D、对角线互相垂直8. 如图,数轴上点A,B分别对应1,2,过点B作PQ⊥AB,以点B为圆心,AB长为半径画弧,交PQ于点C,以原点O为圆心,OC长为半径画弧,交数轴于点M,则点M对应的数是( )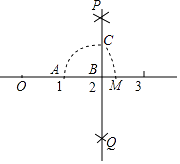 A、 B、 C、 D、9. 下列二次根式:① ;② ;③ ;④ .能与 合并的是( )A、①和(4) B、②和③ C、①和② D、③和④10. 如图,“赵爽弦图”是由四个全等的直角三角形和一个小正方形构成的大正方形,若直角三角形的两直角边长分别为5和3,则小正方形的面积为( )
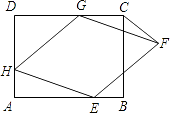
A、 B、 C、 D、9. 下列二次根式:① ;② ;③ ;④ .能与 合并的是( )A、①和(4) B、②和③ C、①和② D、③和④10. 如图,“赵爽弦图”是由四个全等的直角三角形和一个小正方形构成的大正方形,若直角三角形的两直角边长分别为5和3,则小正方形的面积为( ) A、4 B、3 C、2 D、111. 如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )
A、4 B、3 C、2 D、111. 如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )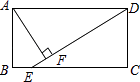 A、△AFD≌△DCE B、AF= AD C、AB=AF D、BE=AD﹣DF12. 如图,以直角三角形a、b、c为边,向外作等边三角形,半圆,等腰直角三角形和正方形,上述四种情况的面积关系满足S1+S2=S3图形个数有( )
A、△AFD≌△DCE B、AF= AD C、AB=AF D、BE=AD﹣DF12. 如图,以直角三角形a、b、c为边,向外作等边三角形,半圆,等腰直角三角形和正方形,上述四种情况的面积关系满足S1+S2=S3图形个数有( )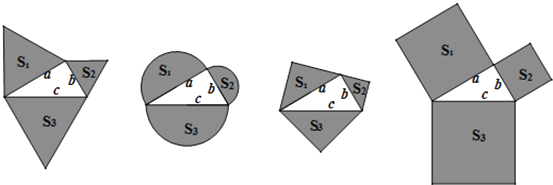 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
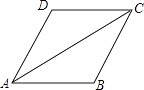
13. 计算: = .14. 直角三角形两直角边长分别为 , ,则斜边长为 .15. 矩形的两条对角线所夹的锐角为60°,较短的边长为12,则对角线长为 .16. 已知n是一个正整数, 是整数,则n的最小值是 .17. 如图,菱形ABCD中,AB=AC=2,点E、F是AB,AD边上的动点,且AE=DF,则EF长的最小值为 .
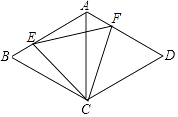 18. 如图,四边形ABCD是正方形,△ABE是等边三角形,EC= ,则正方形ABCD的面积为 .
18. 如图,四边形ABCD是正方形,△ABE是等边三角形,EC= ,则正方形ABCD的面积为 .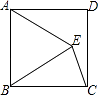
三、解答题
-
19. 计算:(1)、( + )×(2)、(4 ﹣3 )÷2 + .20. 在△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,若c﹣a=4,b=12,求a,c.21. 已知:x2+y2﹣10x+2y+26=0,求( +y)( ﹣y)的值.22. 如图,将长为2.5米长的梯子AB斜靠在墙上,BE长0.7米.
 (1)、求梯子上端到墙的底端E的距离(即AE的长);(2)、如果梯子的顶端A沿墙下滑0.4米(即AC=0.4米),则梯脚B将外移(即BD长)多少米?
(1)、求梯子上端到墙的底端E的距离(即AE的长);(2)、如果梯子的顶端A沿墙下滑0.4米(即AC=0.4米),则梯脚B将外移(即BD长)多少米?