2016-2017学年山西省吕梁市孝义市八年级下学期期中数学试卷

试卷更新日期：2017-05-27 类型：期中考试

进入出卷网下载

一、选择题

1. 下列式子中，属于最简二次根式的是（）

A、 $\sqrt{9}$ B、 $\sqrt{20}$ C、 $\sqrt{7}$ D、 $\sqrt{\frac{1}{3}}$

查看试题解析
2. 若代数式 $\frac{\sqrt{x}}{x - 1}$ 有意义，则实数x的取值范围是（）

A、x≠1 B、x≥0 C、x＞0 D、x≥0且x≠1

查看试题解析
3. 已知x= $\sqrt{3}$ +1，y= $\sqrt{3}$ ﹣1，则代数式 $\sqrt{x^{2} + y^{2}}$ 的值为（）

A、2 $\sqrt{3}$ B、2 $\sqrt{2}$ C、4 D、±2 $\sqrt{2}$

查看试题解析
4. 在平行四边形ABCD 中，∠A：∠B：∠C：∠D的值可以是（）

A、1：2：1：2 B、1：2：2：1 C、1：2：3：4 D、1：1：2：2

查看试题解析
5.
如图字母B所代表的正方形的面积是（　　）

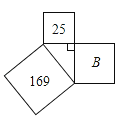A、12 B、13 C、144 D、194

查看试题解析
6.
如图为某楼梯，测得楼梯的长为5米，高3米，计划在楼梯表面铺地毯，地毯的长度至少需要多米？（）

A、4 B、8 C、9 D、7

查看试题解析
7. 下列命题是真命题的是（）

A、一组对边平行，另一组对边相等的四边形是平行四边形 B、对角线互相垂直的平行四边形是矩形 C、四条边相等的四边形是菱形 D、对角线相等的矩形是正方形

查看试题解析
8. 三角形的三边长分别为6，8，10，它的最短边上的高为（）

A、6 B、4.5 C、2.4 D、8

查看试题解析
9. 我们把顺次连接任意一个四边形各边中点所得的四边形叫做中点四边形．如果一个四边形是矩形，那么它的中点四边形是（）

A、平行四边形 B、矩形 C、菱形 D、正方形

查看试题解析
10. 如图，正方形ABCD的边长为4，点E在对角线BD上，且∠BAE=22.5°，EF⊥AB，垂足为点F，则EF的长为（）

A、1 B、4﹣2 $\sqrt{2}$ C、 $\sqrt{2}$ D、3 $\sqrt{2}$ ﹣4

查看试题解析

二、填空题

11. 已知三角形的三边长分别为5，5，6，则该三角形的面积为．

查看试题解析
12. 如图，从一个大正方形中截去面积为32和18的两个小正方形，则大正方形的周长为．

查看试题解析
13. 如图，A、B两点被池塘隔开，在AB外选一点C，连接AC、BC，取AC、BC的中点D、E，量出DE=a，则AB=2a，它的根据是．

查看试题解析
14.
如图四边形ABCD的对角线互相垂直，且OB=OD，请你添加一个适当的条件使它成为菱形（只需添加一个）

查看试题解析
15.
已知，矩形ABCO的对角线AC、BO相交于点D，△ADO是等边三角形，且A点的坐标为（0，2），则点D的坐标为．

查看试题解析
16.
如图，正方形ABCD，AC、BD交于点O，点E、F分别在AB、BC上，且∠EOF=90°，则下列结论①AE=BF，②OE=OF，③BE+BF=AD，④AE²+CF²=2OE²中正确的有（只写序号）

查看试题解析

三、解答题

17. 计算题

(1)、计算： $\sqrt{8}$ +2 $\sqrt{3}$ ﹣（ $\sqrt{27}$ ﹣ $\sqrt{2}$ ）

(2)、计算： $\sqrt{\frac{2}{3}}$ ÷ $\sqrt{2 \frac{2}{3}}$ × $\sqrt{\frac{2}{5}}$

(3)、计算：（3 $\sqrt{2}$ +2 $\sqrt{3}$ ）（3 $\sqrt{2}$ ﹣2 $\sqrt{3}$ ）

查看试题解析
18. 细心观察图，认真分析各式，然后解答问题：
（ $\sqrt{1}$ ）²+1=2，S₁= $\frac{\sqrt{1}}{2}$
（ $\sqrt{2}$ ）²+1=3，S₂= $\frac{\sqrt{2}}{2}$
（ $\sqrt{3}$ ）²+1=4，S₃= $\frac{\sqrt{3}}{2}$

(1)、用含n（n是正整数）的等式表示上述变化规律；

(2)、计算S₁²+S₂²+S₃²+S₄²+…+S₁₀²的值．

查看试题解析
19. 数学活动课上，老师组织学生测量学校旗杆的高度，同学们发现系在旗杆顶端的绳子垂到了地面还多1米，当同学们把绳子的下端拉开5米后，发现绳子下端刚好接触地面，请你根据题意画出图形，并求旗杆的高度．

查看试题解析
20.
如图，将平行四边形ABCD的边AB延长至点E，使BE=AB，连接DE，EC，DE，交BC于点O．

(1)、求证：△ABD≌△BEC；

(2)、连接BD，若∠BOD=2∠A，求证：四边形BECD是矩形．

查看试题解析
21.
如图，在△ABC中，∠BAC=90°，∠ACB=30°，BC=8，以BC为边，在△ABC外作等边△BCD，点E为BC中点，连接AE并延长交CD于点F．

(1)、求证：四边形ABDF是平行四边形；

(2)、如图2，将图1中的ABCD折叠，使点D和点A重合，折痕为GH，求CG的长．

查看试题解析
22.
如图1，在正方形ABCD中，P为对角线BD上的一点，点E在AD的延长线上，且PA=PE，PE交CD于F，连接CE．

(1)、求证：△PCE是等腰直角三角形；

(2)、如图2，把正方形ABCD改为菱形ABCD，其他条件不变，当∠ABC=120°时，判断△PCE的形状，并说明理由．

查看试题解析