2016-2017学年江苏省扬州市江都区五校联谊八年级下学期期中数学试卷

试卷更新日期：2017-05-27 类型：期中考试

进入出卷网下载

一、选择题

1.
下列四张扑克牌中，属于中心对称的图形是（）

A、红桃7 B、方块4 C、梅花6 D、黑桃5

查看试题解析
2. 下列等式成立的是（）

A、 $\frac{1}{a} + \frac{2}{b}$ = $\frac{3}{a + b}$ B、 $\frac{a b}{a b - b^{2}}$ = $\frac{a}{a - b}$ C、 $\frac{2}{2 a + b}$ = $\frac{1}{- a + b}$ D、 $\frac{a}{- a + b}$ =﹣ $\frac{a}{a + b}$

查看试题解析
3. 如果把分式 $\frac{3 n}{m - n}$ 中的m和n都扩大3倍，那么分式的值（）

A、不变 B、扩大3倍 C、缩小3倍 D、扩大9倍

查看试题解析
4. 下列有四种说法：
①了解某一天出入扬州市的人口流量用普查方式最容易；
②“在同一年出生的367名学生中，至少有两人的生日是同一天”是必然事件；
③“打开电视机，正在播放少儿节目”是随机事件；
④如果一件事发生的概率只有十万分之一，那么它仍是可能发生的事件．
其中，正确的说法是（）

A、①②③ B、①②④ C、①③④ D、②③④

查看试题解析
5. 顺次连接下列各四边形中点所得的四边形是矩形的是（）

A、等腰梯形 B、矩形 C、平行四边形 D、菱形或对角线互相垂直的四边形

查看试题解析
6. 如图，E是正方形ABCD的边BC延长线上一点，且CE=AC，则∠E=（）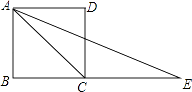

A、90° B、45° C、30° D、22.5°

查看试题解析
7.
如图，在菱形ABCD中，∠BAD=84°，AB的垂直平分线交对角线AC于点F，垂足为E，连接DF，则∠CDF等于（）

A、64° B、54° C、60° D、84°

查看试题解析
8.
如图，正方形ABCD中，点E、F分别在BC、CD上，△AEF是等边三角形，连接AC交EF于G，下列结论：
①BE=DF，②∠DAF=15°，③AC垂直平分EF，④BE+DF=EF，⑤S_△_CEF=2S_△_ABE ．
其中正确结论有（）个．

A、4 B、3 C、2 D、1

查看试题解析

二、填空题

9. 若分式 $\frac{x^{2} - 4}{x - 2}$ 的值为0，则x的值为．

查看试题解析
10. 分式 $\frac{1}{2 x^{3}}$ ， $\frac{1}{6 x^{2} (x - y)}$ 的最简公分母是．

查看试题解析
11. 某电视台综艺节目接到热线电话3000个，现要从中抽取“幸运观众”50名，小明打通了一次热线电话，那么他成为“幸运观众”的概率为．

查看试题解析
12. 如图，在菱形ABCD中，AC、BD相交于点O，E为AB的中点，若OE=2，则菱形ABCD的周长是．

查看试题解析
13. 若分式方程 $\frac{m}{x - 3} = \frac{2}{x - 3} + 1$ 有增根，则m= ．

查看试题解析
14. 如图，△COD是由△AOB绕点O按顺时针方向旋转40°后得到的图形，点C恰好在边AB上．若∠AOD=100°，则∠D的度数是°．

查看试题解析
15. 已知 $\frac{1}{x} - \frac{1}{y} = 3$ ，则代数式 $\frac{2 x - 14 x y - 2 y}{x - 2 x y - y}$ 的值为．

查看试题解析
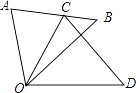16. 关于x的分式方程 $\frac{2 x + m}{x - 3}$ =3解为正数，则m的取值范围是．

查看试题解析
17.
如图，将矩形ABCD绕点C顺时针旋转90°得到矩形FGCE，点M、N分别是BD、GE的中点，若BC=14，CE=2，则MN的长为．

查看试题解析
18.
如图，菱形ABCD的两条对角线分别长6和8，点P是对角线AC上的一个动点，点M、N分别是边AB、BC的中点，则PM+PN的最小值是．

查看试题解析

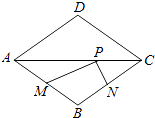
三、解答题

19. 计算：

(1)、 $\frac{a - 2}{a + 1}$ ﹣ $\frac{2 a - 3}{a + 1}$

(2)、（ $\frac{2 x}{x - 3}$ ﹣ $\frac{x}{x + 3}$ ）• $\frac{x^{2} - 9}{x}$ ．

查看试题解析
20. 解下列方程：

(1)、 $\frac{2 x}{x - 2}$ ﹣ $\frac{2}{2 - x}$ =1

(2)、 $\frac{x + 1}{x - 1}$ ﹣ $\frac{4}{x^{2} - 1}$ =1．

查看试题解析
21.
方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，点C的坐标为（4，﹣1）．

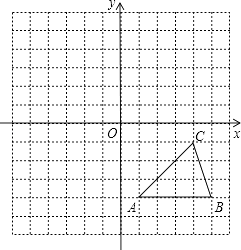(1)、试作出△ABC以C为旋转中心，沿顺时针方向旋转90°后的图形△A₁B₁C；

(2)、以原点O为对称中心，再画出与△ABC关于原点O对称的△A₂B₂C₂ ，并写出点C₂的坐标．

查看试题解析
22. 先化简，再求值：（ $\frac{x + 2}{x^{2} - 2 x}$ ﹣ $\frac{x - 1}{x^{2} - 4 x + 4}$ ）÷ $\frac{x - 4}{x}$ ，其中x²﹣4x﹣1=0．

查看试题解析
23.
学生的学业负担过重会严重影响学生对待学习的态度．为此我市教育部门对部分学校的八年级学生对待学习的态度进行了一次抽样调查（把学习态度分为三个层级，A级：对学习很感兴趣；对学习较感兴趣；对学习不感兴趣），并将调查结果绘制成图①和图②的统计图（不完整）．请根据图中提供的信息，解答下列问题：

(1)、此次抽样调查中，共调查了名学生；

(2)、将图①补充完整；

(3)、求出图②中C级所占的圆心角的度数；

(4)、根据抽样调查结果，请你估计我市近8000名八年级学生中大约有多少名学生学习态度达标（达标包括A级和B级）？

查看试题解析
24.
如图，在▱ABCD中，∠ABC的平分线交AD于点E，延长BE交CD的延长线于F．

(1)、若∠F=40°，求∠A的度数；

(2)、若AB=10，BC=16，CE⊥AD，求▱ABCD的面积．

查看试题解析
25.
已知：如图，在菱形ABCD中，对角线AC、BD相交于点O，DE∥AC，AE∥BD．

(1)、求证：四边形AODE是矩形；

(2)、若AB=4，∠BCD=120°，求四边形AODE的面积．

查看试题解析
26. 某超市规定：凡一次购买大米160kg以上可以按原价打折出售，购买160kg（包括160kg）以下只能按原价出售．小明家到超市买大米，原计划买的大米，只能按原价付款，需要600元；若多买40kg，则按打折价格付款，恰巧需要也是600元．

(1)、求小明家原计划购买大米数量x（千克）的范围；

(2)、若按原价购买4kg与打折价购买5kg的款相同，那么原计划小明家购买多少大米？

查看试题解析
27.
如图1，直角梯形ABCD中，AD∥BC，∠ADC=90°，AD=8，BC=6，点M从点D出发，以每秒2个单位长度的速度向点A运动，同时，点N从点B出发，以每秒1个单位长度的速度向点C运动．其中一个动点到达终点时，另一个动点也随之停止运动．过点N作NP⊥AD于点P，连接AC交NP于点Q，连接MQ．设运动时间为t秒．

(1)、AM= ， AP= ．（用含t的代数式表示）

(2)、当四边形ANCP为平行四边形时，求t的值

(3)、如图2，将△AQM沿AD翻折，得△AKM，是否存在某时刻t，
①使四边形AQMK为为菱形，若存在，求出t的值；若不存在，请说明理由
②使四边形AQMK为正方形，则AC等于．

查看试题解析
28.
已知正方形ABCD中，E为对角线BD上一点，过E点作EF⊥BD交BC于F，连接DF，G为DF中点，连接EG，CG．

(1)、求证：EG=CG；

(2)、将图①中△BEF绕B点逆时针旋转45°，如图②所示，取DF中点G，连接EG，CG．问（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由；

(3)、将图①中△BEF绕B点旋转任意角度，如图③所示，再连接相应的线段，问（1）中的结论是否仍然成立？通过观察你还能得出什么结论（均不要求证明）．

查看试题解析