2016-2017学年江苏省扬州市邗江区八年级下学期期中数学试卷

试卷更新日期：2017-05-27 类型：期中考试

进入出卷网下载

一、选择题

1. 下列事件中，是不可能事件的是（）

A、买一张电影票，座位号是奇数 B、射击运动员射击一次，命中9环 C、明天会下雨 D、度量三角形的内角和，结果是360°

查看试题解析
2. 一次数学测试后，某班40名学生的成绩被分为5组，第1～4组的频数分别为12、10、6、8，则第5组的频率是（）

A、0.1 B、0.2 C、0.3 D、0.4

查看试题解析
3. 为了了解2016年扬州市九年级学生学业水平考试的数学成绩，从中随机抽取了1000名学生的数学成绩．下列说法正确的是（）

A、2016年扬州市九年级学生是总体 B、每一名九年级学生是个体 C、1000名九年级学生是总体的一个样本 D、样本容量是1000

查看试题解析
4.
小敏不慎将一块平行四边形玻璃打碎成如图的四块，为了能在商店配到一块与原来相同的平行四边形玻璃，他带了两块碎玻璃，其编号应该是（）

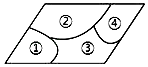A、①，② B、②，③ C、③，④ D、①，④

查看试题解析
5. 菱形具有而平行四边形不具有的性质是（）

A、对角线互相垂直 B、两组对角分别相等 C、对角线互相平分 D、两组对边分别平行

查看试题解析

6. “六•一”儿童节，某玩具超市设立了一个如图所示的可以自由转动的转盘，开展有奖购买活动．顾客购买玩具就能获得一次转动转盘的机会，当转盘停止时，指针落在哪一区域就可以获得相应奖品．下表是该活动的一组统计数据．下列说法不正确的是（）

转动转盘的次数n	100	150	200	500	800	1000
落在“铅笔”区域的次数m	68	108	140	355	560	690
落在“铅笔”区域的频率 $\frac{m}{n}$	0.68	0.72	0.70	0.71	0.70	0.69

A、当n很大时，估计指针落在“铅笔”区域的频率大约是0.70 B、假如你去转动转盘一次，获得铅笔的概率大约是0.70 C、如果转动转盘2000次，指针落在“文具盒”区域的次数大约有600次 D、转动转盘10次，一定有3次获得文具盒

查看试题解析

7.
如图，在正方形ABCD的外侧，作等边三角形ADE，AC、BE相交于点F，则∠BFC为（）

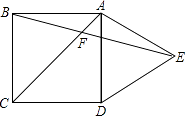A、45° B、55° C、60° D、75°

查看试题解析
8.
如图，将矩形ABCD绕点C顺时针旋转90°得到矩形FGCE，点M、N分别是BD、GE的中点，若BC=14，CE=2，则MN的长（）

A、7 B、8 C、9 D、10

查看试题解析

二、填空题

9. 当x时，分式 $\frac{1}{x - 2}$ 有意义．

查看试题解析
10. 袋子里有5只红球，3只白球，每只球除颜色以外都相同，从中任意摸出1只球，是红球的可能性（选填“大于”“小于”或“等于”）是白球的可能性．

查看试题解析
11. 分式 $\frac{1}{2 x^{3}}$ ， $\frac{1}{6 x^{2} (x - y)}$ 的最简公分母是．

查看试题解析
12.
从1984年起，我国参加了多届夏季奥运会，取得了骄人的成绩．如图是根据第23届至30届夏季奥运会我国获得的金牌数绘制的折线统计图，观察统计图可得：与上一届相比增长量最大的是第届夏季奥运会．

查看试题解析
13.
如图，在Rt△ABC中，∠ACB=90°，D、E、F分别是AB、BC、CA的中点，若CD=3cm，则EF=cm．

查看试题解析
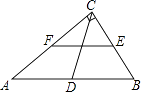14. 如图，四边形ABCD是菱形，AC=8，DB=6，DH⊥AB于点H，则DH= ．

查看试题解析
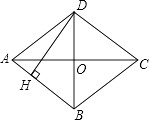15.
如图，E，F，G，H分别是矩形ABCD各边的中点，AB=6，BC=8，则四边形EFGH的面积是．

查看试题解析
16. 已知：如图，平行四边形ABCD中，BE平分∠ABC交AD于E，CF平分∠BCD交AD于F，若AB=3，BC=5，则EF= ．

查看试题解析
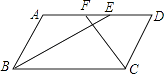17.
如图，在△ABC中，∠ACB=90°，M、N分别是AB、AC的中点，延长BC至点D，使CD= $\frac{1}{3}$ BD，连接DM、DN、MN．若AB=6，则DN= ．

查看试题解析
18.
如图，在菱形ABCD中，AB=6，∠B=60°，点G是边CD边的中点，点E、F分别是AG、AD上的两个动点，则EF+ED的最小值是．

查看试题解析

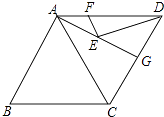
三、解答题

19. 化简：

(1)、 $\frac{1}{x - 3}$ ﹣ $\frac{6}{x^{2} - 9}$

(2)、 $\frac{x^{2} - x}{x^{2} + 2 x + 1}$ ÷ $\frac{x - 1}{x + 1}$ ．

查看试题解析
20. 化简： $(\frac{x}{x - 1} - \frac{1}{x^{2} - x}) \div \frac{x^{2} + 2 x + 1}{x^{2}}$ ，并从﹣1，0，1，2中选择一个合适的数求代数式的值．

查看试题解析
21. 一只不透明的袋子中有2个红球，3个绿球和5个白球，每个球除颜色外都相同，将球搅匀，从中任意摸出一个球．

(1)、会有哪些可能的结果？

(2)、任意摸一个球是绿球的概率是多少？

查看试题解析
22.
如图，在△ABC中，PQ是CA的垂直平分线，CF∥AB交PQ于点F，连接AF．

(1)、求证：△AED≌△CFD；

(2)、求证：四边形AECF是菱形．

查看试题解析
23.
为了解某校九年级学生的身高情况，随机抽取部分学生的身高进行调查，利用所得数据绘成如图统计图表：
频数分布表
身高分组
频数
百分比
x＜155
5
10%
155≤x＜160
a
20%
160≤x＜165
15
30%
165≤x＜170
14
b
x≥170
6
12%
总计

100%

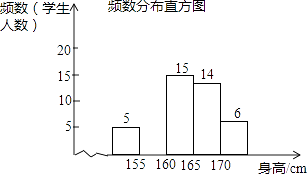(1)、填空：a= ， b=；

(2)、补全频数分布直方图；

(3)、该校九年级共有600名学生，估计身高不低于165cm的学生大约有多少人？

查看试题解析
24.
如图，在正方形网格中，每个小正方形的边长为1个单位长度．平面直角坐标系xOy的原点O在格点上，x轴、y轴都在格线上．线段AB的两个端点也在格点上．

(1)、若将线段AB绕点O逆时针旋转90°得到线段A₁B₁ ，试在图中画出线段A₁B₁ ．

(2)、若线段A₂B₂与线段A₁B₁关于y轴对称，请画出线段A₂B₂ ．

(3)、若点P是此平面直角坐标系内的一点，当点A、B₁、B₂、P四边围成的四边形为平行四边形时，请你直接写出点P的坐标．

查看试题解析
25.
如图，已知Rt△ABC中，∠ABC=90°，先把△ABC绕点B顺时针旋转90°至△DBE后，再把△ABC沿射线AB平移至△FEG，DE、FG相交于点H．

(1)、判断线段DE、FG的位置关系，并说明理由；

(2)、连结CG，求证：四边形CBEG是正方形．

查看试题解析
26. 已知分式M= $\frac{x}{x - 3}$ + $\frac{y}{y - 3}$ ．

(1)、若x=6，y=6，求M的值；

(2)、若x+y=3，xy=2，求M的值？

查看试题解析
27.
如图，在四边形ABCD中，∠ABC=90°，AC=AD，M，N分别为AC，CD的中点，连接BM，MN，BN．

(1)、求证：BM=MN；

(2)、∠BAD=60°，AC平分∠BAD，AC=2，求BN的长．

查看试题解析
28.
如图1，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE．易证：CE=CF．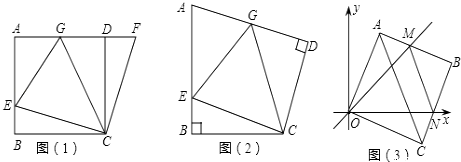

(1)、在图1中，若G在AD上，且∠GCE=45°．试猜想GE，BE，GD三线段之间的数量关系，并证明你的结论．

(2)、运用（1）中解答所积累的经验和知识，完成下面两题：
①如图2，在四边形ABCD中∠B=∠D=90°，BC=CD，点E，点G分别是AB边，AD边上的动点．若∠BCD=α，∠ECG=β，试探索当α和β满足什么关系时，图1中GE，BE，GD三线段之间的关系仍然成立，并说明理由．
②在平面直角坐标中，边长为1的正方形OABC的两顶点A，C分别在y轴、x轴的正半轴上，点O在原点．现将正方形OABC绕O点顺时针旋转，当A点第一次落在直线y=x上时停止旋转，旋转过程中，AB边交直线y=x于点M，BC边交x轴于点N（如图3）．设△MBN的周长为p，在旋转正方形OABC的过程中，p值是否有变化？若不变，请直接写出结论．

查看试题解析

身高分组	频数	百分比
x＜155	5	10%
155≤x＜160	a	20%
160≤x＜165	15	30%
165≤x＜170	14	b
x≥170	6	12%
总计		100%