2016-2017学年江苏省盐城市东台市六校八年级下学期期中数学试卷

试卷更新日期：2017-05-27 类型：期中考试

进入出卷网下载

一、选择题

1.
下列图案中，是中心对称图形的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 在 $\frac{1}{x}$ 、 $\frac{1}{3}$ 、 $\frac{x^{2} + 1}{2}$ 、 $\frac{3 x y}{π}$ 、 $\frac{3}{x + y}$ 、a+ $\frac{b}{5}$ 中，分式的个数有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
3. 下列计算错误的是（）

A、 $\frac{1}{c} + \frac{2}{c} = \frac{3}{c}$ B、 $\frac{a - b}{b - a} = - 1$ C、 $\frac{0.2 a + b}{0.7 a - b} = \frac{2 a + b}{7 a - b}$ D、 $\frac{x^{3} y^{2}}{x^{2} y^{3}} = \frac{x}{y}$

查看试题解析
4. 已知矩形的面积为10，那么它的长y与宽x之间的关系用图象大致可表示为（）

A、 B、 C、 D、

查看试题解析
5. 已知点A（﹣2，y₁），B（2，y₂），C（3，y₃）都在反比例函数y=﹣ $\frac{6}{x}$ 的图象上，则下列结论中正确的是（）

A、y₁＜y₂＜y₃ B、y₃＜y₂＜y₁ C、y₁＜y₃＜y₂ D、y₂＜y₃＜y₁

查看试题解析
6. 在▱ABCD中，如果添加一个条件，就可推出▱ABCD是矩形，那么添加的条件可以是（）

A、AB=BC B、AC=BD C、AC⊥BD D、AB⊥BD

查看试题解析
7. 如图，菱形ABCD的两条对角线相交于O，若AC=8，BD=6，则菱形ABCD的周长是（）

A、32 B、24 C、40 D、20

查看试题解析
8.
如图，在四边形ABCD中，AB∥DC，AD=BC=5，DC=7，AB=13，点P从点A出发以3个单位/s的速度沿AD→DC向终点C运动，同时点Q从点B出发，以1个单位/s的速度沿BA向终点A运动．当四边形PQBC为平行四边形时，运动时间为（　　）

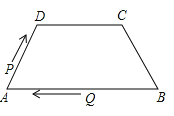A、4s B、3s C、2s D、1s

查看试题解析

二、填空题

9. 使分式 $\frac{x - 1}{x + 3}$ 有意义的x的取值范围是．

查看试题解析
10. 计算： $\frac{2 x}{x - y} + \frac{2 y}{y - x}$ = ．

查看试题解析
11. 要使分式 $\frac{x + 2}{x - 1}$ 的值为0，则x的值为．

查看试题解析
12. 已知双曲线y= $\frac{k + 1}{x}$ 经过点（﹣1，2），那么k的值等于．

查看试题解析
13. 已知反比例函数y= $\frac{1 - 3 m}{x}$ （m为常数）的图象在每个象限内y随x增大而增大，则m的取值范围为．

查看试题解析
14. 若方程 $\frac{x}{x - 4} = 2 + \frac{a}{x - 4}$ 有增根，则a= ．

查看试题解析
15. 甲、乙两地相距48千米，一艘轮船从甲地顺流航行至乙地，又立即从乙地逆流返回甲地，共用时9小时，已知水流的速度为4千米/时，若设该轮船在静水中的速度为x千米/时，则根据题意列出的方程为．

查看试题解析
16.
如图，已知正方形ABCD，点E在边DC上，DE=4，EC=2，则AE的长为．

查看试题解析
17.
如图，已知正方形ABCD的边长为1，连接AC、BD，CE平分∠ACD交BD于点E，则DE= ．

查看试题解析
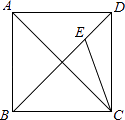18. 如图，在菱形ABCD中，边长为1，∠A=60°，顺次连结菱形ABCD各边中点，可得四边形A₁B₁C₁D₁；顺次连结四边形A₁B₁C₁D₁各边中点，可得四边形A₂B₂C₂D₂；顺次连结四边形A₂B₂C₂D₂各边中点，可得四边形A₃B₃C₃D₃；按此规律继续下去…，则四边形A₂₀₁₆B₂₀₁₆C₂₀₁₆D₂₀₁₆的面积是．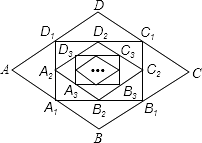

查看试题解析

三、解答题

19. 计算：

(1)、（a²+3a）÷ $\frac{a^{2} - 9}{3 - a}$ ；

(2)、（a+ $\frac{1}{a + 2}$ ）÷（a﹣2+ $\frac{3}{a + 2}$ ）．

(3)、化简求值： $\frac{x^{2} - x}{x^{2} - 2 x + 1}$ •（x﹣ $\frac{1}{x}$ ），其中x= $\frac{1}{5}$ ．

查看试题解析
20. 解分式方程： $\frac{x}{x - 1} - 1 = \frac{2}{x^{2} - 1}$ ．

查看试题解析
21. 在某一电路中，保持电压不变，电流I（安培）与电阻R（欧姆）成反比例，当电阻R=5欧姆时，电流I=2安培．

(1)、求I与R之间的函数关系式；

(2)、当电流I=0.5安培时，求电阻R的值．

查看试题解析
22.
如图，四边形ABCD是平行四边形，点E在BC的延长线上，且CE=BC，AE=AB，AE、DC相交于点O，连接DE．

(1)、求证：四边形ACED是矩形；

(2)、若∠AOD=120°，AC=4，求对角线CD的长．

查看试题解析
23. 某学校开展课外体育活动，决定开设A：篮球、B：乒乓球、C：踢毽子、D：跑步四种活动项目．为了解学生最喜欢哪一种活动项目某中学组织学生到离学校15km的东山游玩，先遣队与大队同时出发，先遣队的速度是大队的速度的1.2倍，结果先遣队比大队早到0.5h，先遣队的速度是多少？大队的速度是多少？

查看试题解析
24. 如图，一次函数y=kx+b的图象与反比例函数y= $\frac{a}{x}$ 的图象相交于A、B两点．

(1)、利用图中条件，求反比例函数和一次函数的解析式；

(2)、根据图象写出使一次函数的值大于反比例函数的值的x的取值范围．

查看试题解析
25.
如图，将矩形ABCD折叠，使点A与点C重合，折痕交BC、AD分别于点E、F．

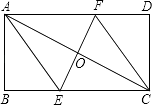(1)、求证：四边形AECF是菱形；

(2)、若AB=4，BC=8，求菱形AECF的面积．

查看试题解析
26.
在正方形ABCD中，点E，F分别在边BC，CD上，且∠EAF=∠CEF=45°．

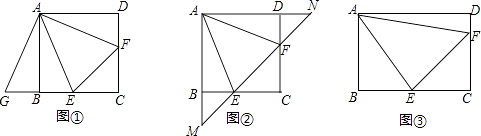(1)、将△ADF绕着点A顺时针旋转90°，得到△ABG（如图①），求证：△AEG≌△AEF；

(2)、若直线EF与AB，AD的延长线分别交于点M，N（如图②），求证：EF²=ME²+NF²；

(3)、将正方形改为长与宽不相等的矩形，若其余条件不变（如图③），请你直接写出线段EF，BE，DF之间的数量关系．

查看试题解析