2016-2017学年江苏省苏州市常熟市八年级下学期期中数学试卷

试卷更新日期：2017-05-27 类型：期中考试

进入出卷网下载

一、选择题

1. 下列调查中，适宜采用普查方式的是（　　）

A、了解一批圆珠笔的寿命 B、了解全国九年级学生身高的现状 C、考察人们保护海洋的意识 D、检查一枚用于发射卫星的运载火箭的各零部件

查看试题解析
2. 如图，将Rt△ABC绕直角顶点C顺时针旋转90°，得到△A′B′C，连接AA′，若∠B=65°，则∠1的度数是（）

A、45° B、25° C、20° D、15°

查看试题解析
3. 如图，将矩形纸片ABCD沿其对角线AC折叠，使点B落到点B′的位置，AB′与CD交于点E，若AB=8，AD=3，则图中阴影部分的周长为（）

A、16 B、19 C、22 D、25

查看试题解析
4. 正方形具有的性质中，菱形不一定具有的性质是（）

A、对角线相等 B、对角线互相垂直 C、对角线互相平分 D、对角线平分一组对角

查看试题解析
5. 一个不透明的盒子中装有10个黑球和若干个白球，它们除颜色不同外，其余均相同．从盒子中随机摸出一球记下其颜色，再把它放回盒子中摇匀，重复上述过程，共试验400次，其中有240次摸到白球．由此估计盒子中的白球大约有（）

A、10个 B、15个 C、18个 D、30个

查看试题解析
6. 已知点（﹣1，y₁），（2，y₂），（π，y₃）在双曲线y= $\frac{k^{2} + 1}{x}$ 图象上，则（）

A、y₁＞y₂＞y₃ B、y₂＞y₃＞y₁ C、y₂＞y₁＞y₃ D、y₃＞y₁＞y₂

查看试题解析
7. 若顺次连接四边形ABCD四边的中点，得到的图形是一个矩形，则四边形ABCD一定是（）

A、矩形 B、菱形 C、对角线相等的四边形 D、对角线互相垂直的四边形

查看试题解析
8.
如图，已知DE是△ABC的一条中位线，F、G分别是线段BD、CE的中点，若DE=4，则FG等于（）

A、5 B、6 C、7 D、8

查看试题解析
9.
已知：如图在直角坐标系中，有菱形OABC，A点的坐标为（10，0），对角线OB、AC相交于D点，双曲线y= $\frac{k}{x}$ （x＞0）经过D点，交BC的延长线于E点，且OB•AC=160，则点E的坐标为（）

A、（5，8） B、（5，10） C、（4，8） D、（3，10）

查看试题解析
10.
如图，正方形ABCD中，AB=6，点E在边CD上，且CD=3DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连结AG、CF．下列结论：①△ABG≌△AFG；②∠EAG=45°；③BG=GC；④AG∥CF．其中正确结论的个数是（）

A、4 B、3 C、2 D、1

查看试题解析

二、填空题：

11. 为了调查滨湖区八年级学生期末考试数学试卷答题情况，从全区的数学试卷中随机抽取了10本没拆封的试卷作为样本，每本含试卷30份，这次抽样调查的样本容量是．

查看试题解析
12. 一个样本的50个数据分别落在5个组内，第1、2、3、4组数据的个数分别是2、8、15、5，则第5组数据的频数为，频率为．

查看试题解析
13. 如图，矩形ABCD中，AC、BD交于点O，∠AOB=60°，DE平分∠ADC交BC于点E，连接OE，则∠COE= ．

查看试题解析
14.
如图，在△ABC中，AB=3，AC=4，BC=5，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为EF中点，则AM的最小值为．

查看试题解析
15.
如图，菱形ABCD的顶点C与原点O重合，点B在y轴的正半轴上，点A在反比例函数y= $\frac{k}{x}$ （k＞0，x＞0）的图象上，点D的坐标为（4，3）．则k的值为．

查看试题解析
16. 矩形ABCD中，AB=3，BC=4，点E是BC边上的一点，连接AE，把∠B沿AE折叠，使点B落在点B'处，当△CEB′为直角三角形时，BE的长为．

查看试题解析
17. 如图，平行四边形ABCD中，点E、F分别在AD、AB上，依次连接EB、EC、FC、FD，图中阴影部分的面积分别为S₁、S₂、S₃、S₄ ，已知S₁=2、S₂=12、S₃=3，则S₄的值是．

查看试题解析
18.
如图，点A是反比例函数 $y = - \frac{2}{x}$ 在第二象限内图象上一点，点B是反比例函数 $y = \frac{4}{x}$ 在第一象限内图象上一点，直线AB与y轴交于点C，且AC=BC，连接OA、OB，则△AOB的面积是．

查看试题解析

三、解答题：

19. 一只不透明的袋子中，装有2个白球、3个黄球和4个红球，这些球除颜色外都相同，将球摇匀，从中任意摸出1个球．

(1)、能事先确定摸到的这个球的颜色吗？

(2)、你认为摸到哪种颜色的球的概率最大？

(3)、怎样改变袋子中白球、黄球、红球的个数，使摸到这这三种颜色的球的概率相等？

查看试题解析
20. 近视眼镜的度数y（度）与镜片焦距x（米）成反比例．已知200度的近视眼镜镜片的焦距为0.5米．求：

(1)、y关于x的函数解析式；

(2)、300度近视眼镜镜片的焦距．

查看试题解析
21.
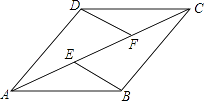
已知：如图，在四边形ABCD中，AB∥CD，E，F为对角线AC上两点，且AE=CF，DF∥BE．
求证：四边形ABCD为平行四边形．

查看试题解析
22.
为迎接常熟市文明城市创建工作，某校八年级一班开展了“社会主义核心价值观、未成年人基本文明礼仪规范”的知识竞赛活动，成绩分为A、B、C、D四个等级，并将收集的数据绘制了两幅不完整的统计图．请你根据图中所给出的信息，解答下列各题：

(1)、求八年级一班共有多少人；

(2)、补全折线统计图；

(3)、在扇形统计图中等极为“D”的部分所占圆心角的度数为；

(4)、若等级A为优秀，求该班的优秀率．

查看试题解析
23.
如图，在平面直角坐标系中，△ABC和△A₁B₁C₁关于点D成中心对称．

(1)、画出对称中心D，并写出点D的坐标；

(2)、画出△A₁B₁C₁绕点O逆时针旋转90°后的△A₂B₂C₂；

(3)、画出与△A₁B₁C₁关于点O成中心对称的△A₃B₃C₃；

(4)、请直接写出△A₃B₃C₃的面积．

查看试题解析
24. 如图，菱形ABCD的对角线交于点O，AC=16cm，BD=12cm．

(1)、求菱形的边长和面积；

(2)、求菱形的高DM．

查看试题解析
25.
如图，在一正方形ABCD中．E为对角线AC上一点，连接EB、ED，

(1)、求证：△BEC≌△DEC：

(2)、延长BE交AD于点F，若∠DEB=140°．求∠AFE的度数．

查看试题解析
26.
平行四边形ABCD中，对角线AC，BD相交于点O，若E、F是AC上两动点，E、F分别从A、C两点同时以2cm/s的相同的速度向C、A运动

(1)、四边形DEBF是平行四边形吗？说明你的理由．

(2)、若BD=10cm，AC=18cm，当运动时间t为多少时，以D、E、B、F为顶点的四边形为矩形．

查看试题解析
27.
平面直角坐标系xOy中，点A、B分别在函数y₁= $\frac{3}{x}$ （x＞0）与y₂=﹣ $\frac{3}{x}$ （x＜0）的图象上，A、B的横坐标分别为a、b．

(1)、若AB∥x轴，求△OAB的面积；

(2)、若△OAB是以AB为底边的等腰三角形，且a+b≠0，求ab的值；

(3)、作边长为2的正方形ACDE，使AC∥x轴，点D在点A的左上方，那么，对大于或等于3的任意实数a，CD边与函数y₁= $\frac{3}{x}$ （x＞0）的图象都有交点，请说明理由．

查看试题解析
28.
如图，在平面直角坐标系中有Rt△ABC，∠BAC=90°，AB=AC，A（﹣3，0），B（0，1），C（m，n）．

(1)、请直接写出C点坐标．

(2)、将△ABC沿x轴的正方向平移t个单位，B′、C′两点的对应点、正好落在反比例函数y= $\frac{k}{x}$ 在第一象限内图象上．请求出t，k的值．

(3)、在（2）的条件下，问是否存x轴上的点M和反比例函数y= $\frac{k}{x}$ 图象上的点N，使得以B′、C′，M，N为顶点的四边形构成平行四边形？如果存在，请求出所有满足条件的点M和点N的坐标；如果不存在，请说明理由．

查看试题解析