2016-2017学年河南省信阳市罗山县八年级下学期期中数学试卷

试卷更新日期：2017-05-27 类型：期中考试

进入出卷网下载

一、选择题

1. 下列二次根式中属于最简二次根式的是（）

A、 $\sqrt{24}$ B、 $\sqrt{36}$ C、 $\sqrt{11}$ D、 $\sqrt{20}$

查看试题解析
2. 下列计算正确的是（）

A、2 $\sqrt{3}$ +3 $\sqrt{2}$ =5 $\sqrt{3}$ B、 $\sqrt{8} \div \sqrt{2}$ =2 C、5 $\sqrt{3} \times$ 5 $\sqrt{2}$ =5 $\sqrt{6}$ D、 $\sqrt{{(- 6)}^{2}}$ =﹣6

查看试题解析
3. 已知（x﹣y+3）²+ $\sqrt{2 x + y}$ =0，则x+y的值为（）

A、0 B、﹣1 C、1 D、5

查看试题解析
4. 顺次连接矩形的四边形中点所得的四边形一定是（）

A、平行四边形 B、矩形 C、菱形 D、正方形

查看试题解析
5. 已知△ABC的三边分别为a．b、c，则下列条件中不能判定△ABC是直角三角形的是（）

A、b²=a²﹣c² B、 $a ： b ： c = 1 ： \sqrt{3} ： 2$ C、∠C=∠A﹣∠B D、∠A：∠B：∠C=3：4：5

查看试题解析
6.
如图，▱ABCD中，对角线AC和BD相交于点O，如果AC=12、BD=10、AB=m，那么m的取值范围是（）

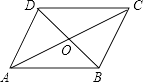A、1＜m＜11 B、2＜m＜22 C、10＜m＜12 D、5＜m＜6

查看试题解析
7. 如图，小明将一张长为20cm，宽为15cm的长方形纸（AE＞DE）剪去了一角，量得AB=3cm，CD=4cm，则剪去的直角三角形的斜边长为（）

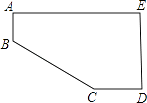A、5cm B、12cm C、16cm D、20cm

查看试题解析
8.
如图，在菱形ABCD中，∠BAD=80°，AB的垂直平分线交对角线AC于点F，垂足为E，连接DF，则∠CDF等于（）

A、50° B、60° C、70° D、80°

查看试题解析
9.
如图，透明的圆柱形容器（容器厚度忽略不计）的高为12cm，底面周长为10cm，在容器内壁离容器底部3cm的点B处有一饭粒，此时一只蚂蚁正好在容器外壁，且离容器上沿3cm的点A处，则蚂蚁吃到饭粒需爬行的最短路径是（）

A、13cm B、2 $\sqrt{61}$ cm C、 $\sqrt{61}$ cm D、2 $\sqrt{34}$ cm

查看试题解析
10.
如图，正方形ABCD中，点E、F分别在BC、CD上，△AEF是等边三角形，连接AC交EF于G，下列结论：①BE=DF，②∠DAF=15°，③AC垂直平分EF，④S_△_CEF=2S_△_ABE ，其中正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 使式子 $\frac{\sqrt{x + 1}}{x - 1}$ 有意义的x的取值范围是．

查看试题解析
12. 矩形的两条对角线所夹的锐角为60°，较短的边长为12，则对角线长为．

查看试题解析
13. 如图，在菱形ABCD中，对角线AC=6，BD=8，点E、F分别是边AB、BC的中点，点P在AC上运动，在运动过程中，存在PE+PF的最小值，则这个最小值是

查看试题解析
14. 如图，把两块相同的含30°角的三角尺如图放置，若 $A D = 6 \sqrt{6}$ cm，则三角尺的最长边长为．

查看试题解析
15. 如图，矩形ABCD中，AB=3，BC=4，点E是BC边上一点，连接AE，把∠B沿AE折叠，使点B落在点B′处．当△CEB′为直角三角形时，BE的长为．

查看试题解析

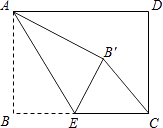
三、解答题

16. 计算：

(1)、3 $\sqrt{3}$ ﹣ $\sqrt{8}$ + $\sqrt{2}$ ﹣ $\sqrt{27}$

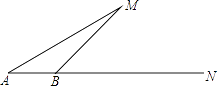
(2)、（ $\sqrt{\frac{1}{2}}$ ﹣ $\sqrt{\frac{1}{3}}$ ）﹣（ $\sqrt{4.5}$ ﹣ $\sqrt{0.75}$ ）

查看试题解析
17. 先化简，再求值： $\frac{a^{2} - 2 a b + b^{2}}{a^{2} - b^{2}} \div (\frac{1}{a} - \frac{1}{b})$ ，其中a= $\sqrt{2}$ +1，b= $\sqrt{2}$ ﹣1．

查看试题解析
18. 有一次，小明坐着轮船由A点出发沿正东方向AN航行，在A点望湖中小岛M，测得∠MAN=30°，航行100米到达B点时，测得∠MBN=45°，你能算出A点与湖中小岛M的距离吗？

查看试题解析
19. 如图，在△ABC中，AB=BC，BD平分∠ABC．四边形ABED是平行四边形，DE交BC于点F，连接CE．
求证：四边形BECD是矩形．

查看试题解析
20.
图，在菱形ABCD中，AB=2，∠DAB=60°，点E是AD边的中点．点M是AB边上一动点（不与点A重合），延长ME交射线CD于点N，连接MD、AN．

(1)、求证：四边形AMDN是平行四边形；

(2)、填空：①当AM的值为时，四边形AMDN是矩形；
②当AM的值为时，四边形AMDN是菱形．

查看试题解析
21.
在某市外郊一段限速公路BC上（公路视为直线），交通管理部门规定汽车的最高行驶速度不能超过60千米/时，并在离该公路100米处设置了一个监测点A，在如图所示的平面直角坐标系中，点A位于y轴上，测速路段BC在x轴上，点B在A的北偏西60°方向上，点C在点A的北偏东45°方向上，另外一条高等级公路在y轴上，OA为其中一段．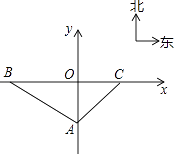

(1)、求点B和C的坐标．

(2)、一辆汽车从点B匀速行驶到点C所用时间为15秒．请你通过计算，判断该汽车在这段限速路上是否超速？（参考数据： $\sqrt{3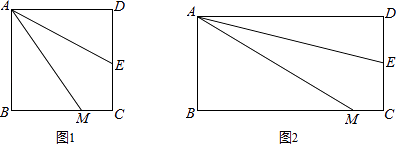} \approx 1.7 ， \sqrt{2} \approx 1.4$ ）

查看试题解析
22.
探究题
【问题情境】
如图1，四边形ABCD是正方形，M是BC边上的一点，E是CD边的中点，AE平分∠DAM．

(1)、【探究展示】

直接写出AM、AD、MC三条线段的数量关系：；

(2)、【拓展延伸】

AM=DE+BM是否成立？若成立，请给出证明；若不成立，请说明理由．

(3)、若四边形ABCD是长与宽不相等的矩形，其他条件不变，如图2，探究展示（1）、（2）中的结论是否成立？请分别作出判断，不需要证明．

查看试题解析
23.
如图，△ABC中，点O为AC边上的一个动点，过点O作直线MN∥BC，设MN交∠BCA的外角平分线CF于点F，交∠ACB内角平分线CE于E．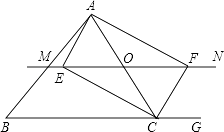

(1)、试说明EO=FO；

(2)、当点O运动到何处时，四边形AECF是矩形并证明你的结论；

(3)、若AC边上存在点O，使四边形AECF是正方形，猜想△ABC的形状并证明你的结论．

查看试题解析