深圳专版2018-2019学年八年级下学期数学期末模拟卷
试卷更新日期:2019-06-11 类型:期末考试
一、选择题
-
1. 如图所示,a∥b,直线a与直线b之间的距离是( )
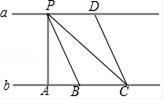 A、线段PA的长度 B、线段PB的长度 C、线段PC的长度 D、线段CD的长度2. 下列式子(1)7>4 (2)3x≥2x+1 (3)x+y>1 (4)x2+3>2x中是一元一次不等式的有( )A、1个 B、2个 C、3个 D、4个3. 下列关于x的方程是分式方程的是( )A、 =1- B、 =2+x C、 + =1 D、 =14. 若 ,则 的值为( )A、3 B、6 C、9 D、125. 如图,函数y=kx+b(k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A,则不等式0<kx+b<2x的解集为( )
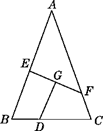
A、线段PA的长度 B、线段PB的长度 C、线段PC的长度 D、线段CD的长度2. 下列式子(1)7>4 (2)3x≥2x+1 (3)x+y>1 (4)x2+3>2x中是一元一次不等式的有( )A、1个 B、2个 C、3个 D、4个3. 下列关于x的方程是分式方程的是( )A、 =1- B、 =2+x C、 + =1 D、 =14. 若 ,则 的值为( )A、3 B、6 C、9 D、125. 如图,函数y=kx+b(k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A,则不等式0<kx+b<2x的解集为( ) A、1<x<2 B、x>2 C、x>0 D、0<x<16. 如图,△ABC中,∠BAC=60°,∠BAC的平分线AD与边BC的垂直平分线MD相交于点D,DE⊥AB交AB的延长线于点E,DF⊥AC于点F,现有下列结论:①DE=DF; ②DE+DF=AD; ③DM平分∠EDF:④AB+AC=2AE.其中正确的有( )
A、1<x<2 B、x>2 C、x>0 D、0<x<16. 如图,△ABC中,∠BAC=60°,∠BAC的平分线AD与边BC的垂直平分线MD相交于点D,DE⊥AB交AB的延长线于点E,DF⊥AC于点F,现有下列结论:①DE=DF; ②DE+DF=AD; ③DM平分∠EDF:④AB+AC=2AE.其中正确的有( )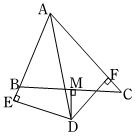 A、1个 B、2个 C、3个 D、4个7.
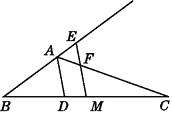
A、1个 B、2个 C、3个 D、4个7.如图,将周长为8的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为( )
 A、6 B、8 C、10 D、128. 如图,▱ABCD中,BC=BD,∠C=74°,则∠ADB的度数是( )
A、6 B、8 C、10 D、128. 如图,▱ABCD中,BC=BD,∠C=74°,则∠ADB的度数是( ) A、16° B、22° C、32° D、68°9. 如图,香港特别行政区标志紫荆花图案绕中心旋转n°后能与原来的图案互相重合,则n的最小值为( )
A、16° B、22° C、32° D、68°9. 如图,香港特别行政区标志紫荆花图案绕中心旋转n°后能与原来的图案互相重合,则n的最小值为( ) A、45 B、60 C、72 D、14410. 下列图形中,不是中心对称图形的是( )A、
A、45 B、60 C、72 D、14410. 下列图形中,不是中心对称图形的是( )A、 B、
B、 C、
C、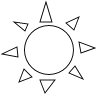 D、
D、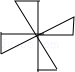 11. 如果a﹣b= ,那么代数式(a﹣ )• 的值是( )A、﹣2 B、2 C、﹣
11. 如果a﹣b= ,那么代数式(a﹣ )• 的值是( )A、﹣2 B、2 C、﹣ D、
D、 12. 若关于x的一元一次不等式组 的解集是x>3,则m的取值范围是( )A、m>4 B、m≥4 C、m<4 D、m≤4
12. 若关于x的一元一次不等式组 的解集是x>3,则m的取值范围是( )A、m>4 B、m≥4 C、m<4 D、m≤4二、填空题
-
13. 多项式x2+mx+5因式分解得(x+5)(x+n),则m= , n= .14. 化简; ÷( ﹣1)= .
15. 线段AB是由线段CD平移得到,点A(﹣2,1)的对应点为C(1,1),则点B(3,2)的对应点D的坐标是 .16. 如图,在△ABC中,AB=4,将△ABC绕点B按逆时针方向旋转30°后得到△A1BC1 , 则阴影部分的面积为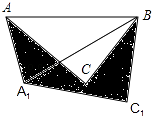
三、解答题
-
17.(1)、化简:(2﹣ )÷(2)、解不等式组:﹣3≤ <518. 对于二次三项式3x2﹣6x+4的值,小明同学作出如下结论:“无论x取任何实数都不可能等于1.”你同意他的说法吗?并说明你的理由.19. 某市一种出租车起步价是5元(路程在3km以内均付5元),达到或超过3km,每增加0.5km加价0.7元(不足0.5km按0.5km计).某乘客坐这种出租车从甲地到乙地,下车时付车费14.8元,那么甲地到乙地的路程是多少?20. 如图,点B、F、C、E在一条直线上,FB=CE,AB∥ED,AC∥FD,AD交BE于O.求证:AD与BE互相平分.
 21. 某修理厂需要购进甲、乙两种配件,经调查,每个甲种配件的价格比每个乙种配件的价格少0.4万元,且用16万元购买的甲种配件的数量与用24万元购买的乙种配件的数量相同.(1)、求每个甲种配件、每个乙种配件的价格分别为多少万元;(2)、现投入资金80万元,根据维修需要预测,甲种配件要比乙种配件至少要多22件,问乙种配件最多可购买多少件.
21. 某修理厂需要购进甲、乙两种配件,经调查,每个甲种配件的价格比每个乙种配件的价格少0.4万元,且用16万元购买的甲种配件的数量与用24万元购买的乙种配件的数量相同.(1)、求每个甲种配件、每个乙种配件的价格分别为多少万元;(2)、现投入资金80万元,根据维修需要预测,甲种配件要比乙种配件至少要多22件,问乙种配件最多可购买多少件.